Lý thuyết Một số phép tính về căn bậc hai của số thực (Cánh diều 2024)

Lý thuyết Một số phép tính về căn bậc hai của số thực (Cánh diều 2024) | Lý thuyết Toán 9

Nguyễn Mạnh Tài Ngày: 08-08-2024 Lớp 9

134

Với tóm tắt lý thuyết Toán lớp 9 Bài 2: Một số phép tính về căn bậc hai của số thực sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực

A. Lý thuyết Một số phép tính về căn bậc hai của số thực

1. Căn bậc hai của một bình phương

Với mọi số a, ta có: $\sqrt{a^{2}} = | a |$ .

Ví dụ:

$\sqrt{13^{2}} = | 13 | = 13$ ; $\sqrt{{(- 8)}^{2}} = | - 8 | = 8$ .

2. Căn bậc hai của một tích

Với hai số không âm a, b, ta có: $\sqrt{a . b} = \sqrt{a} . \sqrt{b}$ .

Chú ý: Quy tắc trên có thể mở rộng cho tích có nhiều thừa số không âm.

Ví dụ:

$\sqrt{81.49} = \sqrt{81} . \sqrt{49} = 9.7 = 63$ ;

$\sqrt{1, 3} . \sqrt{10} . \sqrt{13} = \sqrt{1, 3.10.13} = \sqrt{13.13} = \sqrt{13^{2}} = 13$ .

3. Căn bậc hai của một thương

Với $a \geq 0; b > 0$ , ta có: $\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$ .

Ví dụ:

$\sqrt{\frac{4}{25}} = \frac{\sqrt{4}}{\sqrt{25}} = \frac{2}{5}$ ;

$\frac{\sqrt{216}}{\sqrt{6}} = \sqrt{\frac{216}{6}} = \sqrt{36} = 6$ .
4. Đưa thừa số ra ngoài dấu căn bậc hai

Phép đưa thừa số ra ngoài dấu căn bậc hai

Cho hai số a, b với $b \geq 0$ . Khi đó $\sqrt{a^{2} b} = | a | \sqrt{b}$ .

Cụ thể, ta có:

- Nếu $a \geq 0$ thì $\sqrt{a^{2} b} = a \sqrt{b}$ .

- Nếu $a < 0$ thì $\sqrt{a^{2} b} = - a \sqrt{b}$ .

Ví dụ:

$\sqrt{7^{2} .2} = 7 \sqrt{2}$ ;

$\sqrt{{(- 11)}^{2} .3} = | - 11 | . \sqrt{3} = 11 \sqrt{3}$ .

5. Đưa thừa số vào trong dấu căn bậc hai

Phép đưa thừa số vào trong dấu căn bậc hai

- Với $a \geq 0$ và $b \geq 0$ , ta có: $a \sqrt{b} = \sqrt{a^{2} b}$ .

- Với $a < 0$ và $b \geq 0$ , ta có: $a \sqrt{b} = - \sqrt{a^{2} b}$ .

Ví dụ:

$2 \sqrt{\frac{1}{2}} = \sqrt{2^{2} . \frac{1}{2}} = \sqrt{2}$ ;

$4 \sqrt{\frac{7}{4}} - \sqrt{28} = \sqrt{4^{2} . \frac{7}{4}} - \sqrt{28} = \sqrt{4.7} - \sqrt{28} = \sqrt{28} - \sqrt{28} = 0$ .

Sơ đồ tư duy Một số phép tính về căn bậc hai của số thực

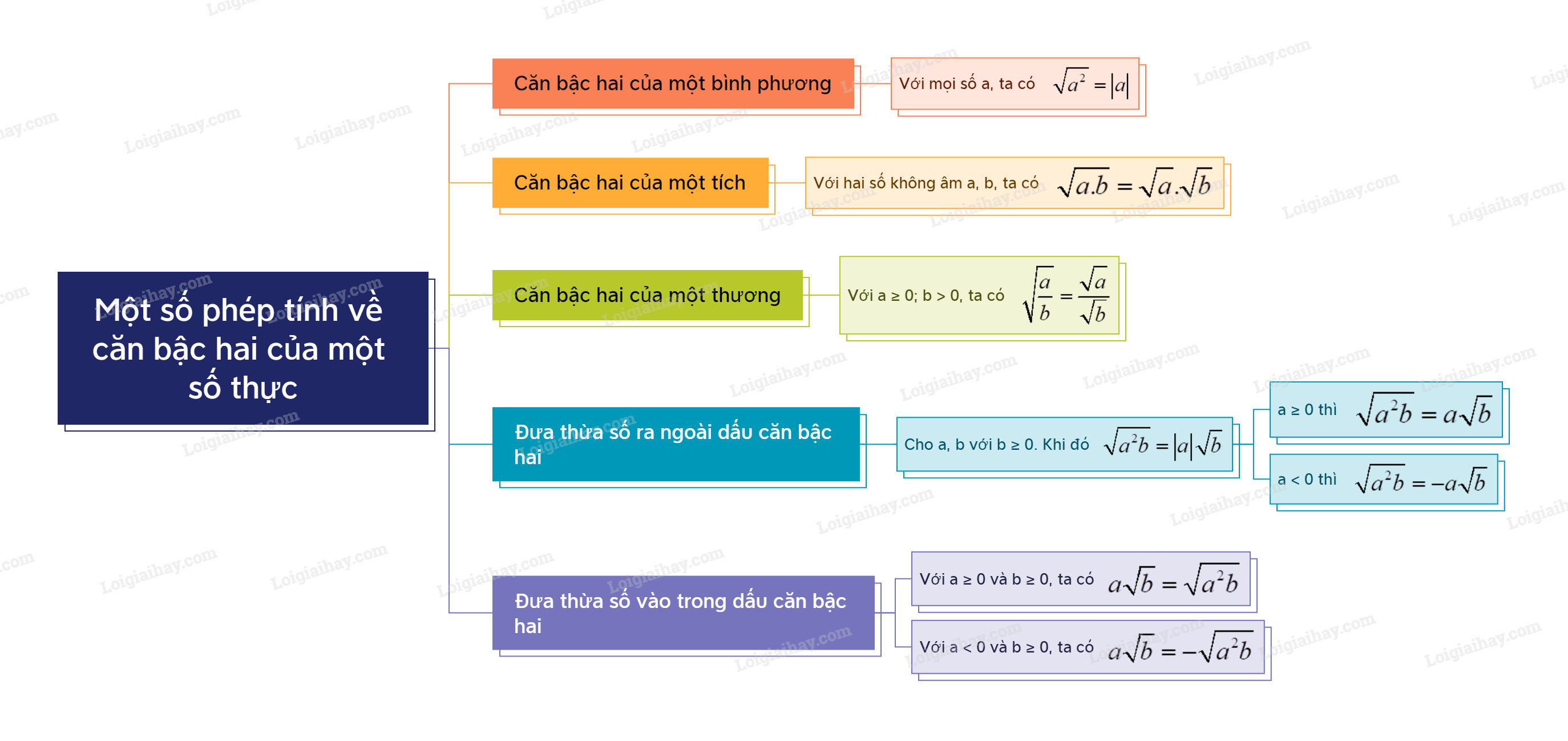
B. Bài tập Một số phép tính về căn bậc hai của số thực

Bài 1.Cho a và b là hai số. Khẳng định nào sau đây là đúng?

A. $a \sqrt{b} = \sqrt{a^{2} b}$ với mọi a, b;

B. $\sqrt{a^{2}} = - a$ khi a < 0;

C. $\sqrt{a b^{2}} = - b \sqrt{a}$ khi a ≥ 0 và b ≥ 0;

D. $\sqrt{- a b} = - \sqrt{a} \cdot \sqrt{b}$ khi a ≥ 0 và b ≥ 0.

Hướng dẫn giải

Đáp án đúng là: B

Ta có:

⦁ $\sqrt{a^{2}} = - a$ khi a < 0;

⦁ $a \sqrt{b} = \sqrt{a^{2} b}$ khi a ≥ 0 và b ≥ 0;

⦁ $\sqrt{a b^{2}} = - b \sqrt{a}$ khi a ≥ 0 và b < 0;

⦁ $\sqrt{- a b} = \sqrt{- a} \cdot \sqrt{b}$ khi a < 0 và b ≥ 0 hoặc $\sqrt{- a b} = \sqrt{a} \cdot \sqrt{- b}$ khi a ≥ 0 và b < 0.

Vậy ta chọn phương án B.

Bài 2. Cho a, b là hai số và b ≠ 0. Rút gọn biểu thức ta được

A. $\frac{a^{2}}{b};$

B. $\frac{a}{b};$

C. $- \frac{a^{2}}{b};$

D. $\frac{a^{2}}{(b)} .$

Hướng dẫn giải

Đáp án đúng là: D

Ta có: $\sqrt{\frac{a^{4}}{b^{2}}} = \sqrt{{(\frac{a^{2}}{b})}^{2}} = (\frac{a^{2}}{b}) = \frac{a^{2}}{(b)} .$

Bài 3. Cho ba số dương a, b, c. Khẳng định nào sau đây là đúng?

A. $\sqrt{\frac{a}{b c}} = \frac{\sqrt{a b c}}{b};$

B. $\sqrt{\frac{a}{b c}} = - \frac{\sqrt{a b c}}{b c};$

C. $\sqrt{\frac{a}{b c}} = \frac{\sqrt{a b c}}{b c};$

D. $\sqrt{\frac{a}{b c}} = \frac{a b c}{\sqrt{b c}} .$

Hướng dẫn giải

Đáp án đúng là: C

Với a > 0, b > 0, c > 0, ta có:

$\sqrt{\frac{a}{b c}} = \sqrt{\frac{a b c}{{(b c)}^{2}}} = \frac{\sqrt{a b c}}{\sqrt{{(b c)}^{2}}} = \frac{\sqrt{a b c}}{|b c|} = \frac{\sqrt{a b c}}{b c} .$

Vậy ta chọn phương án C.

Bài 4. So sánh:

a) $\frac{\sqrt{49}}{\sqrt{7}}$ và 3;

b) $\sqrt{\frac{1}{2}} . \sqrt{\frac{9}{2}}$ và $\frac{3}{2};$

c) $\sqrt{50}$ và $5 \sqrt{5}$

Hướng dẫn giải

a) Ta có: $\frac{\sqrt{49}}{\sqrt{7}} = \sqrt{\frac{49}{7}} = \sqrt{7}$

Vì $\sqrt{7} < \sqrt{9}$ hay $\sqrt{7} < 3$ nên $\frac{\sqrt{49}}{\sqrt{7}} < 3.$

b) Ta có: $\sqrt{\frac{1}{2}} \cdot \sqrt{\frac{9}{2}} = \sqrt{\frac{1}{2} \cdot \frac{9}{2}} = \sqrt{\frac{9}{4}} = \frac{3}{2} .$

c) Ta có: $\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{5^{2} \cdot 2} = 5 \sqrt{2} .$

Vì $\sqrt{2} < \sqrt{5}$ nên $5 \sqrt{2} < 5 \sqrt{5} .$

Vậy $\sqrt{50} < 5 \sqrt{5} .$

Bài 5. Tính:

a) $\sqrt{7 - 4 \sqrt{3}};$

b) $\sqrt{\sqrt{5} + 3} \cdot \sqrt{3 - \sqrt{5}};$

c) $\frac{\sqrt{{(6, 2)}^{2} - {(5, 9)}^{2}}}{\sqrt{2, 43}};$

d) ${(\sqrt{6} - \sqrt{5})}^{2} + \sqrt{120} .$

Hướng dẫn giải

a) $\sqrt{7 - 4 \sqrt{3}} = \sqrt{4 - 2 \cdot 2 \cdot \sqrt{3} + 3} = \sqrt{2^{2} - 2 \cdot 2 \cdot \sqrt{3} + {(\sqrt{3})}^{2}}$

$= \sqrt{{(2 - \sqrt{3})}^{2}} = |2 - \sqrt{3}| = 2 - \sqrt{3}$ (vì $2 - \sqrt{3} > 0$ > do $2 > \sqrt{3}) .$

/span>

b) $\sqrt{\sqrt{5} + 3} \cdot \sqrt{3 - \sqrt{5}} = \sqrt{(3 + \sqrt{5}) (3 - \sqrt{5})}$

$= \sqrt{3^{2} - {(\sqrt{5})}^{2}} = \sqrt{9 - 5} = \sqrt{4} = 2.$

c) $\frac{\sqrt{{(6, 2)}^{2} - {(5, 9)}^{2}}}{\sqrt{2, 43}} = \frac{\sqrt{(6, 2 - 5, 9) \cdot (6, 2 + 5, 9)}}{\sqrt{2, 43}}$

$= \frac{\sqrt{0, 3 \cdot 12, 1}}{\sqrt{2, 43}} = \frac{\sqrt{3, 63}}{\sqrt{2, 43}} = \sqrt{\frac{3, 63}{2, 43}} = \sqrt{\frac{363}{243}} = \sqrt{\frac{121}{81}} = \frac{11}{9} .$