Với tóm tắt lý thuyết Toán lớp 9 Bài 1: Tỉ số lượng giác của góc nhọn sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.
Lý thuyết Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn
A. Lý thuyết Tỉ số lượng giác của góc nhọn
1. Tỉ số lượng giác của một góc nhọn
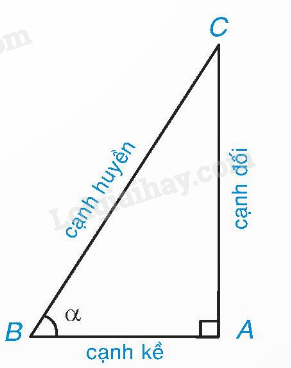
|
. gọi là các tỉ số lượng giác của góc nhọn . |
Tip học thuộc nhanh:
|
Sin đi học Cos không hư Tan đoàn kết Cotang kết đoàn |
Ví dụ:
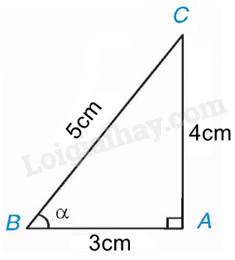
Theo định nghĩa của tỉ số lượng giác, ta có:
, , ,
2. Tỉ số lượng giác của hai góc phụ nhau
Nhận xét: Hai góc nhọn có tổng bằng được gọi là hai góc phụ nhau.
Định lí về tỉ số lượng giác của hai góc phụ nhau
|
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia. Với , ta có: ; ; ; . |
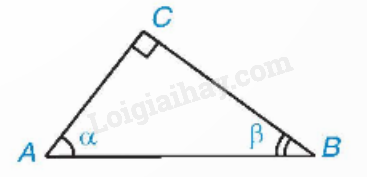
Cho và là hai góc phụ nhau, ta có:
, , , .
Ví dụ:
Bảng giá trị lượng giác của các góc
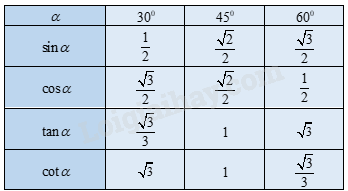
Quy ước:
3. Sử dụng máy tính cầm tay tính tỉ số lượng giác của một góc nhọn
Người ta thường dùng các đơn vị số đo góc là độ (kí hiệu: ), phút (kí hiệu: ), giây (kí hiệu: ).
Ta có thể sử dụng nhiều loại máy tính cầm tay để tính các tỉ số lượng giác của góc nhọn và tính số đo của góc nhọn khi biết một tỉ số lượng giác của nó.
Lưu ý: ta cần đổi đơn vị đo về độ.

Tính các tỉ số lượng giác của các góc nhọn
Để tính tỉ số lượng giác của một góc , ta dùng các nút:
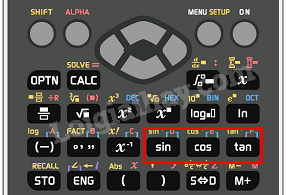
Để tính , ta tính hoặc .
Bảng tóm tắt cách tính tỉ số lượng giác của một góc nhọn
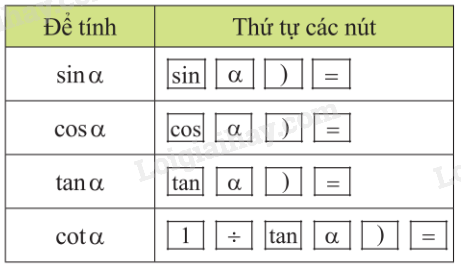
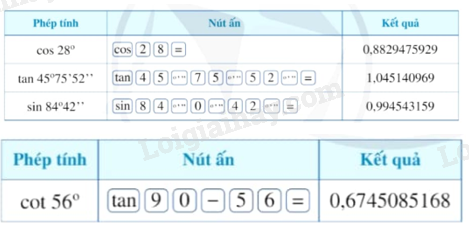
Ví dụ:
Xác định số đo của góc nhọn khi biết một tỉ số lượng giác của góc đó
Bảng tóm tắt cách tính số đo của một góc nhọn khi biết một tỉ số lượng giác

Để tìm khi biết , ta tính và dùng để tính .
Ví dụ:

Một số công thức mở rộng:
+)
+)
+)
+)
+)
+)
Sơ đồ tư duy Tỉ số lượng giác của góc nhọn
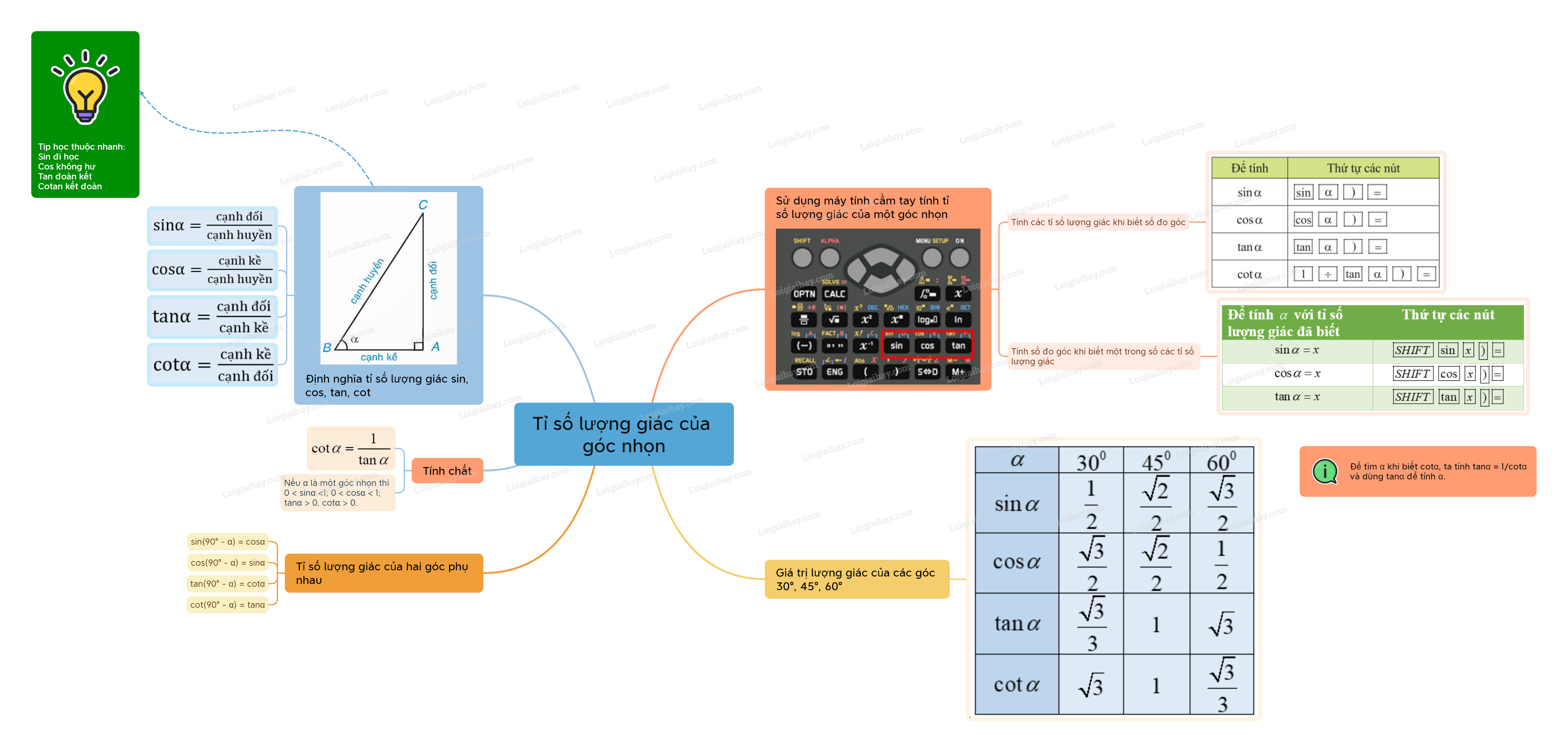
B. Bài tập Tỉ số lượng giác của góc nhọn
Bài 1. Cho tam giác ABC vuông tại A, có AB = 3; AC = 4. Tính cotC.
A. ;
B. ;
C. ;
D. .
Hướng dẫn giải
Đáp án đúng là: C
Tam giác ABC vuông tại A, có: .
Vậy ta chọn phương án C.
Bài 2. Cho α và β là hai góc nhọn bất kì thỏa mãn α + β = 90°. Khẳng định đúng là
A. tanα = sinβ;
B. tanα = cotβ;
C. tanα = cosα;
D. tanα = tanβ.
Hướng dẫn giải
Đáp án đúng là: B
Ta có α và β là hai góc nhọn bất kì thỏa mãn α + β = 90°.
Suy ra α và β là hai góc phụ nhau và β = 90° – α.
Áp dụng định lí về tỉ số lượng giác của hai góc phụ nhau, ta được:
tanα = cot(90° – α) = cotβ.
Vậy ta chọn phương án B.
Bài 3. Khi sử dụng máy tính cầm tay để tính (gần đúng) tỉ số lượng giác cos15°25’, ta nhập vào máy tính cầm tay như thế nào? (Giả sử máy tính cầm tay ở chế độ “độ”).
A.
B.
C.
D.
Hướng dẫn giải
Đáp án đúng là: A
Ta thực hiện như sau:

Bài 4. Tính giá trị các biểu thức sau mà không sử dụng máy tính bỏ túi:
a) M = sin15° + sin20° – cos70° – cos75°.
b) .
c) P = 3cos50° – 3sin40° + 2cot45°.
d) .
Hướng dẫn giải
a) M = sin15° + sin20° – cos70° – cos75°
= cos(90° – 15°) + cos(90° – 20°) – cos70° – cos75°
= cos75° + cos70° – cos70° – cos75°
= (cos75° – cos75°) + (cos70° – cos70°)
= 0.
b)
= 1.
c) P = 3cos50° – 3sin40° + 2cot45°
= 3cos50° – 3cos(90° – 40°) + 2cot45°
= 3cos50° – 3cos50° + 2cot45°
= 2cot45°
= 2.1 = 2.
d)
= 4cos60° – tan30°
Bài 5. Cho tam giác ABC vuông tại A (AB > AC), đường cao AH chia cạnh BC thành hai đoạn thẳng CH = 4 cm, BH = 9 cm. Kẻ HM ⊥ AB tại M, HN ⊥ AC tại N. Tính độ dài đoạn thẳng AH và số đo góc B, góc C của tam giác ABC (làm tròn kết quả đến phút).
Hướng dẫn giải
Xét ∆ACH và ∆BAH, có:
(cùng phụ với
Do đó ∆ACH ᔕ∆BAH (g.g).
Suy ra .
Do đó AH2 = CH.BH = 4.9 = 36.
Vì vậy AH = 6 (cm).
Tam giác AHB vuông tại H nên .
Suy ra .
Tam giác ACH vuông tại H nên .
Suy ra .
Vậy AH = 6 cm; và .
Bài 6. Một khúc sông rộng khoảng 250 m. Một con đò chèo qua sông bị dòng nước đẩy xiên nên phải chèo khoảng 320 m mới sang được bờ bên kia. Hỏi dòng nước đã đẩy con đò đi lệch một góc α bằng bao nhiêu(làm tròn đến phút)?
Hướng dẫn giải
Đặt các điểm A, B, C như hình vẽ.
Tam giác ABC vuông tại A nên .
Suy ra α ≈ 38°37’.
Vậy dòng nước đã đẩy con đò đi lệch một góc α khoảng 38°37’.
Xem thêm các bài tóm tắt Lý thuyết Toán lớp 9 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số
Lý thuyết Bài 1: Tỉ số lượng giác của góc nhọn
Lý thuyết Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông
Lý thuyết Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn
Lý thuyết Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn
Lý thuyết Bài 2: Vị trí tương đối của đường thẳng và đường tròn