Với tóm tắt lý thuyết Toán lớp 9 Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số

A. Lý thuyết Một số phép biến đổi căn thức bậc hai của biểu thức đại số

1. Căn thức bậc hai của một bình phương

Quy tắc về căn thức bậc hai của một bình phương:

Ví dụ:$\sqrt{{\left(x-2\right)}^2}=\left|x-2\right|=\{\begin{array}{l}x-2khix\ge 2\\ 2-xkhix\le 2\end{array}$

2. Căn thức bậc hai của một tích

Quy tắc về căn thức bậc hai của một tích:

Ví dụ:

$\sqrt{4a^2}=\sqrt{4}.\sqrt{a^2}=2\left|a\right|$;

$\sqrt{2a}.\sqrt{8a}=\sqrt{2a.8a}=\sqrt{16a^2}=\sqrt{16}.\sqrt{a^2}=4\left|a\right|$.

3. Căn thức bậc hai của một thương

Quy tắc về căn bậc hai của một thương

Ví dụ:

$\sqrt{\frac{4a^2}{25}}=\frac{\sqrt{4a^2}}{\sqrt{25}}=\frac{2\left|a\right|}{5}$;

$\frac{\sqrt{125a}}{\sqrt{5a}}=\sqrt{\frac{125a}{5a}}=\sqrt{25}=5$.

4. Trục căn thức ở mẫu

Nhận xét: Phép biến đổi làm mất căn thức bậc hai ở mẫu thức của một biểu thức được gọi là trục căn thức ở mẫu của biểu thức đó.

Ví dụ:

$\frac{2}{3\sqrt{5}}=\frac{2\sqrt{5}}{3{\left(\sqrt{5}\right)}^2}=\frac{2\sqrt{5}}{3.5}=\frac{2\sqrt{5}}{15}$;

$\frac{a}{3-2\sqrt{2}}=\frac{a\left(3+2\sqrt{2}\right)}{\left(3-2\sqrt{2}\right).\left(3+2\sqrt{2}\right)}=\frac{a\left(3+2\sqrt{2}\right)}{3^2-{\left(2\sqrt{2}\right)}^2}=\frac{a\left(3+2\sqrt{2}\right)}{9-8}=\left(3+2\sqrt{2}\right)a$.

Sơ đồ tư duy Một số phép biến đổi căn thức bậc hai của biểu thức đại số

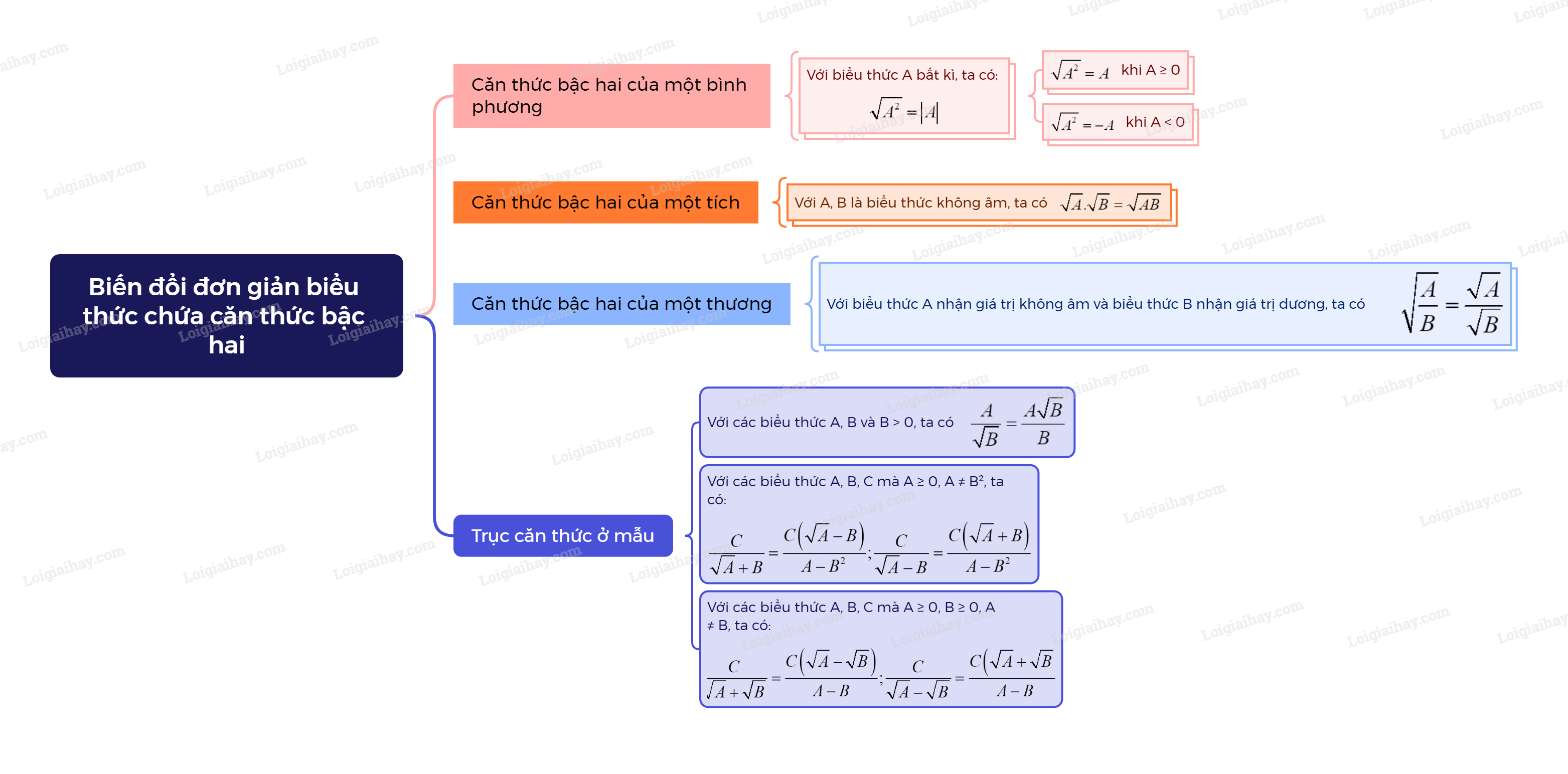
B. Bài tập Một số phép biến đổi căn thức bậc hai của biểu thức đại số

Bài 1.Cho các biểu thức A < 0 và B ≥ 0, khẳng định nào sau đây là đúng?

A. $\sqrt{A^{2}B}=A\sqrt{B};$

B. $\sqrt{A^{2}B}=-A\sqrt{B};$

C. $\sqrt{A^{2}B}=-B\sqrt{A};$

D. $\sqrt{A^{2}B}=B\sqrt{A}.$

Hướng dẫn giải

Đáp án đúng là:B

Ta có: $\sqrt{A^{2}B}=\sqrt{A^2}\cdot \sqrt{B}=-A\sqrt{B}$ (vì A < 0).

Vậy ta chọn phương án B.

Bài 2. Trục căn thức ở mẫu của biểu thức $\frac{4}{3\sqrt{x}+2\sqrt{y}}$ với x ≥ 0, y ≥ 0 và $x\ne \frac{4}{9}y$ ta được

A. $\frac{3\sqrt{x}-2\sqrt{y}}{9x-4y};$

B. $\frac{12\sqrt{x}-8\sqrt{y}}{3x+2y};$

C. $\frac{12\sqrt{x}+8\sqrt{y}}{9x+4y};$

D. $\frac{12\sqrt{x}-8\sqrt{y}}{9x-4y}.$

Hướng dẫn giải

Đáp án đúng là: D

Với x ≥ 0, y ≥ 0 và $x\ne \frac{4}{9}y$ ta có:

$\frac{4}{3\sqrt{x}+2\sqrt{y}}=\frac{4\left(3\sqrt{x}-2\sqrt{y}\right)}{\left(3\sqrt{x}+2\sqrt{y}\right)\left(3\sqrt{x}-2\sqrt{y}\right)}$

$=\frac{12\sqrt{x}-8\sqrt{y}}{{\left(3\sqrt{x}\right)}^2-{\left(2\sqrt{y}\right)}^2}=\frac{12\sqrt{x}-8\sqrt{y}}{9x-4y}.$

Bài 3.Rút gọn biểu thức $\frac{a}{\sqrt{5}+1}+\frac{a}{\sqrt{5}-2}-\frac{a}{3-\sqrt{5}}-\sqrt{5}a$ ta được:

A. 2a;

B. a;

C. 3a;

D. 12a.

Hướng dẫn giải

Đáp án đúng là: B

Ta có: $\frac{a}{\sqrt{5}+1}+\frac{a}{\sqrt{5}-2}-\frac{a}{3-\sqrt{5}}-\sqrt{5}a$

$=\frac{a\left(\sqrt{5}-1\right)}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}+\frac{a\left(\sqrt{5}+2\right)}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}-\frac{a\left(3+\sqrt{5}\right)}{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}-\sqrt{5}a$

$=\frac{a\left(\sqrt{5}-1\right)}{5-1}+\frac{a\left(\sqrt{5}+2\right)}{5-4}-\frac{a\left(3+\sqrt{5}\right)}{9-5}-\sqrt{5}a$

$=\frac{a\left(\sqrt{5}-1\right)}{4}+a\left(\sqrt{5}+2\right)-\frac{a\left(3+\sqrt{5}\right)}{4}-\sqrt{5}a$

$=\frac{a\sqrt{5}-a-3\text{a}-a\sqrt{5}}{4}+a\sqrt{5}+2\text{a}-a\sqrt{5}$

$=\frac{-4\text{a}}{4}+2\text{a=}-a+2\text{a}=a.$

Vậy ta chọn đáp án B.

Bài 4.Rút gọn các biểu thức sau:

a) $\sqrt{225\left(x^2-4x+4\right)}$ với x ≥ 2;

b) $\frac{3}{x-y}\sqrt{x^4{\left(x-y\right)}^2}$ với x < y.

Hướng dẫn giải

a) Ta có: $\sqrt{225\left(x^2-4x+4\right)}=\sqrt{{15}^2\cdot {\left(x-2\right)}^2}$

 $=\sqrt{{15}^2}\cdot \sqrt{{\left(x-2\right)}^2}=15\left|x-2\right|.$

Với x ≥ 2 thì x – 2 ≥ 0  nên |x – 2| = x – 2.

Do đó $\sqrt{225\left(x^2-4x+4\right)}=15\left|x-2\right|=15\left(x-2\right)=15x-30$

Vậy $\sqrt{225\left(x^2-4x+4\right)}=15x-30$  với x ≥ 2.

b) Cách 1:

Ta có:  $\frac{3}{x-y}\sqrt{x^4{\left(x-y\right)}^2}=\frac{3}{x-y}\sqrt{x^4}\cdot \sqrt{{\left(x-y\right)}^2}=\frac{3}{x-y}\cdot x^2\left|x-y\right|$

Với x < y thì x – y < 0 nên |x – y| = – (x – y).

Do đó $\frac{3}{x-y}\sqrt{x^4{\left(x-y\right)}^2}=\frac{3}{x-y}\cdot x^2\left|x-y\right|=\frac{3}{x-y}\cdot x^2\cdot \left[-\left(x-y\right)\right]=-3x^2.$

Vậy $\frac{3}{x-y}\sqrt{x^4{\left(x-y\right)}^2}=-3x^2$  với x < y.

Cách 2: Với x < y thì x – y < 0 nên ta có:

$\frac{3}{x-y}\sqrt{x^4{\left(x-y\right)}^2}=3\cdot \sqrt{x^4}\cdot \frac{1}{x-y}\cdot \sqrt{{\left(x-y\right)}^2}$

$=-3x^2\sqrt{\frac{1}{{\left(x-y\right)}^2}\cdot {\left(x-y\right)}^2}=-3x^2.$

Bài 5.Rút gọn biểu thức: $P=\left(\frac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\frac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}.$

Hướng dẫn giải

$P=\left(\frac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\frac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}$

$=\left[\frac{\sqrt{7}\left(\sqrt{2}-1\right)}{1-\sqrt{2}}+\frac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}\right]:\frac{1}{\sqrt{7}-\sqrt{5}}$

$=\left(-\sqrt{7}-\sqrt{5}\right)\cdot \left(\sqrt{7}-\sqrt{5}\right)$

$=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)$

= –(7 – 5) = –2.

Bài 6.Cho $A=\left(\frac{\sqrt{x}}{\sqrt{x}-2}-\frac{x-3}{x+2\sqrt{x}+4}-\frac{7\sqrt{x}+10}{x\sqrt{x}-8}\right):\left(\frac{\sqrt{x}+7}{x+2\sqrt{x}+4}\right)$ với x ≥ 0, x ≠ 4.

a) Rút gọn biểu thức A.

b) Tìm x sao cho A < 2.

Hướng dẫn giải

a)Với x ≥ 0, x ≠ 4, ta có:

$A=\left(\frac{\sqrt{x}}{\sqrt{x}-2}-\frac{x-3}{x+2\sqrt{x}+4}-\frac{7\sqrt{x}+10}{x\sqrt{x}-8}\right):\left(\frac{\sqrt{x}+7}{x+2\sqrt{x}+4}\right)$

$=\left[\frac{\sqrt{x}}{\sqrt{x}-2}-\frac{x-3}{x+2\sqrt{x}+4}-\frac{7\sqrt{x}+10}{{\left(\sqrt{x}\right)}^3-2^3}\right]\cdot \frac{x+2\sqrt{x}+4}{\sqrt{x}+7}$

$=\frac{\sqrt{x}\left(x+2\sqrt{x}+4\right)-\left(x-3\right)\left(\sqrt{x}-2\right)-7\sqrt{x}-10}{\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+4\right)}\cdot \frac{x+2\sqrt{x}+4}{\sqrt{x}+7}$

$=\frac{x\sqrt{x}+2x+4\sqrt{x}-x\sqrt{x}+2x+3\sqrt{x}-6-7\sqrt{x}-10}{\sqrt{x}-2}\cdot \frac{1}{\sqrt{x}+7}$

$=\frac{4x-16}{\sqrt{x}-2}\cdot \frac{1}{\sqrt{x}+7}=\frac{4\left(x-4\right)}{\sqrt{x}-2}\cdot \frac{1}{\sqrt{x}+7}$

$=\frac{4\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}-2}\cdot \frac{1}{\sqrt{x}+7}$

$=\frac{4\left(\sqrt{x}+2\right)}{\sqrt{x}+7}.$

Vậy với x ≥ 0, x ≠ 4 thì $A=\frac{4\left(\sqrt{x}+2\right)}{\sqrt{x}+7}.$

b)Với x ≥ 0, x ≠ 4, ta có A < 2 nên $\frac{4\left(\sqrt{x}+2\right)}{\sqrt{x}+7}<2.$

Giải bất phương trình:

$\frac{4\left(\sqrt{x}+2\right)}{\sqrt{x}+7}<2.$

$\frac{4\left(\sqrt{x}+2\right)}{\sqrt{x}+7}-2<0$

$\frac{4\left(\sqrt{x}+2\right)-2\left(\sqrt{x}+7\right)}{\sqrt{x}+7}<0$

$4\sqrt{x}+8-2\sqrt{x}-14<0$ (Do $\sqrt{x+7}>0)$

$2\sqrt{x}<6$

$\sqrt{x}<3$

x < 9.

Kết hợp điều kiện xác định ta được 0 ≤ x < 9 và x ≠ 4.

Xem thêm các bài tóm tắt Lý thuyết Toán lớp 9 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số

Lý thuyết Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số

Lý thuyết Bài 1: Tỉ số lượng giác của góc nhọn

Lý thuyết Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông

Lý thuyết Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn

Lý thuyết Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn