Với tóm tắt lý thuyết Toán lớp 9 Bài 2: Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 2: Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn

A. Lý thuyết Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn

1. Phương trình bậc nhất hai ẩn

Khái niệm phương trình bậc nhất hai ẩn

Ví dụ: $2x+3y=4$, $0x+2y=3$, $x+0y=2$ là các phương trình bậc nhất hai ẩn.

Nghiệm của phương trình bậc nhất hai ẩn

Ví dụ: Cặp số $(-1;2)$ là nghiệm của phương trình $2x+3y=4$ vì $2.\left(-1\right)+3.2=-2+6=4$.

Cặp số $(1;2)$ không là nghiệm của phương trình $2x+3y=4$ vì

$2.1+3.2=2+6=8\ne 4$.

Chú ý:

Ta cũng áp dụng được quy tắc chuyển vế, quy tắc nhân đã biết ở phương trình bậc nhất một ẩn để biến đổi phương trình bậc nhất hai ẩn.

Biểu diễn nghiệm trên mặt phẳng tọa độ Oxy

- Trong mặt phẳng tọa độ Oxy, mỗi nghiệm của phương trình $ax+by=c$ được biểu diễn bởi một điểm. Nghiệm $\left(x_0;y_0\right)$ được biểu diễn bởi điểm có tọa độ $\left(x_0;y_0\right)$.

- Mỗi nghiệm của phương trình $ax+0y=c\left(a\ne 0\right)$ được biểu diễn bởi điểm có tọa độ $\left(\frac{c}{a};y_0\right)$ $\left(y_0\in \mathbb{R}\right)$ nằm trên đường thẳng $d_1:x=\frac{c}{a}$. Đường thẳng $d_1$ là đường thẳng đi qua điểm $\frac{c}{a}$ trên trục Ox và vuông góc với trục Ox.

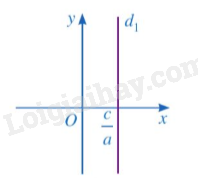
- Mỗi nghiệm của phương trình $0x+by=c\left(b\ne 0\right)$ được biểu diễn bởi một điểm có tọa độ $\left(x_0;\frac{c}{b}\right)\left(x_0\in \mathbb{R}\right)$ nằm trên đường thẳng $d_2:y=\frac{c}{b}$. Đường thẳng $d_2$ là đường thẳng đi qua điểm $\frac{c}{b}$ trên trục Oy và vuông góc với trục Oy.

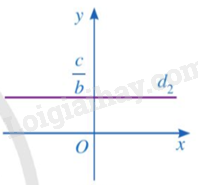
- Mỗi nghiệm của phương trình $ax+by=c\left(a\ne 0,b\ne 0\right)$ được biểu diễn bởi một điểm nằm trên đường thẳng $d_3:y=-\frac{a}{b}x+\frac{c}{b}$.

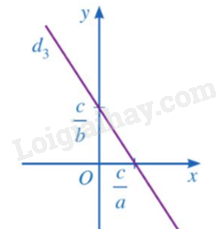
Ví dụ:

Nghiệm của phương trình $-3x+y=2$ được biểu diễn bởi đường thẳng d: $y=3x+2$.

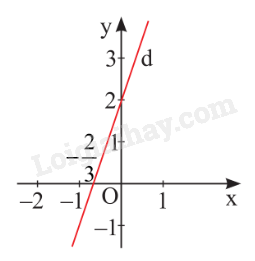
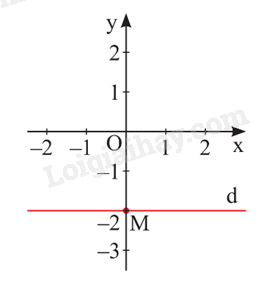
Nghiệm của phương trình $0x+y=-2$ được biểu diễn bởi đường thẳng d: $y=-2$ vuông góc với Oy tại điểm $M\left(0;-2\right)$.

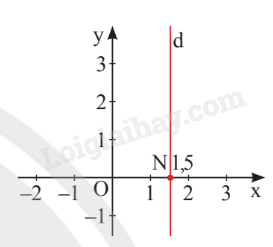
Nghiệm của phương trình $2x+0y=3$ được biểu diễn bởi đường thẳng d: $x=1,5$ vuông góc với Ox tại điểm $N\left(1,5;0\right)$.

2. Hệ hai phương trình bậc nhất hai ẩn

Khái niệm hệ hai phương trình bậc nhất hai ẩn

Ví dụ: Hệ phương trình $\{\begin{array}{l}2x-y=0\\ x+y=3\end{array}$, $\{\begin{array}{l}3x=1\\ x-y=3\end{array}$, $\{\begin{array}{l}4x-y=3\\ 3y=6\end{array}$ là các hệ phương trình bậc nhất hai ẩn.

Nghiệm của hệ hai phương trình bậc nhất hai ẩn

Ví dụ: Cặp số (1; 2) là một nghiệm của hệ phương trình $\{\begin{array}{l}2x-y=0\\ x+y=3\end{array}$, vì:

$2x-y=2.1-2=0$ nên (1; 2) là nghiệm của phương trình thứ nhất.

$x+y=1+2=3$ nên (1; 2) là nghiệm của phương trình thứ hai.

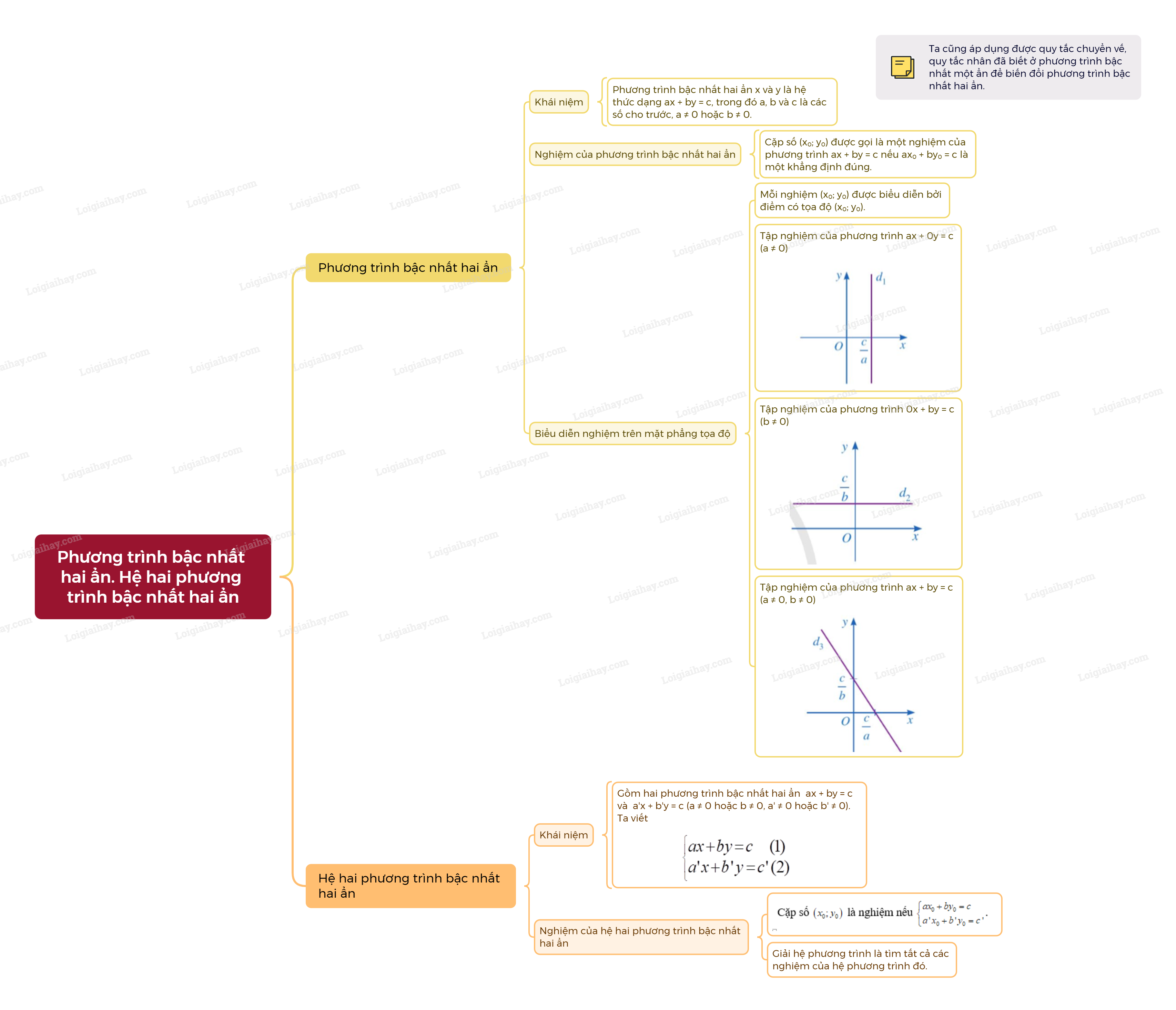
Sơ đồ tư duy Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn

B. Bài tập Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn

Bài 1. Cặp số nào sau đây là nghiệm của phương trình 5x + 4y = 8?

A. (–2; 1).

B. (0; 2).

C. (–1; 0).

D. (4; 3).

Hướng dẫn giải

Đáp án đúng là: B

Xét phương trình 5x + 4y = 8:

⦁ Thay x = –2 và y = 1, ta có: 5.(–2) + 4.1 = –2 ≠ 8.

⦁ Thay x = 0 và y = 2, ta có: 5.0 + 4.2 = 8.

⦁ Thay x = –1 và y = 0, ta có: 5.(–1) + 4.0 = –5 ≠ 8.

⦁ Thay x = 4 và y = 3, ta có: 5.4 + 4.3 = 32 ≠ 8.

Vậy (0; 2) là nghiệm của phương trình đã cho.

Bài 2. Đường thẳng d trong hình vẽ dưới đây biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn nào?

A. –2x + 0y = 0.

B. y = –2.

C. 0x + 2y = –4.

D. 2x + 0y = –4.

Hướng dẫn giải

Đáp án đúng là: D

Đường thẳng d trong hình vẽ là đường thẳng đi qua điểm –2 trên trục Ox và vuông góc với trục Ox nên đường thẳng d biểu diễn tất cả các nghiệm của phương trình x = –2.

⦁ Xét phương án A: ta có phương trình –2x + 0y = 0, hay x = 0 (loại).

⦁ Xét phương án B: ta có phương trình y = –2 (loại).

⦁ Xét phương án C: ta có phương trình 0x + 2y = –4, hay y = –2 (loại).

⦁ Xét phương án D: ta có phương trình 2x + 0y = –4, hay x = –2.

Vậy ta chọn phương án D.

Bài 3. Cặp số nào sau đây là nghiệm của hệ phương trình bậc nhất hai ẩn $\left\{\begin{array}{l}4x-5y=3\\ 3x-y=16\end{array}\right.?$

A. (–1; 3).

B. (2; 1).

C. (7; 5).

D. (5; –1).

Hướng dẫn giải

Đáp án đúng là: C

 ⦁ Thay x = –1 và y = 3 vào mỗi phương trình trong hệ, ta có:

4.(–1) – 5.3 = –19 ≠ 3;

3.(–1) – 3 = –6 ≠ 16.

Do đó cặp số (–1; 3) không là nghiệm của mỗi phương trình trong hệ.

Vậy cặp số (–1; 3) không là nghiệm của hệ phương trình đã cho.

⦁ Thay x = 2 và y = 1 vào mỗi phương trình trong hệ, ta có:

4.2 – 5.1 = 3;

3.2 – 1 = 5 ≠ 16.

Do đó cặp số (2; 1) không là nghiệm của phương trình thứ hai trong hệ.

Vậy cặp số (2; 1) không là nghiệm của hệ phương trình đã cho.

⦁ Thay x = 7 và y = 5 vào mỗi phương trình trong hệ, ta có:

4.7 – 5.5 = 3;

3.7 – 5 = 16.

Suy ra cặp số (7; 5) là nghiệm của từng phương trình trong hệ.

Vậy cặp số (7; 5) là nghiệm của hệ phương trình đã cho.

⦁ Thay x = 5 và y = –1 vào mỗi phương trình trong hệ, ta có:

4.5 – 5.(–1) = 25 ≠ 3;

3.5 – (–1) = 16.

Do đó cặp số (5; –1) không là nghiệm của phương trình thứ nhất trong hệ.

Vậy cặp số (5; –1) không là nghiệm của hệ phương trình đã cho.

Ta chọn phương án C.

Bài 4. Xét trò ném đồng xu vào trong vòng tròn như hình vẽ dưới đây:

– Lượt chơi thứ nhất (ném đồng xu 2 lần): một đồng xu rơi vào phần trong (hình tròn màu trắng), một đồng xu rơi vào phần ngoài (hình vành khăn màu đen); tổng số điểm đạt được là 17 (điểm).

– Lượt chơi thứ hai (ném đồng xu 5 lần): hai đồng xu rơi vào phần trong, ba đồng xu rơi vào phần ngoài; tổng số điểm đạt được là 41 (điểm).

Gọi x, y lần lượt là số điểm ấn định cho phần trong và phần ngoài.

a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.

b) Cặp số (10; 7) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Hướng dẫn giải

a) – Lượt chơi thứ nhất có một đồng xu rơi vào phần trong và một đồng xu rơi vào phần ngoài, đạt được 17 điểm nên ta có phương trình: x + y = 17.

– Lượt chơi thứ hai có hai đồng xu rơi vào phần trong, ba đồng xu rơi vào phần ngoài, đạt được 41 điểm nên ta có phương trình: 2x + 3y = 41.

Vậy hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng là: $\left\{\begin{array}{l}x+y=17\\ 2x+3y=41.\end{array}\right.$

b) Thay x = 10 và y = 7 vào mỗi phương trình trong hệ ở câu a, ta có:

10 + 7 = 17;

2.10 + 3.7 = 41.

Suy ra cặp số (10; 7) là nghiệm của từng phương trình trong hệ.

Vậy cặp số (10; 7) là nghiệm của hệ phương trình ở câu a.

Xem thêm các bài tóm tắt Lý thuyết Toán lớp 9 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 1: Phương trình quy về phương trình bậc nhất một ẩn

Lý thuyết Bài 2: Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn

Lý thuyết Bài 3: Giải hệ hai phương trình bậc nhất hai ẩn

Lý thuyết Bài 1: Bất đẳng thức

Lý thuyết Bài 2: Bất phương trình bậc nhất một ẩn

Lý thuyết Bài 1: Căn bậc hai và căn bậc ba của số thực