Với tóm tắt lý thuyết Toán lớp 9 Bài 1: Phương trình quy về phương trình bậc nhất một ẩn sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 1: Phương trình quy về phương trình bậc nhất một ẩn

A. Lý thuyết Phương trình quy về phương trình bậc nhất một ẩn

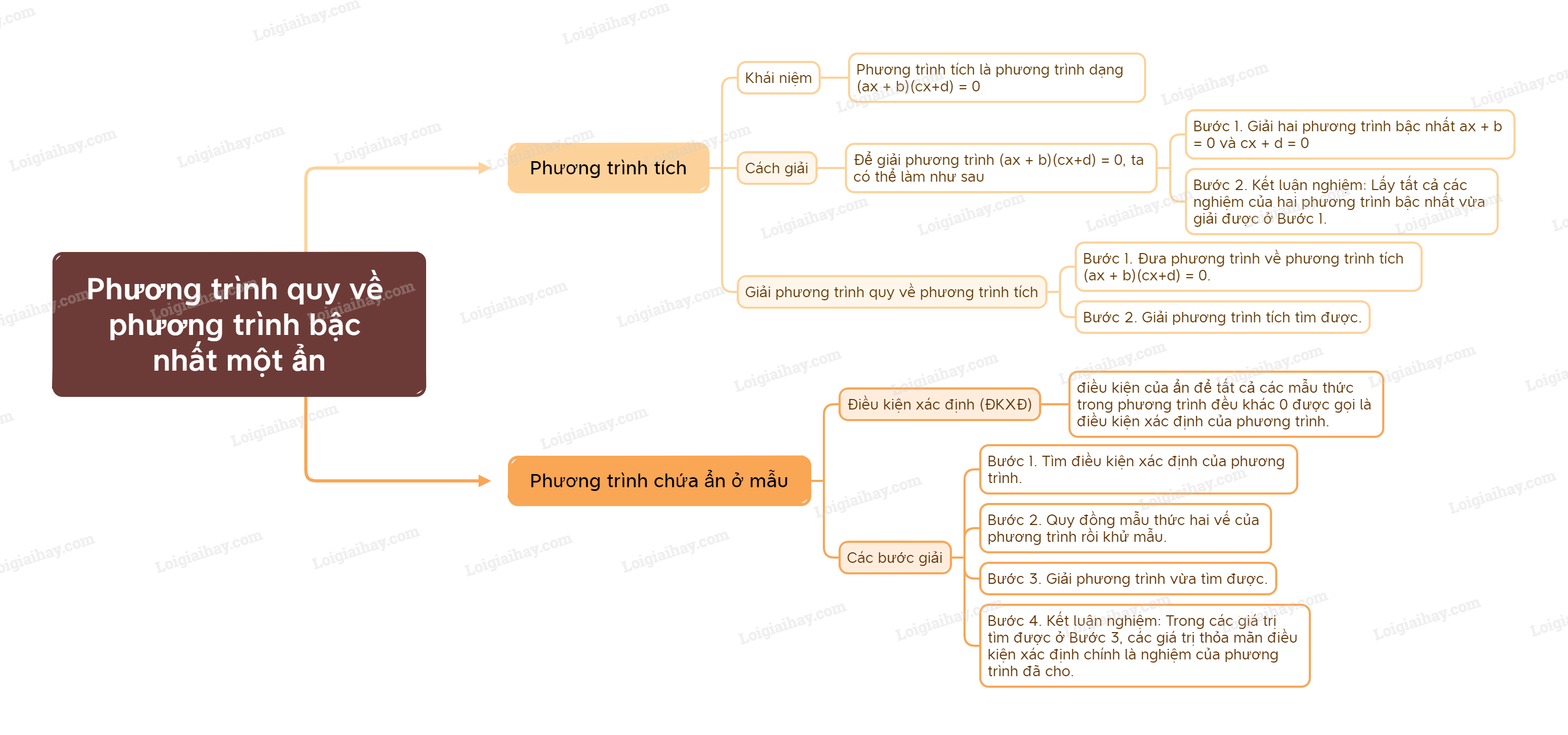
1. Phương trình tích có dạng $\left(ax+b\right)\left(cx+d\right)=0\left(a\ne 0,c\ne 0\right)$

Cách giải phương trình tích

Ví dụ 1: Giải phương trình $\left(2x+1\right)\left(3x-1\right)=0$

Lời giải:

Để giải phương trình  $\left(2x+1\right)\left(3x-1\right)=0$, ta giải hai phương trình sau:

*) $2x+1=0$

$2x=-1$

$x=-\frac{1}{2}$.

*) $3x-1=0$

$3x=1$

$x=\frac{1}{3}$.

Vậy phương trình đã cho có hai nghiệm là $x=-\frac{1}{2}$ và $x=\frac{1}{3}$.

Ví dụ 2: Giải phương trình $x^2-x=-2x+2$.

Lời giải:

Biến đổi phương trình đã cho về phương trình tích như sau:

$\begin{array}{l}{x}^2-x=-2x+2\\ x^2-x+2x-2=0\\ x\left(x-1\right)+2\left(x-1\right)=0\\ \left(x+2\right)\left(x-1\right)=0.\end{array}$

Ta giải hai phương trình sau:

*) $x+2=0$

$x=-2$.

*) $x-1=0$

$x=1$.

Vậy phương trình đã cho có hai nghiệm là $x=-2$ và $x=1$.

2. Phương trình chứa ẩn ở mẫu

Điều kiện xác định của phương trình chứa ẩn ở mẫu

Ví dụ:

- Phương trình $\frac{5x+2}{x-1}=0$ có điều kiện xác định là $x-1\ne 0$ hay $x\ne 1$.

- Phương trình $\frac{1}{x+1}=1+\frac{1}{x-2}$ có điều kiện xác định là $x+1\ne 0$ và $x-2\ne 0$ hay $x\ne -1$ và $x\ne 2$.

Các bước giải phương trình chứa ẩn ở mẫu

Ví dụ: Giải phương trình $\frac{2}{x+1}+\frac{1}{x-2}=\frac{3}{\left(x+1\right)\left(x-2\right)}$

Lời giải:

Điều kiện xác định $x\ne -1$ và $x\ne 2$.

$\frac{2}{x+1}+\frac{1}{x-2}=\frac{3}{\left(x+1\right)\left(x-2\right)}$

$\frac{2\left(x-2\right)+\left(x+1\right)}{\left(x+1\right)\left(x-2\right)}=\frac{3}{\left(x+1\right)\left(x-2\right)}$

$2\left(x-2\right)+\left(x+1\right)=3$.

$\begin{array}{l}2\left(x-2\right)+\left(x+1\right)=3\\ 2x-4+x+1=3\\ 3x-3=3\\ 3x=6\\ x=2\end{array}$

Ta thấy $x=2$ không thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình $\frac{2}{x+1}+\frac{1}{x-2}=\frac{3}{\left(x+1\right)\left(x-2\right)}$ vô nghiệm.

Sơ đồ tư duy Phương trình quy về phương trình bậc nhất một ẩn

B. Bài tập Phương trình quy về phương trình bậc nhất một ẩn

Bài 1. Một người đi xe đạp từ A đến B cách nhau 24 km. Khi từ B trở về A (cùng cung đường khi đi từ A đến B), người đó tăng vận tốc thêm 4 km/h so với lúc đi nên lúc về mất ít thời gian hơn so với lúc đi là 30 phút. Tính vận tốc của người xe đạp khi đi từ A đến B.

Hướng dẫn giải

Đổi 30 phút $=\frac{1}{2}$ giờ.

Gọi vận tốc của người đi xe đạp khi đi từ A đến B là x (km/h, x > 0).

Thời gian người đó đi từ A đến B là $\frac{24}{x}$ (giờ).

Khi từ B trở về A, người đó tăng vận tốc thêm 4 km/h so với lúc đi nên lúc trở về, vận tốc của người đó là: x + 4 (km/h).

Thời gian người đó từ B trở về A là: $\frac{24}{x+4}$ (giờ).

Theo bài, lúc về mất ít thời gian hơn so với lúc đi là 30 phút nên ta có phương trình: $\frac{24}{x}-\frac{24}{x+4}=\frac{1}{2}.$

Giải phương trình:

$\frac{24}{x}-\frac{24}{x+4}=\frac{1}{2}$

$\frac{24\cdot 2\left(x+4\right)}{2x\left(x+4\right)}-\frac{24\cdot 2x}{2x\left(x+4\right)}=\frac{x\left(x+4\right)}{2x\left(x+4\right)}$

24.2(x + 4) – 24.2x = x(x + 4)

48x + 192 – 48x = x² + 4x

192 = x² + 4x

x²– 12x + 16x – 192 = 0

x(x – 12) + 16(x – 12) = 0

(x – 12)(x + 16) = 0

x – 12 = 0 hoặc x + 16 = 0

x = 12 hoặc x = –16.

Ta thấy chỉ có x = 12 thỏa mãn điều kiện x > 0.

Vậy vận tốc người xe đạp khi đi từ A đến B là 12 km/h.

Bài 2. Hai bến sông A và B cách nhau 40 km. Cùng một lúc với ca nô xuôi từ bến A có một chiếc bè trôi từ bến A với vận tốc 3 km/h. Sau khi đến bến B, ca nô ngược dòng quay trở về bến A ngay và gặp bè, khi đó bè đã trôi được 8 km. Tính vận tốc riêng của ca nô.

Hướng dẫn giải

Gọi vận tốc riêng ca nô là x (km/h), x > 3.

Vận tốc của bè trôi xuôi dòng từ A đến B chính là vận tốc của dòng nước, nên vận tốc ca nô xuôi dòng là x + 3 (km/h).

Thời gian ca nô xuôi dòng từ A đến B là $\frac{40}{x+3}$ (giờ).

Vận tốc ca nô ngược dòng là x – 3 (km/h).

Quãng đường ca nô ngược dòng từ B đến địa điểm gặp bè là: 40 – 8 = 32 (km).

Thời gian ca nô ngược dòng từ B đến địa điểm gặp bè là: $\frac{32}{x-3}$ (giờ).

Thời gian bè trôi là: $\frac{8}{3}$ (giờ).

Theo bài, ta có phương trình:

$\frac{40}{x+3}+\frac{32}{x-3}=\frac{8}{3}$

$\frac{5}{x+3}+\frac{4}{x-3}=\frac{1}{3}$

$\frac{5\cdot 3\left(x-3\right)}{3\left(x+3\right)\left(x-3\right)}+\frac{4\cdot 3\left(x+3\right)}{3\left(x+3\right)\left(x-3\right)}=\frac{1\cdot \left(x+3\right)\left(x-3\right)}{3\left(x+3\right)\left(x-3\right)}$

5.3(x – 3) + 4.3(x + 3) = (x + 3)(x – 3)

15x – 45 + 12x + 36 = x² – 9

27x – 9 = x² – 9

x² – 27x = 0

x(x – 27) = 0

x = 0 hoặc x – 27 = 0

x = 0 hoặc x = 27.

Ta thấy chỉ x = 27 thỏa mãn điều kiện x > 3.

Vậy vận tốc riêng của cano là: 27 km/h.

Bài 3. Tất cả các nghiệm của phương trình (x + 3)(2x – 6) = 0 là

A. x = –3.

B. x = 3.

C. x = 3 và x = –3.

D. x = 2.

Hướng dẫn giải

Đáp án đúng là: C

Để giải phương trình (x + 3)(2x – 6) = 0, ta giải hai phương trình sau:

⦁ x + 3 = 0

         x = –3.

⦁ 2x – 6 = 0

         2x = 6

           x = 3.

Vậy phương trình đã cho có hai nghiệm là x = 3 và x = –3.

Bài 4. Điều kiện xác định của phương trình $\frac{x}{2x-1}+\frac{3}{x+5}=\frac{x}{\left(2x-1\right)\left(x+5\right)}$ là

A. x ≠ $\frac{1}{2}.$

B. x ≠ $\frac{1}{2}$ và x ≠ –5.

C. x ≠ 0.

D. x ≠ –5.

Hướng dẫn giải

Đáp án đúng là: B

Điều kiện xác định của phương trình đã cho là 2x – 1 ≠ 0 và x + 5 ≠ 0 hay x ≠ $\frac{1}{2}$ và x ≠ –5.

Bài 5. Giải các phương trình sau:

a) x(22x – 12) = 0;

b) (4x – 1)² – 9x² = 0.

Hướng dẫn giải

a) (x + 21)(22x – 12) = 0

Để giải phương trình đã cho, ta giải hai phương trình sau:

⦁ x + 21 = 0

           x = –21;

⦁ 22x – 12 = 0

            22x = 12

                 $x=\frac{12}{22}$

                $x=\frac{6}{11}.$

Vậy phương trình đã cho có hai nghiệm là x = –21 và $x=\frac{6}{11}.$

b) (4x – 1)² – 9x² = 0

(4x – 1)² – (3x)² = 0

(4x – 1 – 3x)(4x – 1 + 3x) = 0

(x – 1)(7x – 1) = 0.

Để giải phương trình trên, ta giải hai phương trình sau:

⦁ x – 1 = 0

        x = 1;

⦁ 7x – 1 = 0

         7x = 1

          $x=\frac{1}{7}.$

Vậy phương trình đã cho có hai nghiệm là x = 1 và $x=\frac{1}{7}.$

Bài 6. Giải các phương trình sau:

a) $\frac{x}{2x-5}=\frac{4}{3};$

b) $\frac{x+1}{x-1}-\frac{x-1}{x+1}=\frac{4}{\left(x-1\right)\left(x+1\right)}.$

Hướng dẫn giải

a) Điều kiện xác định: $x\ne \frac{5}{2}.$

$\frac{x}{2x-5}=\frac{4}{3}$

$\frac{3x}{3\left(2x-5\right)}=\frac{4\left(2x-5\right)}{3\left(2x-5\right)}$

3x = 4(2x – 5)

3x = 8x – 20

–5x = –20

    x = 4.

Ta thấy x = 4 thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho có nghiệm x = 4.

b) Điều kiện xác định: x ≠ 1 và x ≠ –1.

$\frac{x+1}{x-1}-\frac{x-1}{x+1}=\frac{4}{\left(x-1\right)\left(x+1\right)}$

$\frac{{\left(x+1\right)}^2}{\left(x-1\right)\left(x+1\right)}-\frac{{\left(x-1\right)}^2}{\left(x-1\right)\left(x+1\right)}=\frac{4}{\left(x-1\right)\left(x+1\right)}$

(x + 1)² – (x – 1)² = 4

x² + 2x + 1 – (x² – 2x + 1) = 4

x² + 2x + 1 – x² + 2x – 1 = 4

4x = 4

  x = 1.

Ta thấy x = 1 không thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho vô nghiệm.

Xem thêm các bài tóm tắt Lý thuyết Toán lớp 9 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 1: Phương trình quy về phương trình bậc nhất một ẩn

Lý thuyết Bài 2: Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn

Lý thuyết Bài 3: Giải hệ hai phương trình bậc nhất hai ẩn

Lý thuyết Bài 1: Bất đẳng thức

Lý thuyết Bài 2: Bất phương trình bậc nhất một ẩn

Lý thuyết Bài 1: Căn bậc hai và căn bậc ba của số thực