Với tóm tắt lý thuyết Toán lớp 9 Bài 1: Phương trình quy về phương trình bậc nhất một ẩn sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 1: Phương trình quy về phương trình bậc nhất một ẩn

A. Lý thuyết Phương trình quy về phương trình bậc nhất một ẩn

1. Phương trình tích

Phương trình tích là phương trình có dạng $\left(ax+b\right)\left(cx+d\right)=0$.

Cách giải phương trình tích

Ví dụ: Giải phương trình $\left(2x+1\right)\left(3x-1\right)=0$

Lời giải:

Ta có: $\left(2x+1\right)\left(3x-1\right)=0$

$2x+1=0$ hoặc $3x-1=0$.

$2x=-1$ hoặc $3x=1$

$x=-\frac{1}{2}$ hoặc $x=\frac{1}{3}$

Vậy phương trình đã cho có hai nghiệm là $x=-\frac{1}{2}$ và $x=\frac{1}{3}$.

Các bước giải phương trình:

Ví dụ: Giải phương trình $x^2-x=-2x+2$.

Lời giải:

Biến đổi phương trình đã cho về phương trình tích như sau:

$\begin{array}{l}{x}^2-x=-2x+2\\ x^2-x+2x-2=0\\ x\left(x-1\right)+2\left(x-1\right)=0\\ \left(x+2\right)\left(x-1\right)=0.\end{array}$

$x+2=0$ hoặc $x-1=0$.

$x=-2$ hoặc $x=1$.

Vậy phương trình đã cho có hai nghiệm là $x=-2$ và $x=1$.

2. Phương trình chứa ẩn ở mẫu quy về phương trình bậc nhất

Điều kiện xác định của phương trình chứa ẩn ở mẫu

Ví dụ:

- Phương trình $\frac{5x+2}{x-1}=0$ có điều kiện xác định là $x\ne 1$ vì $x-1\ne 0$ khi $x\ne 1$.

- Phương trình $\frac{1}{x+1}=1+\frac{1}{x-2}$ có điều kiện xác định là $x\ne -1$ và $x\ne 2$ vì $x+1\ne 0$ khi $x\ne -1$, $x-2\ne 0$ khi $x\ne 2$.

Các bước giải phương trình chứa ẩn ở mẫu

Ví dụ: Giải phương trình $\frac{2}{x+1}+\frac{1}{x-2}=\frac{3}{\left(x+1\right)\left(x-2\right)}$

Lời giải:

Điều kiện xác định $x\ne -1$ và $x\ne 2$.

Ta có: $\frac{2}{x+1}+\frac{1}{x-2}=\frac{3}{\left(x+1\right)\left(x-2\right)}$

$\frac{2\left(x-2\right)+\left(x+1\right)}{\left(x+1\right)\left(x-2\right)}=\frac{3}{\left(x+1\right)\left(x-2\right)}$

$2\left(x-2\right)+\left(x+1\right)=3$

$\begin{array}{l}2\left(x-2\right)+\left(x+1\right)=3\\ 2x-4+x+1=3\\ 3x-3=3\\ 3x=6\\ x=2\end{array}$

Giá trị $x=2$ không thỏa mãn ĐKXĐ.

Vậy phương trình $\frac{2}{x+1}+\frac{1}{x-2}=\frac{3}{\left(x+1\right)\left(x-2\right)}$ vô nghiệm.

Sơ đồ tư duy Phương trình quy về phương trình bậc nhất một ẩn

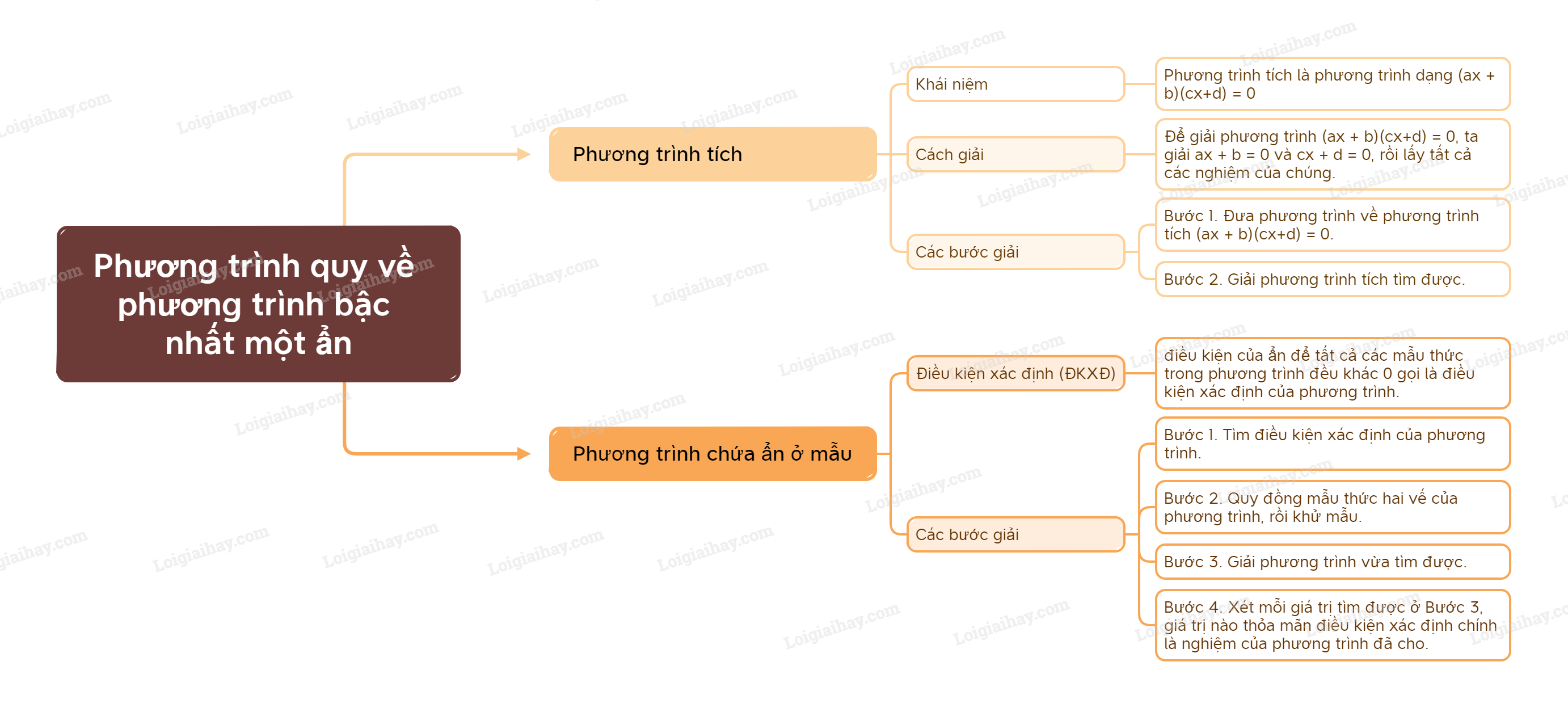
B. Bài tập Phương trình quy về phương trình bậc nhất một ẩn

Bài 1. Giải các phương trình:

a) 4x(x + 2) = 0;

b) (2x – 8)(x – 7) = 0;

c) 3x – x² = 0;

d) (x – 4)² – 25x² = 0.

Hướng dẫn giải

a) Ta có 4x(x + 2) = 0

4x = 0 hoặc x + 2 = 0

x = 0 hoặc x = –2.

Vậy phương trình đã cho có hai nghiệm là x = 0 và x = –2.

b) Ta có (2x – 8)(x – 7) = 0

2x – 8 = 0 hoặc x – 7 = 0

2x = 8 hoặc x = 7

x = 4 hoặc x = 7.

Vậy phương trình đã cho có hai nghiệm là x = 4 và x = 7.

c) Ta có 3x – x² = 0

x(3 – x) = 0

x = 0 hoặc 3 – x = 0

x = 0 hoặc x = 3.

Vậy phương trình đã cho có hai nghiệm là x = 0 và x = 3.

d) Ta có (x – 3)² – 16x² = 0

(x – 3)² – (4x)² = 0

(x – 3 + 4x)(x – 3 – 4x) = 0

(5x – 3)(–3x – 3) = 0

5x – 3 = 0 hoặc –3x – 3 = 0

5x = 3 hoặc 3x = –3

$x=\frac{3}{5}$hoặc x = –1.

Vậy phương trình đã cho có hai nghiệm là $x=\frac{3}{5}$và x = –1.

Bài 2. Tìm điều kiện xác định của mỗi phương trình sau:

a) $\frac{x+2}{4x-1}=1;$

b) $1-\frac{2}{x-3}=\frac{x+1}{2x-1}.$

Hướng dẫn giải

a) Điều kiện xác định của phương trình là 4x – 1 ≠ 0 hay $x\ne \frac{1}{4}.$

b) Ta có x – 3 ≠ 0 khi x ≠ 3 và 2x – 1 ≠ 0 khi $x\ne \frac{1}{2}.$

Vậy điều kiện xác định của phương trình là x ≠ 3 và $x\ne \frac{1}{2}.$

Bài 3. Giải các phương trình:

a) $\frac{2x}{x+2}-2=\frac{x}{x+2};$

b) $\frac{x-1}{x-3}-\frac{1}{x+3}=\frac{3x+3}{\left(x-3\right)\left(x+3\right)};$

c) $\frac{x-1}{x+2}-\frac{x}{x-2}=\frac{4-6x}{x^2-4}.$

Hướng dẫn giải

a) Điều kiện xác định: x + 2 ≠ 0 hay x ≠-2.

Ta có $\frac{2x}{x+2}-2=\frac{x}{x+2}$

$\frac{2x-2\left(x+2\right)}{x+2}=\frac{x}{x+2}$

2x – 2(x + 2) = x

2x – 2x – 4 = x

x = -4 (thỏa mãn điều kiện)

Vậy phương trình đã cho có hai nghiệm là x = –4.

b) Điều kiện xác định: x ≠ 3 và x ≠ –3.

Ta có $\frac{x-1}{x-3}-\frac{1}{x+3}=\frac{3x+3}{\left(x-3\right)\left(x+3\right)}$

$\frac{\left(x-1\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}-\frac{x-3}{\left(x-3\right)\left(x+3\right)}=\frac{3x+3}{\left(x-3\right)\left(x+3\right)}$

(x – 1)(x + 3) – (x – 3) = 3x + 3

x² + 2x – 3 – x + 3 = 3x + 3

x² + x = 3x + 3

x(x + 1) = 3(x + 1)

x(x + 1) -3(x + 1) = 0

(x + 1)(x -3) = 0

x + 1 = 0 hoặc x -3 = 0

x =-1 (thỏa mãn điều kiện) hoặc x = 3 (không thỏa mãn điều kiện).

Vậy phương trình đã cho có hai nghiệm là x = -1.

c) Điều kiện xác định: x ≠ 2 và x ≠ –2.

Ta có $\frac{x-1}{x+2}-\frac{x}{x-2}=\frac{4-6x}{x^2-4}$

$\frac{x-1}{x+2}-\frac{x}{x-2}=\frac{4-6x}{\left(x-2\right)\left(x+2\right)}$

$\frac{\left(x-1\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}-\frac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\frac{4-6x}{\left(x-2\right)\left(x+2\right)}$

$\frac{x^2-x-2x+2}{\left(x-2\right)\left(x+2\right)}-\frac{x^2+2x}{\left(x-2\right)\left(x+2\right)}=\frac{4-6x}{\left(x-2\right)\left(x+2\right)}$

$\frac{-5x+2}{\left(x-2\right)\left(x+2\right)}=\frac{4-6x}{\left(x-2\right)\left(x+2\right)}$

-5x + 2 = 4 - 6x

6x - 5x = 4 - 2

x = 2 (không thỏa mãn điều kiện xác định).

Vậy phương trình đã cho vô nghiệm.

Xem thêm các bài tóm tắt Lý thuyết Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 1: Phương trình quy về phương trình bậc nhất một ẩn

Lý thuyết Bài 2: Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn

Lý thuyết Bài 3: Giải hệ hai phương trình bậc nhất hai ẩn

Lý thuyết Bài 1: Bất đẳng thức

Lý thuyết Bài 2: Bất phương trình bậc nhất một ẩn

Lý thuyết Bài 1: Căn bậc hai