Với tóm tắt lý thuyết Toán lớp 9 Bài 3: Giải hệ hai phương trình bậc nhất hai ẩn sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 3: Giải hệ hai phương trình bậc nhất hai ẩn

A. Lý thuyết Giải hệ hai phương trình bậc nhất hai ẩn

1. Cách giải hệ phương trình bằng phương pháp thế

Ví dụ:

1. Hệ phương trình $\{\begin{array}{l}2x-y=3\\ x+2y=4\end{array}$ được giải bằng phương pháp thế như sau:

Từ phương trình thứ nhất của hệ, ta có $y=2x-3$.

Thế vào phương trình thứ hai của hệ, ta được $x+2\left(2x-3\right)=4$ hay $5x-6=4$, suy ra $x=2$.

Từ đó $y=2.2-3=1$.

Vậy hệ phương trình đã cho có nghiệm là $\left(2;1\right)$.

2. Hệ phương trình $\{\begin{array}{l}x-y=-2\\ 2x-2y=8\end{array}$ được giải bằng phương pháp thế như sau:

Từ phương trình thứ nhất của hệ, ta có $x=y-2$.

Thế vào phương trình thứ hai của hệ, ta được $2\left(y-2\right)-2y=8$ hay $0y-4=8$.

Do không có giá trị vào của y thỏa mãn hệ thức $0y-4=8$ nên hệ phương trình vô nghiệm.

3. Hệ phương trình $\{\begin{array}{l}-x+y=-2\\ 3x-3y=6\end{array}$ được giải bằng phương pháp thế như sau:

Từ phương trình thứ nhất của hệ, ta có $y=x-2$.

Thế vào phương trình thứ hai của hệ, ta được $3x-3\left(x-2\right)=6$ hay $0x=0$.

Ta thấy mọi giá trị của x đều thỏa mãn $0x=0$.

Với giá trị tùy ý của x, giá trị tương ứng của y được tính bởi $y=x-2$.

Vậy hệ phương trình có nghiệm là $\left(x;x-2\right)$ với $x\in \mathbb{R}$ tùy ý.

2. Cách giải hệ phương trình bằng phương pháp cộng đại số:

Ví dụ:

1. Hệ phương trình $\{\begin{array}{l}5x-7y=9\\ 5x-3y=1\end{array}$ được giải bằng phương pháp cộng đại số như sau:

Trừ từng vế hai phương trình ta được $\left(5x-5x\right)+\left(-7y+3y\right)=9-1$ hay $-4y=8$, suy ra $y=-2$.

Thế $y=-2$ vào phương trình thứ hai ta được $5x-7.\left(-2\right)=9$ hay $5x+14=9$, suy ra $x=-1$.

Vậy hệ phương trình đã cho có nghiệm duy nhất là (-1;-2).

2. Hệ phương trình $\{\begin{array}{l}3x-5y=2\\ -6x+10y=-4\end{array}$ được giải bằng phương pháp cộng đại số như sau:

Chia hai vế của phương trình thứ hai cho 2, ta được hệ $\{\begin{array}{l}3x-5y=2\\ -3x+5y=-2\end{array}$

Cộng từng vế hai phương trình của hệ mới ta có $0x+0y=0$. Hệ này luôn thỏa mãn với các giá trị tùy ý của x và y.

Với giá trị tùy ý của x, giá trị của y được tính nhờ hệ thức $3x-5y=2$, suy ra $y=\frac{3}{5}x-\frac{2}{5}$.

Vậy hệ phương trình đã cho cho nghiệm là $\left(x;\frac{3}{5}x-\frac{2}{5}\right)$ với $x\in \mathbb{R}$.

3. Cách tìm nghiệm của hệ hai phương trình bằng máy tính cầm tay

Ví dụ: Giải hệ $\{\begin{array}{l}2x+y-4=0\\ -2x+y=0\end{array}$, ta viết nó dưới dạng $\{\begin{array}{l}2x+y=4\\ -2x+y=0\end{array}$.

Khi đó, ta có $a_1=2$, $b_1=1$, $c_1=4$, $a_2=-2$, $b_2=1$, $c_2=0$. Lần lượt thực hiện các bước sau:

Bước 1. Vào chức năng hệ hai phương trình bậc nhất hai ẩn bằng cách nhấn MENU rồi bấm phím 9 để chọn tính năng Equation/Func (Ptrình/HệPtrình).

Bấm phím 1 để chọn Simul Equation (hệ phương trình).

Cuối cùng, bấm phím 2 để giải hệ hai phương trình bậc nhất

Bước 2. Ta nhập các hệ số $a_1,b_1,c_1,a_2,b_2,c_2$ bằng cách bấm

Bước 3. Sau khi nhập xong, ta bấm phím =, màn hình hiện x = 1; tiếp tục bấm =, màn hình hiện y = 3. Ta hiểu nghiệm của hệ phương trình là (-1;2).

Chú ý:

- Muốn xóa số vừa mới nhập thì bấm phím AC, muốn thay đổi số đã nhập ở vị trí nào đó thì di chuyển con trỏ đến vị trí đó rồi nhập số mới.

- Bấm phím ▲ hay ▼ để chuyển hiển thị các giá trị của x và y trong kết quả.

- Nếu máy báo Infinite Solution thì hệ phương trình đã cho có vô số nghiệm.

Nếu máy báo No Solution thì hệ phương trình đã cho vô nghiệm.

4. Giải bài toán bằng cách lập hệ phương trình

Các bước giải bài toán bằng cách lập hệ phương trình:

Ví dụ 1: Giải bài toán bằng cách lập hệ phương trình

Hai xe cùng khởi hành một lúc ở hai tỉnh A và tỉnh B cách nhau 60km. Nếu đi ngược chiều thì gặp nhau sau 1 giờ; nếu đi cùng chiều thì xe đi nhanh sẽ đuổi kịp xe kia sau 3 giờ. Tìm vận tốc mỗi xe.

Lời giải:

Gọi x là vận tốc của xe đi nhanh, y là vận tốc của xe đi chậm ( $x,y>0;x>y$ và x, y tính bằng km/h).

Sau 1 giờ hai xe gặp nhau, nên ta có phương trình:

x + y = 60

Sau 3 giờ mỗi xe đi được 3x; 3y ( km) và gặp nhau, nên ta có phương trình:

3x – 3y = 60.

Vậy, ta có hệ phương trình:

$\begin{array}{l}\{\begin{array}{l}x+y=60\\ 3x-3y=60\end{array}\\ \{\begin{array}{l}3x+3y=180\\ 3x-3y=60\end{array}\end{array}$

$\{\begin{array}{l}x=40\\ y=20\end{array}$

($x=40;y=20$ thỏa mãn các điều kiện đã nêu)

Vậy xe đi nhanh có vận tốc $40(km/h)$, xe đi chậm có vận tốc $20(km/h)$.

Ví dụ 2: Giải bài toán bằng cách lập hệ phương trình

Tìm một số có hai chữ số, biết rằng tổng của hai chữ số ấy bằng 12 và khi thay đổi thứ tự hai chữ số thì được một số lớn hơn số cũ là 18.

Lời giải:

Gọi x, y là các chữ số hàng chục và hàng đơn vị của số đã cho ($x\in \mathbb{N}$,$0<x\le 9$ ,$0\le x\le 9$)

Khi đó hai số có dạng $\overline{xy}=10x+y$ và $\overline{yx}=10y+x.$

Ta có hệ phương trình:

$\{\begin{array}{l}x+y=12\\ 10y+x-18=10x+y\end{array}$

$\{\begin{array}{l}x+y=12\\ x-y=2\end{array}$

$\{\begin{array}{l}x=5\\ y=7\end{array}$

Vậy số cần tìm là 57.

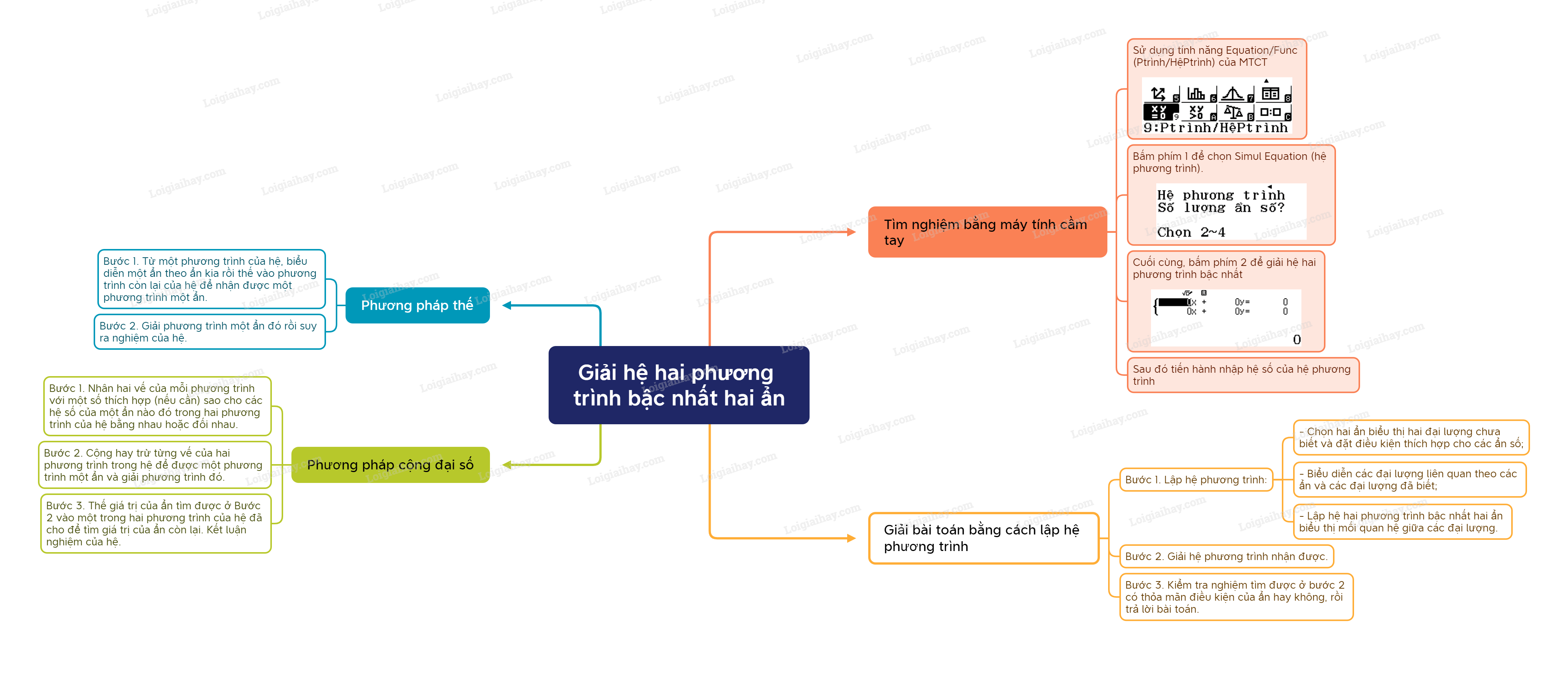
Sơ đồ tư duy Giải hệ hai phương trình bậc nhất hai ẩn

B. Bài tập Giải hệ hai phương trình bậc nhất hai ẩn

Bài 1. Giải các hệ phương trình:

a) $\left\{\begin{array}{l}x+2y=5\\ 2x-5y=1;\end{array}\right.$

b) $\left\{\begin{array}{l}5x+6y=6\\ 5x+2y=2;\end{array}\right.$

c) $\left\{\begin{array}{l}5x-4y=3\\ 2x+y=4.\end{array}\right.$

Hướng dẫn giải

a) $\left\{\begin{array}{l}x+2y=5\\ 2x-5y=1\end{array}\right.$

$\left\{\begin{array}{l}x=5-2y\\ 2(5-2y)-5y=1\end{array}\right.$

$\left\{\begin{array}{l}x=5-2y\\ -9y=-9\end{array}\right.$

$\left\{\begin{array}{l}x=3\\ y=1\end{array}\right.$

Vậy hệ phương trình có nghiệm duy nhất là (3; 1).

b) $\left\{\begin{array}{l}5x+6y=6\\ 5x+2y=2\end{array}\right.$

$\left\{\begin{array}{l}5x+6y-(5x+2y)=6-2\\ x=\frac{2-2y}{5}\end{array}\right.$

$\left\{\begin{array}{l}4y=4\\ x=\frac{2-2y}{5}\end{array}\right.$

$\left\{\begin{array}{l}y=1\\ x=0\end{array}\right.$

Vậy hệ phương trình có nghiệm duy nhất là (0; 1).

c) $\left\{\begin{array}{l}5x-4y=3\\ 2x+y=4\end{array}\right.$

$\left\{\begin{array}{l}5x-4\left(4-2x\right)=3\\ y=4-2x\end{array}\right.$

$\left\{\begin{array}{l}5x-16+8x=3\\ y=4-2x\end{array}\right.$

$\left\{\begin{array}{l}13x=19\\ y=4-2x\end{array}\right.$

$\left\{\begin{array}{l}x=\frac{19}{13}\\ y=\frac{14}{13}\end{array}\right.$

Vậy hệ phương trình có nghiệm duy nhất là $\left(\frac{19}{13};\frac{14}{13}\right)$

Bài 2. Giải các hệ phương trình:

a) $\left\{\begin{array}{l}8x-4y=-12\\ -8x+9y=3;\end{array}\right.$

b) $\left\{\begin{array}{l}12x+18y=-24\\ -2x-3y=4;\end{array}\right.$

c) $\left\{\begin{array}{l}\left(x+1\right)\left(y-1\right)=xy-1\\ \left(x-3\right)(y-3)=xy-3.\end{array}\right.$

Hướng dẫn giải

a) Cộng từng vế hai phương trình của hệ mới, ta được 5y = –9 hay $y=-\frac{9}{5}.$

Thế $y=-\frac{9}{5}$vào phương trình thứ nhất của hệ đã cho, ta có $2x+\frac{9}{5}=–3$hay $2x=-\frac{24}{5},$ suy ra $x=-\frac{12}{5}.$

Vậy hệ phương trình đã cho có nghiệm là $\left(-\frac{12}{5};-\frac{9}{5}\right).$

b) Nhân hai vế của phương trình thứ hai với 6, ta được hệ phương trình sau:

$\left\{\begin{array}{l}12x+18y=-24\\ -12x-18y=24.\end{array}\right.$

Cộng từng vế hai phương trình của hệ trên, ta được phương trình:

0x + 0y = 0, hay 0x = 0. Phương trình này có vô số nghiệm x ∈ ℝ.

Từ phương trình thứ hai ta có 3y = –2x – 4, suy ra $y=-\frac{2}{3}x-\frac{4}{3}.$

Vậy hệ phương trình đã cho có vô số nghiệm$\left\{\begin{array}{l}x\in ℝ\\ y=-\frac{2}{3}x-\frac{4}{3}.\end{array}\right.$

c) $\left\{\begin{array}{l}\left(x+1\right)\left(y-1\right)=xy-1\\ \left(x-3\right)(y-3)=xy-3\end{array}\right.$

$\left\{\begin{array}{l}xy-x+y-1=xy-1\\ xy-3x-3y+9=xy-3\end{array}\right.$

$\left\{\begin{array}{l}-x+y=0\\ -3x-3y=-12\end{array}\right.$

$\left\{\begin{array}{l}x-y=0\\ x+y=4\end{array}\right.$

$\left\{\begin{array}{l}x=y\\ x+x=4\end{array}\right.$

$\left\{\begin{array}{l}x=y\\ 2x=4\end{array}\right.$

$\left\{\begin{array}{l}x=2\\ y=2\end{array}\right.$

Vậy hệ phương trình có nghiệm duy nhất là (2; 2).

Bài 3. Xác định a, b để đồ thị hàm số y = ax + b đi qua hai điểm A(2; 1) và B(4; –2).

Hướng dẫn giải

• Đồ thị hàm số y = ax + b đi qua hai điểm A(2; 1) nên

1 = a . 2 + b hay 2a + b = 1.(1)

• Đồ thị hàm số y = ax + b đi qua hai điểm B(4; –2) nên

–2 = a . 4 + b hay 4a + b = –2.(2)

Từ (1) và (2) ta có hệ phương trình $\left\{\begin{array}{l}2a+b=1\\ 4a+b=-2\end{array}\right.$(I)

Trừ từng vế hai phương trình của hệ (I), ta được –2a = 3. Suy ra $a=-\frac{3}{2}$

Thay $a=-\frac{3}{2}$ vào phương trình thứ nhất của hệ (I), ta được

$2\cdot \left(-\frac{3}{2}\right)+b=1$hay –3 + b = 1 nên b = 4.

Vậy $a=-\frac{3}{2}$; b = 4.

Bài 4. Hai vòi nước cùng chảy vào một bể cạn trong 18 giờ thì đầy bể. Nếu vòi 1 chảy trong 4 giờ, vòi 2 chảy trong 7 giờ thì chỉ được $\frac{1}{3}$ bể. Hỏi nếu mỗi vòi chảy một mình thì trong bao lâu sẽ đầy bể?

Hướng dẫn giải

Gọi x (bể) là phần nước của bể vòi một chảy được trong 1 giờ (x > 0)

y (bể) là phần nước của bể vòi hai chảy dược trong 1 giờ (y > 0)

Hai vòi nước cùng chảy vào một bể cạn trong 18 giờ thì đầy bể nên

18x + 18y = 1.(1)

Vòi 1 chảy trong 4 giờ, vòi 2 chảy trong 7 giờ thì chỉ được $\frac{1}{3}$ bể nên

4x + 7y = $\frac{1}{3}$.(2)

Từ (1) và (2) ta có hệ phương trình:

$\left\{\begin{array}{l}18x+18y=1\\ 4x+7y=\frac{1}{3}\end{array}\right.$

$\left\{\begin{array}{l}18x+18y=1\\ x=\frac{1}{4}\left(\frac{1}{3}-7y\right)\end{array}\right.$

$\left\{\begin{array}{l}\frac{18}{4}\left(\frac{1}{3}-7y\right)+18y=1\\ x=\frac{1}{4}\left(\frac{1}{3}-7y\right)\end{array}\right.$

$\left\{\begin{array}{l}\frac{-27}{2}y=-\frac{1}{2}\\ x=\frac{1}{4}\left(\frac{1}{3}-7y\right)\end{array}\right.$

$\left\{\begin{array}{l}y=\frac{1}{27}\\ x=\frac{1}{54}\end{array}\right.$(thỏa mãn điều kiện)

Ta có vòi 1 mỗi giờ chảy được $\frac{1}{54}$ bể suy ra vòi 1 chảy một mình 54 giờ thì đầy bể,

vòi 2 mỗi giờ chảy được $\frac{1}{27}$ bể suy ra vòi 2 chảy một mình 27 giờ thì đầy bể.

Vậy vòi 1 chảy một mình 54 giờ thì đầy bể, vòi 2 chảy một mình trong 27 giờ thì đầy bể.

Xem thêm các bài tóm tắt Lý thuyết Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 2: Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn

Lý thuyết Bài 3: Giải hệ hai phương trình bậc nhất hai ẩn

Lý thuyết Bài 1: Bất đẳng thức

Lý thuyết Bài 2: Bất phương trình bậc nhất một ẩn

Lý thuyết Bài 1: Căn bậc hai

Lý thuyết Bài 2: Căn bậc ba