Với tóm tắt lý thuyết Toán lớp 9 Bài 1: Căn bậc hai sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 1: Căn bậc hai

A. Lý thuyết Căn bậc hai

1. Căn bậc hai

Khái niệm căn bậc hai

Chú ý:

- Mỗi số dương a có đúng hai căn bậc hai là hai số đối nhau: số dương là $\sqrt{a}$ (căn bậc hai số học của a) và số âm là $-\sqrt{a}$.

- Số 0 chỉ có đúng một căn bậc hai là chính nó, ta viết $\sqrt{0}=0$.

- Số âm không có căn bậc hai.

- Phép toán tìm căn bậc hai số học của số không âm gọi là phép khai căn bậc hai hay phép khai phương (gọi tắt là khai phương).

­- Nếu $a>b>0$ thì $\sqrt{a}>\sqrt{b}$. Suy ra $-\sqrt{a}<-\sqrt{b}<0<\sqrt{b}<\sqrt{a}$.

Ví dụ:

• $\sqrt{81}=9$ nên 81 có hai căn bậc hai là 9 và -9.
• Căn bậc hai số học của 121 là $\sqrt{121}=11$.

2. Tính căn bậc hai của một số bằng máy tính cầm tay

Ví dụ:

Bấm lần lượt các phím  ta tính được $\sqrt{9,45}\approx 3,07$.

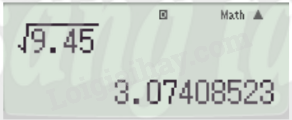
Vậy căn bậc hai của 9,45 (làm tròn đến chữ số thập phân thứ hai) là 3,07 và -3,07.

Tính chất của căn bậc hai

Ví dụ: $\sqrt{{\left(1+\sqrt{2}\right)}^2}=\left|1+\sqrt{2}\right|=1+\sqrt{2}$; $\sqrt{{\left(-3\right)}^2}=\left|-3\right|=3$.

3. Căn thức bậc hai

Khái niệm căn thức bậc hai

Ví dụ: $\sqrt{2x-1}$, $\sqrt{-\frac{1}{3}x+2}$ là các căn thức bậc hai.

Chú ý:

- Ta cũng nói $\sqrt{A}$ là một biểu thức. Biểu thức $\sqrt{A}$ xác định (hay có nghĩa) khi A nhận giá trị không âm.

- Khi A nhận giá trị không âm nào đó, khai phương giá trị này ta nhận được giá trị tương ứng của biểu thức $\sqrt{A}$.

Ví dụ:

+ Căn thức $\sqrt{2x+1}$ xác định khi $2x+1\ge 0$ hay $x\ge -\frac{1}{2}$.

Tại $x=4$ thì $\sqrt{2.4+1}=\sqrt{9}=\sqrt{3^2}=3$.

+ Giá trị của biểu thức $\sqrt{b^2-4ac}$ tại $a=3;b=10;c=3$ là:

  $\sqrt{{10}^2-\mathrm{4.3.3}}=\sqrt{100-36}=\sqrt{64}=\sqrt{8^2}=8$.

Sơ đồ tư duy Căn bậc hai

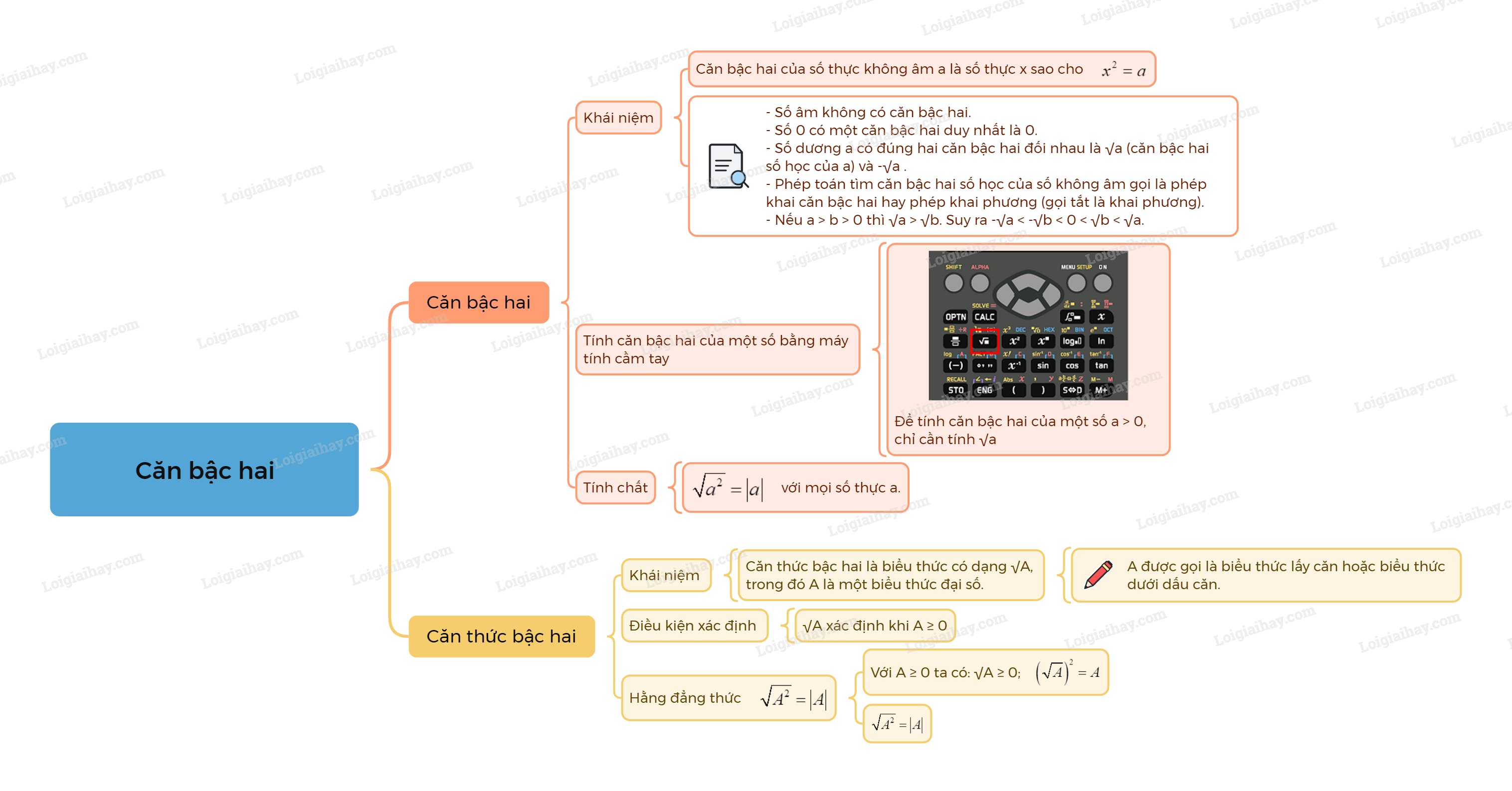
B. Bài tập Căn bậc hai

Bài 1. Tính:

Hướng dẫn giải

a) Ta có 10² = 100 nên $\sqrt{100}=10.$

b) Ta có 18² = 324 nên $\sqrt{324}=18.$

c) Ta có ${\left(\frac{3}{5}\right)}^2=\frac{9}{25}$ nên $\sqrt{\frac{9}{25}}=\frac{3}{5}.$

d) Ta có (0,4)² = 0,16 nên $\sqrt{0,16}=0,4.$

Bài 2. Tìm x, biết:

a) x² = 144;

b) 2x² = 8;

c) 3x² = 10.

Hướng dẫn giải

a) Ta có 12² = 144 nên x = 12 hoặc x = −12.

b) Ta có 2x² = 8 suy ra x² = 4. Mà 2² = 4 nên x = 2 hoặc x = −2.

c) Ta có 3x² = 10 suy ra $x^2=\frac{10}{3}.$ Mà ${\left(\sqrt{\frac{10}{3}}\right)}^2=\frac{10}{3}$ nên $x=\frac{10}{3}$ hoặc $x=-\frac{10}{3}.$

Bài 3. Cho biểu thức $A=\sqrt{x^2-2xy+2}.$ Tính giá trị của A khi:

a) x = 2, y = −3.

b) x = 1, y = 5.

c) x = −4, y = 4.

Hướng dẫn giải

a) Khi x = 2 và y = −3, ta có $A=\sqrt{2^2-\mathrm{2.2.}\left(-3\right)+2}=\sqrt{18}=3\sqrt{2}.$

b) Khi x = 1 và y = 5, ta có $A=\sqrt{1^2-\mathrm{2.1.5}+2}=\sqrt{-7}$ (không xác định vì −7 < 0).

c) Khi x = −4 và y = 4, ta có $A=\sqrt{4^2-\mathrm{2.4.4}+2}=\sqrt{-14}$ (không xác định vì −14 < 0).

Xem thêm các bài tóm tắt Lý thuyết Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 2: Bất phương trình bậc nhất một ẩn

Lý thuyết Bài 1: Căn bậc hai

Lý thuyết Bài 2: Căn bậc ba

Lý thuyết Bài 3: Tính chất của phép khai phương

Lý thuyết Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Lý thuyết Bài 1: Tỉ số lượng giác của góc nhọn