Với giải Thực hành 5 trang 70 Chuyên đề Toán 12 Chân trời sáng tạo chi tiết trong Bài 2: Phân bố Bernoulli và phân bố nhị thức giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Chuyên đề Toán 12. Mời các bạn đón xem:

Giải Chuyên đề Toán 12 Bài 2: Phân bố Bernoulli và phân bố nhị thức

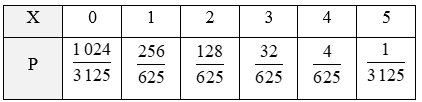
Thực hành 5 trang 70 Chuyên đề Toán 12: Cho biến ngẫu nhiên rời rạc X có phân bố nhị thức B(5; 0,2).

a) Tính xác suất của biến cố “X lớn hơn 3”.

b) Tính kì vọng và độ lệch chuẩn của X.

Lời giải:

Ta có $P\left(X=k\right)=C_5^k\cdot 0,2^k\cdot {\left(1-0,2\right)}^{5-k}=C_5^k\cdot 0,2^k\cdot 0,8^{5-k},$ với k = 0, 1, 2, 3, 4, 5.

Lần lượt tính P(X = k) với k = 0, 1, 2, 3, 4, 5 từ công thức trên, ta thu được bảng phân bố xác suất của X như sau:

a) Xác suất của biến cố “X lớn hơn 3” là:

$P\left(X>3\right)=P\left(X=4\right)+P\left(X=5\right)=\frac{4}{625}+\frac{1}{3125}=\frac{21}{3125}.$

b) Kì vọng của X là:

$E\left(X\right)=0\cdot \frac{1024}{3125}+1\cdot \frac{256}{625}+2\cdot \frac{128}{625}+3\cdot \frac{32}{625}+4\cdot \frac{4}{625}+5\cdot \frac{1}{3125}=1.$

Phương sai của X là:

$V\left(X\right)=0^2\cdot \frac{1024}{3125}+1^2\cdot \frac{256}{625}+2^2\cdot \frac{128}{625}+3^2\cdot \frac{32}{625}+4^2\cdot \frac{4}{625}+5^2\cdot \frac{1}{3125}-1^2=\frac{4}{5}.$

Độ lệch chuẩn của X là:

$\sigma \left(X\right)=\sqrt{V\left(X\right)}=\sqrt{\frac{4}{5}}=\frac{2\sqrt{5}}{5}.$

Chú ý: Ta cũng có thể tính kì vọng và phương sai của X như sau:

E(X) = np = 5 . 0,2 = 1 và V(X) = np(1 – p) = 5 . 0,2 . (1 – 0,2) = 0,8.

Do đó độ lệch chuẩn của X là: $\sigma \left(X\right)=\sqrt{V\left(X\right)}=\sqrt{0,8}=\frac{2\sqrt{5}}{5}.$