Với giải HĐ 4 trang 42 Toán lớp 7 Kết nối tri thức với cuộc sống chi tiết trong Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc
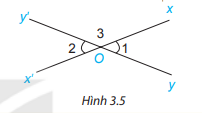
HĐ 4 trang 42 Toán lớp 7: Cho hai đường thẳng xx’ và yy’ cắt nhau tại O (H.3.5)
a) Dự đoán xem hai góc xOy và x’Oy’ có bằng nhau không?
b) Đo rồi so sánh số đo hai góc xOy và x’Oy’
Phương pháp giải:
Đo 2 góc rồi so sánh
Lời giải:
a) Em dự đoán xem hai góc xOy và x’Oy’ có bằng nhau.
b) Góc xOy = góc x’Oy’ =
Lý thuyết Góc ở vị trí đặc biệt
a) Hai góc kề bù
• Định nghĩa: Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là hai góc kề bù.
• Tính chất: Hai góc kề bù có tổng số đo bằng 180°.
Ví dụ:
+ Góc và có cạnh Oy chung; Ox và Oz là hai tia đối nhau. Do đó và được gọi là hai góc kề bù.
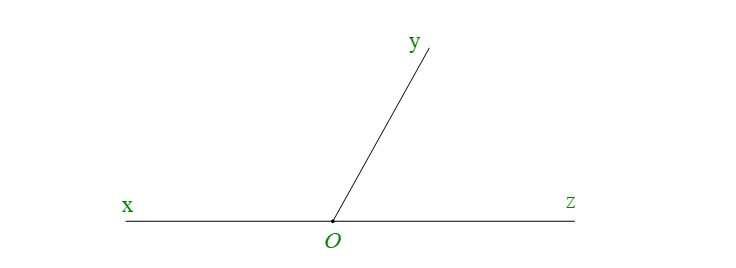
+ Vì và là hai góc kề bù nên .
Chú ý:
• Hai góc kề bù được hiểu là hai góc vừa kề nhau, vừa bù nhau. Trong đó:
- Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm khác phía nhau đối với đường thẳng chứa cạnh chung đó.
Ví dụ: Trong hình vẽ dưới đây, góc mOt và góc nOt là hai góc kề nhau.
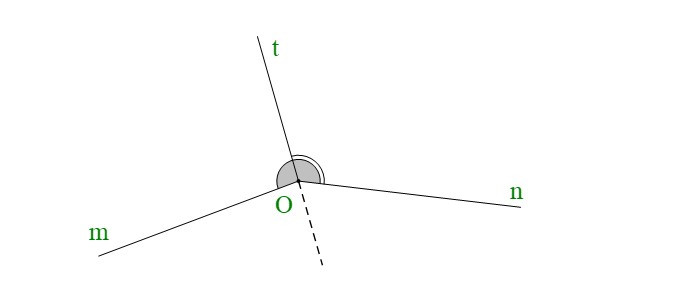
- Hai góc bù nhau là hai góc có tổng số đo bằng 180°.
Ví dụ: Trong hình vẽ dưới đây, có . Ta nói và là hai góc bù nhau.
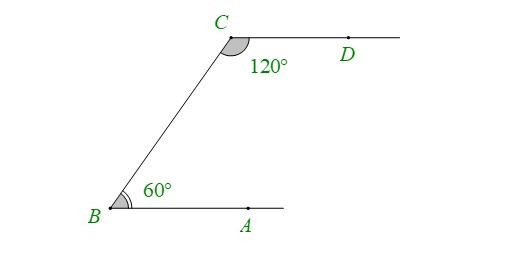
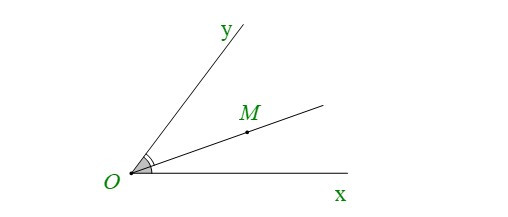
• Nếu điểm M nằm trong góc xOy thì ta nói tia OM nằm giữa hai cạnh (hai tia) Ox và Oy của góc xOy. Khi đó ta có:
b) Hai góc đối đỉnh
• Định nghĩa: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
• Tính chất: Hai góc đối đỉnh thì bằng nhau.
Ví dụ:
+ Hai đường thẳng , cắt nhau tại O. Khi đó và là hai tia đối nhau; và là hai tia đối nhau. Nên ta có các cặp góc đối đỉnh là: và ; và .
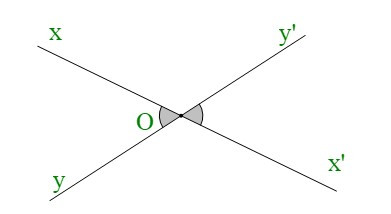
+ Có và là hai góc đối đỉnh thì ;
Ta lại có và là hai góc đối đỉnh thì .
Chú ý:
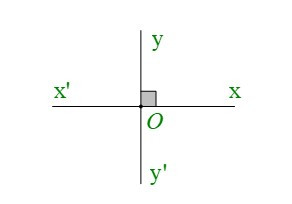
• Hai đường thẳng , cắt nhau và trong các góc tạo thành có một góc vuông được gọi là hai đường thẳng vuông góc. Kí hiệu là: .
Ví dụ: Hai đường thẳng , cắt nhau tại O sao cho thì .
Xem thêm các bài giải Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc
Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết
Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song