Tailieumoi.vn giới thiệu Giải bài tập Toán 8 Bài 2: Nhân đa thức với đa thức, chi tiết nhất giúp học sinh dễ dàng làm bài tập Nhân đa thức với đa thức lớp 8.
Lời giải:
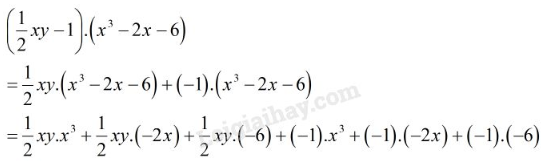
Phương pháp giải:
- Áp dụng quy tắc nhân đa thức với đa thức:
- Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
Lời giải:
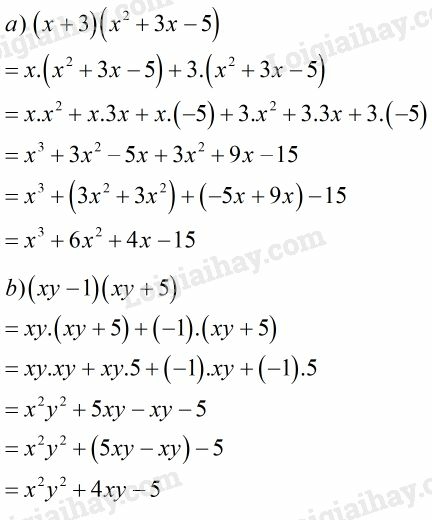
Áp dụng: Tính diện tích hình chữ nhật khi mét và mét.
Phương pháp giải:
Áp dụng:
- Công thức tính diện tích hình chữ nhật
- Quy tắc nhân đa thức với đa thức.
- Thay và vào biểu thức tìm được để tính giá trị của .
Lời giải:
Biểu thức tính diện tích hình chữ nhật là:
Áp dụng:
Khi mét và mét ta có:
Vậy diện tích của hình chữ nhật là
Câu hỏi và bài tập (trang 8, 9 sgk Toán 8 Tập 1)
Trả lời câu hỏi 7 trang 9 sgk Toán 8 Tập 1:Làm tính nhân:
a) ;
b)
Từ câu b), hãy suy ra kết quả phép nhân:
.
Phương pháp giải:
Áp dụng:
- Qui tắc nhân đa thức với đa thức.
- Qui tắc phá dấu ngoặc: -(b-a)=-b+a=a-b
Lời giải:
a)
b)
Ta có:
Suy ra kết quả của phép nhân:
a)
b)
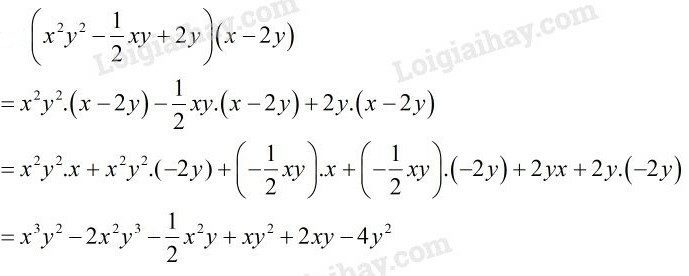
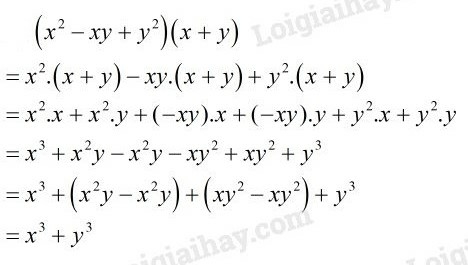
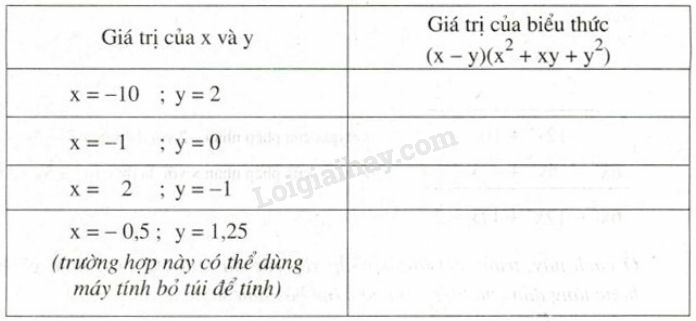
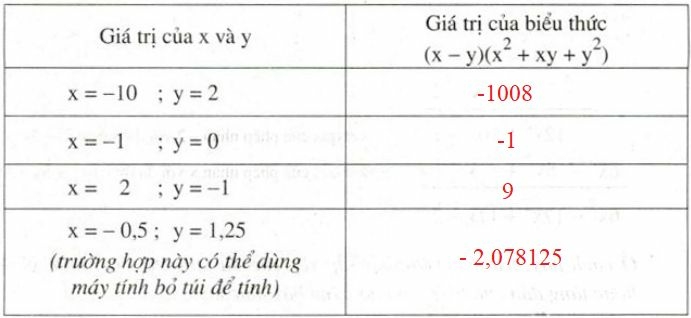
Trước hết, ta làm tính nhân để rút gọn biểu thức, ta được:
Sau đó tính giá trị của biểu thức:
Ta có:
Khi thì
Khi thì
Khi thì
Khi thì
a)
b)
Phương pháp giải:
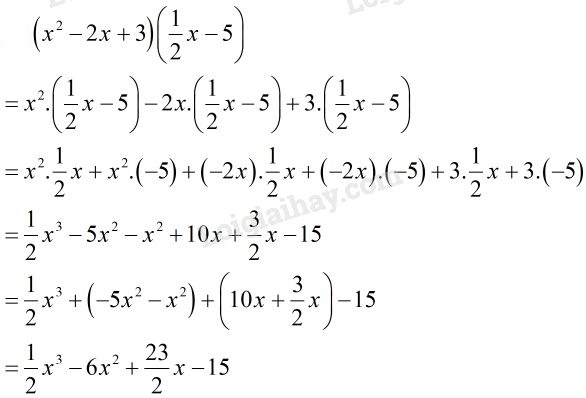
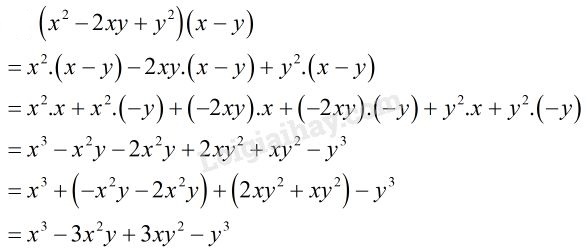
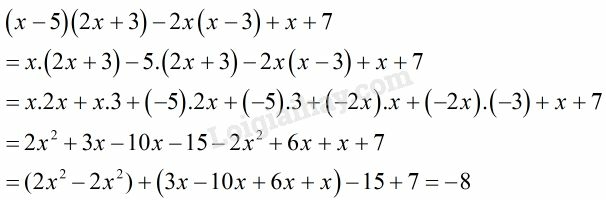
a) b)
c) d)
Lời giải:
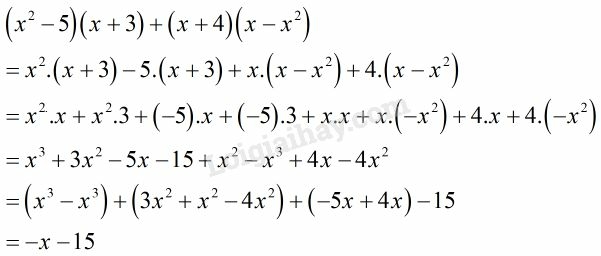
a) Với giá trị của biểu thức đã cho là:
b) Với giá trị của biểu thức đã cho là:
c) Với giá trị của biểu thức đã cho là:
d) Với giá trị của biểu thức đã cho là:
Gọi ba số chẵn liên tiếp là
Tích hai số sau là:
Tích hai số đầu là:
Theo đề bài tích của hai số sau lớn hơn tích của hai số đầu là nên ta có:
(thỏa mãn điều kiện)
Vậy ba số đó là
a)
b)
Lời giải:
a)
b)
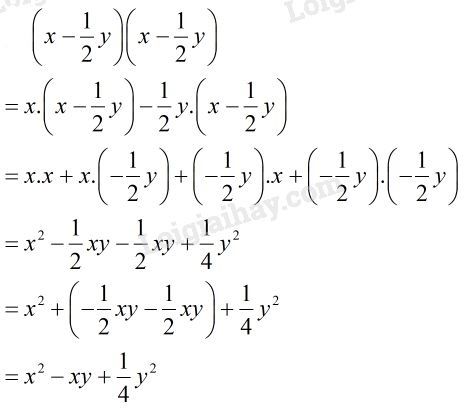
Lý thuyết nhân đa thức với đa thức
1. Qui tắc nhân đa thức với đa thức: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
2. Công thức: Cho là các đa thức ta có:
3. Các dạng toán cơ bản
Dạng 1: Thực hiện phép tính (hoặc rút gọn biểu thức)
Phương pháp:
Sử dụng quy tắc nhân đa thức với đa thức.
Ví dụ:
Dạng 2: Tính giá trị biểu thức
Phương pháp:
Giá trị của biểu thức tại là
Ví dụ:
Tính giá trị của biểu thức:
tại
Ta có:
Tại ta có: .
Dạng 3: Tìm
Phương pháp:
Sử dụng các quy tắc nhân đa thức với đa thức để biến đổi đưa về dạng tìm cơ bản.
Ví dụ:
Tìm x biết:
Ta có: