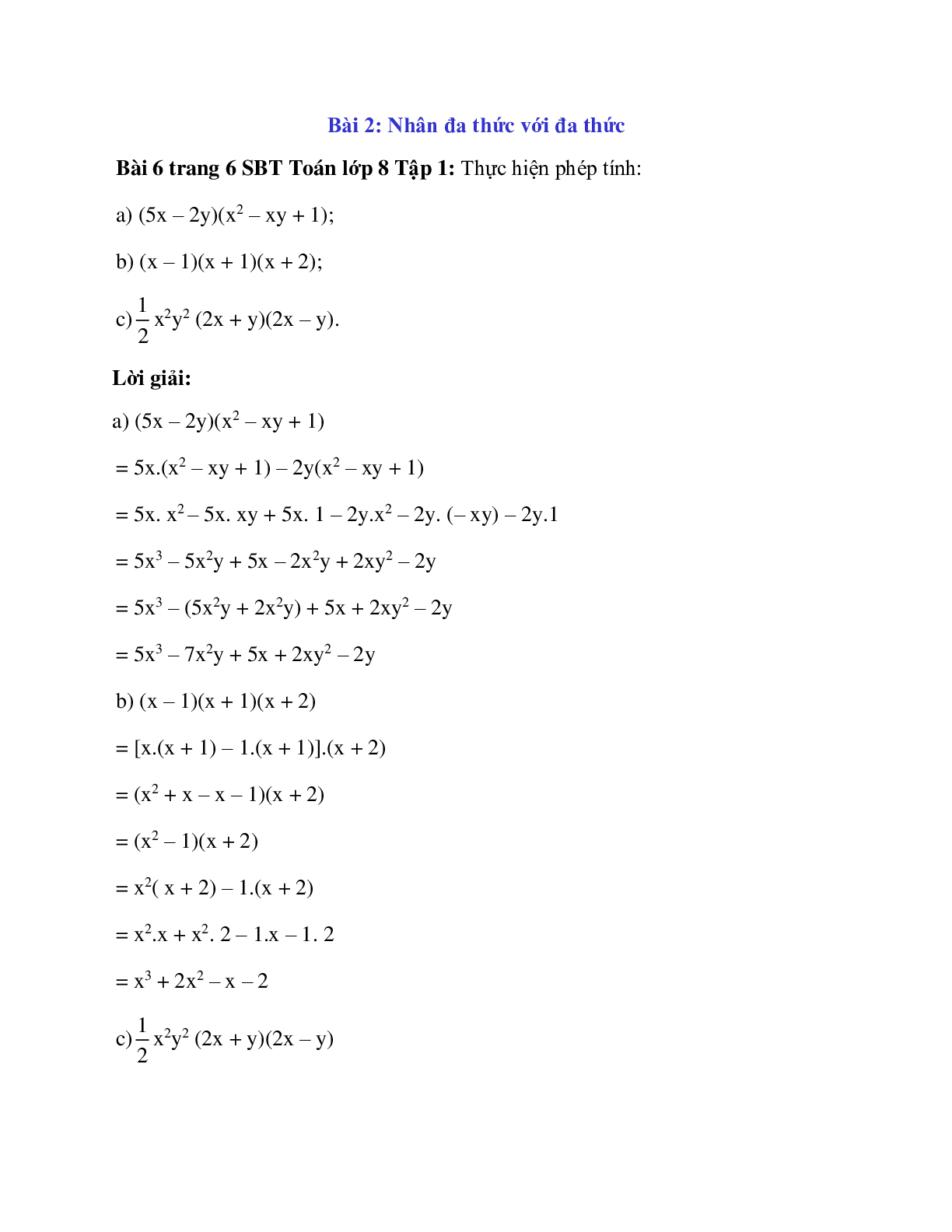Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh lớp 8 tài liệu giải sách bài tập Toán lớp 8 Bài 2: Nhân đa thức với đa thức chi tiết được Giáo viên nhiều năm kinh nghiệm biên soạn bám sát nội dung sách bài tập Toán 8 Tập 1 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. 

Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu tác phẩm Giải SBT Toán 8 Bài 2: Nhân đa thức với đa thức:

Giải SBT Toán 8 Bài 2: Nhân đa thức với đa thức

Bài 6 trang 6 SBT Toán lớp 8 Tập 1: Thực hiện phép tính:

a) (5x – 2y)(x² – xy + 1);

b) (x – 1)(x + 1)(x + 2);

c) $\frac{1}{2}$x²y² (2x + y)(2x – y).

Lời giải:

a) (5x – 2y)(x² – xy + 1)

= 5x.(x² – xy + 1) – 2y(x² – xy + 1)

= 5x. x² – 5x. xy + 5x. 1 – 2y.x² – 2y. (– xy) – 2y.1

= 5x³ – 5x²y + 5x – 2x²y + 2xy² – 2y

= 5x³ – (5x²y + 2x²y) + 5x + 2xy² – 2y

= 5x³ – 7x²y + 5x + 2xy² – 2y

b) (x – 1)(x + 1)(x + 2)

= [x.(x + 1) – 1.(x + 1)].(x + 2)

= (x² + x – x – 1)(x + 2)

= (x² – 1)(x + 2)

= x²( x + 2) – 1.(x + 2)

= x².x + x². 2 – 1.x – 1. 2

= x³ + 2x² – x – 2

c) $\frac{1}{2}$x²y² (2x + y)(2x – y)

= $\frac{1}{2}$.x²y² [2x .(2x – y) + y. (2x – y)]

= $\frac{1}{2}$.x²y² (4x² – 2xy + 2xy – y²)

= $\frac{1}{2}$.x²y² (4x² – y²)

= $\frac{1}{2}$.x².y².4x² + $\frac{1}{2}$.x²y². (– y²)

= 2x⁴y² – $\frac{1}{2}$x²y⁴

Bài 7 trang 6 SBT Toán 8 Tập 1: Thực hiện phép tính:

a) ( $\frac{1}{2}$x – 1)(2x – 3);

b) (x – 7)(x – 5);

c)(x – $\frac{1}{2}$ )(x + $\frac{1}{2}$)(4x – 1).

Lời giải:

a)( $\frac{1}{2}$x – 1) (2x – 3)

= $\frac{1}{2}$ x. (2x – 3) – 1.(2x – 3)

= $\frac{1}{2}$x. 2x + $\frac{1}{2}$ x. (–3) – 1.2x – 1. (– 3)

= x² –  $\frac{3}{2}$x – 2x + 3

= x² – ( $\frac{3}{2}$x + 2x ) + 3

= x² –  $\frac{7}{2}$x + 3

b) (x – 7)(x – 5)

= x. (x – 5) – 7.(x – 5)

= x² – 5x – 7x + 35

= x² – (5x + 7x) + 35

= x² – 12x + 35

c)(x – $\frac{1}{2}$)(x + $\frac{1}{2}$ )(4x – 1)

=[x. (x + $\frac{1}{2}$)  – $\frac{1}{2}$ .(x + $\frac{1}{2}$)]. (4x – 1)

= (x² + $\frac{1}{2}$x – $\frac{1}{2}$x – $\frac{1}{4}$ ).(4x – 1)

= (x² –  $\frac{1}{4}$)(4x – 1)

= x².(4x – 1) – $\frac{1}{4}$(4x – 1).

= 4x³ – x² – x + $\frac{1}{4}$

Bài 8 trang 6 SBT Toán 8 Tập 1: Chứng minh:

a) (x – 1)(x² + x + 1) = x³ – 1;

b) (x³ + x²y + xy² + y³)(x – y) = x⁴ – y⁴.

Lời giải:

a) Ta có: VT = (x – 1)(x² + x + 1)

= x.(x² + x + 1) + (– 1)(x² + x + 1)

= x³ + x² + x – x² – x – 1

= x³ + (x² – x²) + (x – x) – 1

= x³ – 1 = VP (điều phải chứng minh)

Vậy (x – 1)(x² + x + 1) = x³ – 1.

b) Ta có: VT = (x³ + x²y + xy² + y³)(x – y)

= (x – y). (x³ + x²y + xy² + y³).

= x. (x³ + x²y + xy² + y³ ) – y(x³ + x²y + xy² + y³)

= x⁴ + x³y + x²y² + xy³ – x³y – x²y² – xy³ – y⁴

= x⁴ + (x³y – x³y) + (x²y² – x²y²) + (xy³ – xy³) – y⁴

= x⁴ – y⁴ = VP (điều phải chứng minh)

Vậy (x³ + x²y + xy² + y³)(x – y) = x⁴ – y⁴

Bài 9 trang 6 SBT Toán 8 Tập 1: Cho a và b là hai số tự nhiên. Biết a chia cho 3 dư 1; b chia cho 3 dư 2. Chứng minh rằng ab chia cho 3 dư 2.

Lời giải:

Ta có: a chia cho 3 dư 1 nên a = 3q + 1 (q ∈ $\mathrm{\mathbb{N}}$)

b chia cho 3 dư 2 nên b = 3k + 2 (k ∈ $\mathrm{\mathbb{N}}$ )

Suy ra: a.b = (3q + 1)(3k + 2) = 3q(3k + 2) + 1. (3k + 2) = 9qk + 6q + 3k + 2

Vì 9 ⁝ 3 nên 9qk ⁝ 3

Vì 6 ⁝ 3 nên 6q ⁝ 3

Vì 3 ⁝ 3 nên 3k ⁝ 3

Và 2 chia cho 3 dư 2.

Vậy a.b = 9qk + 6q + 3k + 2 = 3(3qk + 2q + k) + 2 chia cho 3 dư 2 ( điều phải chứng minh).

Bài 10 trang 6 SBT Toán 8 Tập 1: Chứng minh rằng biểu thức n(2n – 3) – 2n(n + 1) luôn chia hết cho 5 với mọi số nguyên n.

Lời giải:

Ta có: n(2n – 3) – 2n(n + 1)

= n.2n + n. (– 3) – 2n.n – 2n. 1

= 2n² – 3n – 2n² – 2n

=(2n² – 2n²) – (3n + 2n)

= – 5n

Vì –5 ⁝ 5 nên – 5n ⁝ 5 với mọi n $\in \mathrm{\mathbb{Z}}$ (điều phải chứng minh).

Bài tập bổ sung

Bài 2.1 trang 6 SBT Toán 8 Tập 1: Kết quả của phép tính (x − 5)(x + 3) là:

(A). x² – 15;

(B). x² − 8x – 15;

(C). x² + 2x – 15;

(D). x² − 2x – 15.

Hãy chọn kết quả đúng.

Lời giải:

Chọn D.

Ta có: (x − 5)(x + 3)

= x(x + 3) – 5( x + 3)

= x² + 3x – 5x – 15

= x² – (5x – 3x) – 15

= x² − 2x − 15

Bài 2.2 trang 6 SBT Toán 8 Tập 1: Chứng minh rằng giá trị của biểu thức (n − 1)(3 − 2n) − n(n + 5) chia hết cho 3 với mọi giá trị của n.

Lời giải:

Ta có: (n − 1)(3 − 2n) − n(n + 5)

= n(3 – 2n) – 1.(3 – 2n) – n.n – n.5

= 3n − 2n² – 3 + 2n − n² − 5n

= (– 2n² – n²) + (3n + 2n – 5n) – 3

= −3n² – 3 = −3(n² + 1).

Vì – 3 ⁝ 3 nên – 3(n² +1) ⁝ 3 với mọi giá trị của n. (điều phải chứng minh).

Vậy biểu thức chia hết cho 3 với mọi giá trị của n.