Giải SBT Toán 8 trang 104 Tập 1 Cánh diều

Nguyễn Mạnh Tài Ngày: 17-11-2023 Lớp 8

708

Với lời giải SBT Toán 8 trang 104 Tập 1 Bài tập cuối chương 5 trang 103 sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài tập cuối chương 5 trang 103

Bài 41 trang 104 SBT Toán 8 Tập 1: Cho tam giác $A B C$ vuông tại $A$ có đường cao $A H$ . Kẻ $H J$ vuông góc với $A B$ tại $J$ và $H K$ vuông góc với $A C$ tại $K$ . Trên tia $H J$ lấy điểm $D$ sao cho $D J = J H$ . Trên tia $H K$ lấy điểm $E$ sao cho $E K = K H$ .

a) Chứng minh $A$ là trung điểm của $D E$ .

b) Tứ giác $A J H K$ là hình gì? Vì sao?

c) Chứng minh $B C = B D + C E$ .

Lời giải:

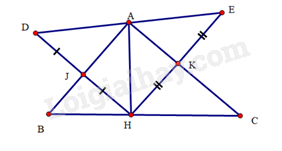
Sách bài tập Toán 8 (Cánh diều) Bài tập cuối chương 5 trang 103 (ảnh 3)

a) Xét $Δ A D J$ vuông tại $J$ và $Δ A H J$ vuông tại $J$ có:

$D J = H J$ (gt), $A J$ là cạnh chung

Do đó $Δ A D J = Δ A H J$ (hai cạnh góc vuông)

Suy ra $A D = A H$ (hai cạnh tương ứng) và $\hat{J A D} = \hat{J A H}$ (hai góc tương ứng)

Tương tự ta cũng chứng minh được $Δ A H K = Δ A E k$ (hai cạnh góc vuông)

Suy ra $A H = A E$ (hai cạnh tương ứng) và $\hat{K A H} = \hat{K A E}$ (hai góc tương ứng)

Ta có:

$\hat{J A D} + \hat{J A H} + \hat{K A H} + \hat{K A E} = 2 (\hat{J A H} + \hat{K A H}) = 2. \hat{J A K} = {2.90}^{\circ} = 180^{\circ}$

Hay $\hat{D A E} = 180^{\circ}$ nên ba điểm $D, A, E$ thẳng hàng

Lại có $A D = A H$ và $A H = A E$ nên $A D = A E$

Do đó $A$ là trung điểm của $D E$ .

b) Ta có $A B ⊥ H E$ tại $K$ nên $\hat{A J H} = 90^{\circ}$

$A C ⊥ H E$ tại $K$ nên $\hat{A K H} = 90^{\circ}$

Xét tứ giác $A J K H$ có:

$\hat{A J H} = \hat{J A K} = \hat{A K H} = 90^{\circ}$ nên là hình chữ nhật.

c) Xét tam giác $B D J$ vuông tại $J$ và tam giác $B H J$ vuông tại $J$ có:

$D J = H J$ (gt), $B J$ là cạnh chung

Do đó $Δ B D J = Δ B H J$ (hai cạnh góc vuông)

Suy ra $B D = B H$ (hai cạnh tương ứng)

Tương tự, ta cũng có $Δ C H K = Δ C E K$ (hai cạnh góc vuông)

Suy ra $C H = C E$ (hai cạnh tương iwnsg)

Khi đó $B C = B H + C H = B D + C E$

Vậy $B C = B D + C E$ .

Bài 42 trang 104 SBT Toán 8 Tập 1: Cho hình thang cân $A B C D$ có $A B / / C D, \hat{D} = 45^{\circ}$ . Kẻ $A H$ vuông góc với $C D$ tại $H$ . Lấy điểm $E$ thuộc cạnh $C D$ sao cho $H E = D H$ .

a) Chứng minh tứ giác $A B C E$ là hình bình hành.

b) Đường thẳng qua null song song với $A E$ cắt $A H$ tại $F$ . Tứ giác $A D F E$ là hình gì? Vì sao?

c) Tìm điều kiện của hình thang cân $A B C D$ để $E$ là trung điểm của $B F$ (bỏ qua giả thiết $\hat{D} = 45^{\circ}$ ).

Lời giải:

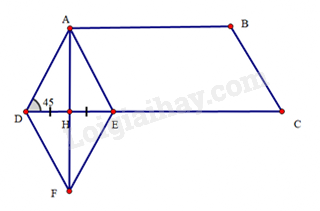
Sách bài tập Toán 8 (Cánh diều) Bài tập cuối chương 5 trang 103 (ảnh 4)

a) $Δ A D H = Δ A E H$ (cạnh góc vuông – cạnh góc vuông), suy ra $A D = A E$ (hai cạnh tương ứng)

Xét tứ giác $A B C E$ , ta có:

$A B / / E C$

Vì $A D = A E$ mà $A D = B C$ nên $A E = B C$

Vậy tứ giác $A B C E$ là hình bình hành.

b) Xét tam giác $A H E$ và $F H D$ , ta có:

$\hat{A E H} = \hat{F D H}$ (so le trong); $\hat{A H E} = \hat{F H D} = 90^{\circ}$ ; $D H = H E$

Suy ra $Δ A H E = Δ D H D$ (g.c.g)

Suy ra $A H = H F$

Xét tứ giác $A D E F$ , ta có:

$H D = H E; H A = H F$

Mà $A F ⊥ D E$

Suy ra tứ giác $A D E F$ là hình thoi.

c) Để $E$ là trung điểm của $B F$ thì $B E = F E$ và ba điểm $B, E, F$ thẳng hàng.

Khi bỏ qua giả thiết $\hat{A D C} = 45^{\circ}$ thì ta chứng minh được tứ giác $A D E F$ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên $A D E F$ là hình bình hành.

Do $A B C E$ và $A D E F$ đều là hình bình hành nên $A E = B C, A E / / B C$ và $A E = D F . A E / / D F$

Suy ra $B C = D F$ và $B C / / D F$

Tứ giác $B C F D$ có $B C = D F$ và $B C / / D F$ nên $B C F D$ là hình bình hành.

Mà $E$ là trung điểm của $B F$ , suy ra $E$ là trung điểm của $C D$ hay $E C = E D = \frac{1}{2} C D$ .

Mặt khác, $A B = E C$ (vì $A B C E$ là hình bình hành), suy ra $A B = \frac{1}{2} C D$

Dễ thấy nếu hình thang cân $A B C D (A B / / C D)$ có $A B = \frac{1}{2} C D$ thì $E$ là trung điểm của $B F$ .

Vậy điều kiện của hình thang cân $A B C D (A B / / C D)$ để $E$ là trung điểm của $B F$ là $A B = \frac{1}{2} C D$ .

Bài 43 trang 104 SBT Toán 8 Tập 1: Cho hình bình hành $A B C D$ có $B C = 2 A B$ . Gọi $M, N$ lần lượt là trung điểm của $B C, A D$

a) Chứng minh tứ giác $M B N D$ là hình bình hành.

b) Gọi $P$ là giao điểm của $A M$ và $B N, Q$ là giao điểm của $C N$ và $D M$ . Chứng minh tứ giác $P M Q N$ là hình chữ nhật.

c) Tìm điều kiện của hình bình hành $A B C D$ để tứ giác $P M Q N$ là hình vuông.

d) Tính diện tích của tứ giác $P M Q N$ , biết $A B = 2 c m, \hat{M A D} = 30^{\circ}$ .

Lời giải:

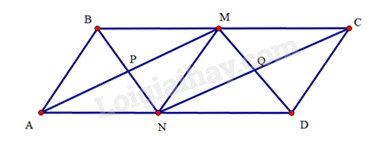
Sách bài tập Toán 8 (Cánh diều) Bài tập cuối chương 5 trang 103 (ảnh 5)

a) Do $A B C D$ là hình bình hành nên $B C / / A D$ và $B C = A D$

Mà $M \in B C, N \in A D$ nên $M B / / N D$

Lại có $M, N$ lần lượt là trung điểm của $B C, A D$ nên $M B = M C = \frac{1}{2} B C, N A = N D = \frac{1}{2} A$

Do đó $M B = M C = N A = N D$

Tứ goác $M B N D$ có $M B / / N D$ và $M B = N D$ nên là hình bình hành.

b) Tương tự câu a, ta chứng minh được $M A N C$ là hình bình hành.

Do $M B N D, M A N C$ đều là hình bình hành nên $P N / / M Q, P M / / N Q$ . Suy ra tứ giác $P M Q N$ là hình bình hành.

$Δ A B N = Δ M B N$ (c.g.c). Suy ra $A B = M N$ .

Tứ giác $A B M N$ có $A B = B M - M N = A N$ nên $A B M N$ là hình thoi. Suy ra $A M ⊥ B n$

Hình bình hành $P M Q N$ có $\hat{M P N} = 90^{\circ}$ nên $P M Q N$ là hình chữ nhật.

c) Để hình chữ nhật $P M Q N$ là hình vuông thì $P M = P N$ .

Mà $A B M N$ là hình thoi nên $A B M N$ là hình bình hành. Suy ra $A M, B N$ cắt nhau tại trung điểm $P$ của mỗi đường. mà $P M = P N$ , suy ra $A M = B N$

Hình bình hành $A B M N$ có $A M = B N$ nên $A B M N$ là hình chữ nhật

Suy ra $\hat{A B M} = 90^{\circ}$ hay $\hat{A B C} = 90^{\circ}$

Hình bình hành $A B C D$ có $\hat{A B C} = 90^{\circ}$ nên $A B C D$ là hình chữ nhật.

Dễ thấy, nếu hình bình hành $A B C D$ là hình chữ nhật và $B C = 2 A B$ thì $P M Q N$ là hình vuông.

Vậy điều kiện của hình bình hành $A B C D$ để $P M Q N$ là hình vuông là hình bình hành $A B C D$ là hình chữ nhật có $B C = 2 A B$ .

d) Ta có: $B M = A B$ nên $B M = 2 c m$

Do $A B M N$ là hình thoi nên $A M$ là tia phân giác của $\hat{B A N}$

Suy ra $\hat{B A N} = 2 \hat{M A D} = 60^{\circ}$

Tam giác $A B N$ có $A B = A N$ và $\hat{B A N} = 60^{\circ}$ nên tam giác $A B N$ đều.

Suy ra $B N = A N = A B = 2 c m$

Do $P$ là trung điểm của $B N$ nên $B P = N P = \frac{B N}{2} = 1 c m$

Trong tam giác $B M P$ vuông tại $P$ , ta có: $B M^{2} = B P^{2} + M P^{2}$

Suy ra $M P^{2} = B M^{2} - B P^{2} = 3$ . Do đó $M P = \sqrt{3}$ cm

Do $P M Q N$ là hình chữ nhật nên diện tích của $P M Q N$ là:

$M P . N P = \sqrt{3} .1 = \sqrt{3} (c m^{2})$ .

Bài 44 trang 104 SBT Toán 8 Tập 1: Cho hình vuông $A B C D$ . Lấy điểm $M$ thuộc đường chéo $B D$ . Kẻ $M E$ vuông góc với $A B$ tại $E$ , $M F$ vuông góc với $A D$ tại $F$ .

a) Chứng minh: $D E = C F; D E ⊥ C F$ .

b) Chứng minh ba đường thẳng $D E, B F, C M$ cùng đi qua một điểm.

c) Xác định vị trí của điểm $M$ trên đường chéo $B D$ để diện tích của tứ giác $A E M F$ lớn nhất.

Lời giải:

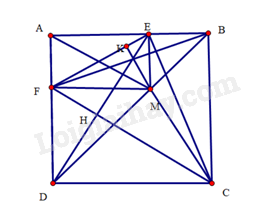
Sách bài tập Toán 8 (Cánh diều) Bài tập cuối chương 5 trang 103 (ảnh 6)

Gọi $H$ là giao điểm của $D E$ và $C F$ , $K$ là giao điểm của $C M$ và $E F$ .

Do $A B C D$ là hình vuông nên ta có:

$\hat{D A B} = 90^{\circ}, C D = D A, \hat{A D B} = \hat{A B D} = \hat{D B C} = 45^{\circ}$

a) Ta chứng minh được tam giác $F D M$ vuông cân tại $F$ .

Suy ra $F M = D F$

Tứ giác $A E M F$ có $\hat{M F A} = \hat{F A E} = \hat{A E M} = 90^{\circ}$ nên $A E M F$ là hình chữ nhật. Suy ra $A E = F M$ .

Do đó $A E = D F$ (vì cùng bằng $F M$ )

$Δ A D E = Δ D C F$ (c.g.c). Suy ra $D E = C F$ , $\hat{A E D} = \hat{D F C}$ .

Trong tam giác $A D E$ vuông tại $A$ , ta có: $\hat{A E D} + \hat{A D E} = 90^{\circ}$

Suy ra $\hat{D F C} + \hat{A D E} = 90^{\circ}$ hay $\hat{D F H} + \hat{F H D} = 90^{\circ}$ . Từ đó ta tính được $\hat{D H F} = 90^{\circ}$ . Vậy $D E ⊥ C F$ .

b) Tương tự câu a, ta chứng minh được $B F ⊥ C E$ .

$Δ A B M = Δ C B M$ (c.g.c). Suy ra $A M = C M$ . Mà $E F = A M$ (vì $A E M F$ là hình chữ nhật) suy ra $E F = C M$ .

$Δ D E F = Δ F C M$ (c.c.c). Suy ra $\hat{D E F} = \hat{F C M}$ hay $\hat{F E H} = \hat{F C K}$

Trong tam giác $H E F$ vuông tại $H$ , ta có $\hat{F E H} + \hat{E F H} = 90^{\circ}$

Suy ra $\hat{F C K} + \hat{E F H} = 90^{\circ}$ hay $\hat{F C K} + \hat{K F C} = 90^{\circ}$ . Từ đó, ta tính được $\hat{C K F} = 90^{\circ}$ . Do đó, $C K ⊥ E F$ .

Trong tam giác $C E F$ , ta có: $D E ⊥ C F, B F ⊥ C E, C M ⊥ E F$ nên ba đường thẳng $D E, B F, C M$ là các đường cao của tam giác $C E F$ . Vậy ba đường thẳng $D E, B F, C M$ cùng đi qua một điểm.

c) Chu vi của hình chữ nhật $A E M F$ là: $2 (A E + A F) = 2 (D F + A F) = 2 A D$

Mà $A D$ không đổi nên chu vi của hình chữ nhật $A E M F$ không đổi. Do đó, diện tích của tứ giác $A E M F$ lớn nhất khi $A E M F$ là hình vuông. Suy ra $M E = M F$ .