Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài 4: Khoảng cách trong không gian chi tiết sách Toán 11 Tập 2 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 4: Khoảng cách trong không gian
Lời giải:
Trong công trình này có: Khoảng cách giữa 2 điểm (d1), khoảng cách giữa 2 đường thẳng (d2), khoảng cách từ một điểm đếm một đường thẳng (d3), (d4) khoảng cách từ một điểm đến một mặt phẳng (d5).
Để đo những đường nằm ngang, ta có thể dùng thước dây, còn những đường nằm thẳng đứng thì dùng dây dọi.
1. Khoảng cách từ một điểm đến một đường thẳng, đến một mặt phẳng
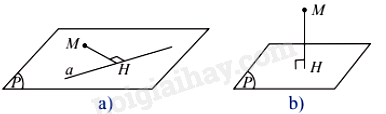
b) Cho điểm M không nằm trên mặt phẳng sàn nhà (P). Dùng dây dọi để tìm hình chiếu vuông góc H của M trên (P) (Hình 1a). Đo độ dài đoạn MH.
Lời giải:
a) Độ dài đoạn MH là khoảng cách từ điểm M đến đường thẳng a.
b) Độ dài đoạn MH là khoảng cách từ điểm M đến mặt phẳng P.
a) Tính khoảng cách từ B đến (SAD).
b) Tính khoảng cách từ A đến đường thẳng SC.
Lời giải:
a) Ta có:
d(B, (SAD)) = AB = a
b) Kẻ AH ⊥ SC.
Khi đó, d(A, SC) = AH.
• Tam giác ABC vuông tại B nên .
• Tam giác SAC vuông tại A nên .
• Tam giác SAC vuông tại A có đường cao AH nên .
Vậy d(A, SC)= .
Lời giải:
Đổi 20 cm = 0,2 m
Độ dài của cán quạt là: 3,6 − 2,5 − 0,2 = 0,9 (m)
Vậy phải làm cán quạt dài 0,9 m.
2. Khoảng cách giữa các đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song
Giải Toán 11 trang 76 Tập 2
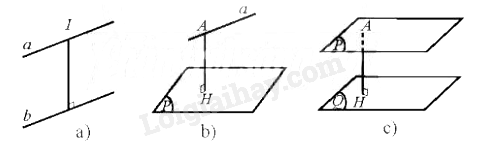
b) Cho hai mặt phẳng song song (P) và (Q) . Lấy hai điểm A, B tuỳ ý trên (P) và gọi H, K lần lượt là hình chiếu vuông góc của A và B trên (Q) (Hình 4b). So sánh độ dài hai đoạn thẳng AH và BK.
Lời giải:
a) Ta có:
Mà AB // HK ⇒ ABKH là hình bình hành có AH ⊥ (P)
⇒ ABKH là hình chữ nhật.
Vậy AH = BK.
b) Ta có:
Mà AB // HK ⇒ ABKH là hình bình hành có AH ⊥ (Q)
⇒ ABKH là hình chữ nhật.
Vậy AH = BK.
a) Giữa hai mặt phẳng (ACD′) và (A′C′B) ;
b) Giữa đường thẳng AB và (A′B′C′D′).
Lời giải:
a) Ta có
Gọi I là hình chiếu vuông góc của D trên OD′.
Ta có
và
• Xét tam giác ABD vuông tại A nên ta có:
• Xét tam giác D′DO vuông tại D có DI là đường cao nên
b) Ta có: AB // (A′B′C′D′).
Do đó d(AB, (A′B′C′D′)) = AA′ = a
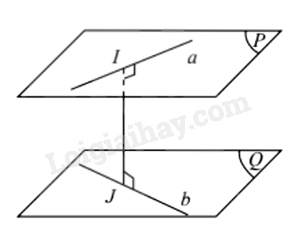
3. Khoảng cách giữa hai đường thẳng chéo nhau
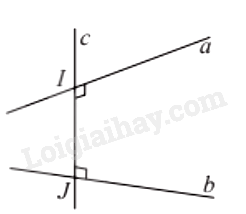
Đường thẳng IJ có vuông góc với b không? Giải thích.
Lời giải:
Ta có
Mà (P) ⊥(Q) ⇒ IJ ⊥ (Q) IJ ⊥ b
Tính khoảng cách giữa hai đường thẳng:
a) OA và BC;
b) OB và AC.
Lời giải:
a) Tam giác OBC vuông cân tại O. Gọi H là trung điểm của BC suy ra OH ⊥ BC
Ta lại có:
Do đó OH là đoạn vuông góc chung của OA và BC.
Khi đó
b)Tương tự trong tam giác OAC vuông cân tại O . Gọi K là trung điểm của AC.
Ta lại có:
Do đó OK là đoạn vuông góc chung của OB và AC.
Lời giải:
Vì trần nhà và sàn nhà song song với nhau nên đường thẳng a nằm trên trần nhà song song với sàn nhà.
Vậy khoảng cách giữa đường thẳng a trên trần nhà và đường thẳng b trên sàn nhà bằng khoảng cách giữa trần nhà và sàn nhà. Vậy d(a, b) = 3,2 m.
4. Công thức tính thể tích của khối chóp, khối lăng trụ, khối hộp
Lời giải:
Số hình lập phương đơn vị có trong hình hộp là: abc = 8.3.4 = 96 (hình).
Vậy số hình lập phương đơn vị có trong hình hộp là 96 hình.
Giải Toán 11 trang 79 Tập 2
Cho khối lăng trụ tam giác ABC.A′B′C′ (Hình 14). Tìm cách chia khối lăng trụ thành ba khối chóp có cùng chiều cao và diện tích đáy.
Lời giải:
Chia khối lăng trụ tam giác ABC.A′B′C′ thành ba khối chóp: A.A′B′C′, B′.ABC và C.A′B′C′.
Lời giải:
Diện tích đáy lớn là: S = 52 = 25 (m2)
Diện tích đáy bé là: S′ = 22 = 4 (m2)
Thể tích của bồn chứa là:
Lời giải:
Ta có khối nêm là lăng trụ đứng có đáy là tam giác vuông có các cạnh góc vuông lần lượt là 7cm và 24 cm.
Do đó diện tích đáy là:
Chiều cao của khối lăng trụ là h = 22 cm
Thể tích của khối nêm là: V = S.h = 84.22 = 1848 (cm3)
Bài tập
Lời giải:
Kẻ OI ⊥ CD, OH ⊥ SI
Ta có:
Mà OH ⊥ SI Suy ra OH ⊥ (SCD)
Do đó d(O, (SCD)) = OH.
Ta có: ΔABC đều AC = a
• Xét ΔABD, áp dụng định lí cos, ta có:
• Xét ΔOCD vuông tại O có OI là đường cao:
Ta có SO ⊥ (ABCD) SO ⊥ OI
Do đó, tam giác SOI vuông tại O có OH là đường cao nên
Vậy khoảng cách từ O đến mặt phẳng (SCD) là .
a) Chứng minh rằng AB ⊥ CD.
b) Xác định đoạn vuông góc chung của AB và CD.
Lời giải:
a) Gọi M là trung điểm của AB.
Ta có
b) Gọi H là hình chiếu vuông góc M của trên CD.
Ta có
Do đó MH là đoạn vuông góc chung của AB và CD.
a) Chứng minh AB ⊥ (SIJ).
b) Tính khoảng cách giữa hai đường thẳng AB và SC.
Lời giải:
a) Ta có: ΔSAB cân tại S và đáy là hình vuông ABCD.
b) Ta có: AB // CD ⇒ AB // (ABCD)
d(AB, SC) = d(AB, (SCD)) = d(I, (SCD))
Gọi H, K lần lượt là hình chiếu vuông góc của I, O trên SJ
Ta có
Vì AB // CD nên CD ⊥ (SIJ) CD ⊥ IH IH ⊥ (SCD)
d(AB, CD) = d(AB, (SCD)) = IH = 2OK
Ta có: ABCD là hình vuông
• Xét ΔSAO vuông tại O có
• Xét ΔSOJ vuông tại O có đường cao OK nên
Do đó .
a) Tính khoảng cách giữa hai đáy của hình lăng trụ.
b) Tính thể tích của khối lăng trụ.
Lời giải:
a) Vì khối lăng trụ đều nên gọi là trung điểm của BC AM ⊥ BC. Do đó góc giữa hai mặt phẳng ((A′BC), (ABC)) = .
Do đó khoảng cách giữa hai đáy của lăng trụ là:
b) Thể tích khối lăng trụ là:
Lời giải:
Vì tay vịn cầu song song với mặt đường nên khoảng cách giữa hai đường thẳng a và b
chính bằng khoảng cách từ đường thẳng a xuống mặt đường.
Khoảng cách giữa hai đường thẳng a và b bằng: 3,5 + 0,8 = 4,3(m).
Vậy khoảng cách giữa hai đường thẳng a và b là 4,3 m.
a) Tính khoảng cách giữa hai đường thẳng BD và AA′.
b) Tính thể tích của khối hộp.
Lời giải:
a) Vì hình hộp đứng có đáy ABCD là hình thoi tâm O.
Do đó ta có:
Suy ra là đoạn vuông góc chung của hai đường thẳng BD và AA'.
Do đó
b) Đáy ABCD là hình thoi tâm O có AB = a và
Do đó ta có:
Thể tích của khối hộp là:
Vậy thể tích của khối hộp là
a) Tính khoảng cách giữa hai đường thẳng AC và SB.
b) Tính thể tích của khối chóp.
Lời giải:
a) Kẻ OH ⊥ SB (H SB)
S.ABCD là hình chóp tứ giác đều SO ⊥ (ABCD) SO ⊥AC.
Tứ giác ABCD là hình vuông suy ra AC ⊥ BD AC ⊥(SBD) AC ⊥ OH.
Mà
Do đó d(AC, SB) = OH
• Xét ΔABD vuông tại A, ta có:
• Xét ΔSBO vuông tại O, ta có:
• Xét ΔSBO vuông tại O có SO = BO nên ΔSBO vuông cân tại O
Suy ra OH vừa là đường cao, vừa là đường trung tuyến.
Do đó
Vậy
b) .
Thể tích khối chóp là:
Lời giải:
Ta có mỗi hình lục giác đều được tạo bởi 6 tam giác đều có cạnh bằng cạnh của hình lục giác.
Do đó ta có diện tích các đáy là:
Chiều cao của khối chóp cụt là: h = OO′ = a
Thể tích khối chóp cụt là:
Vậy thể tích khối chóp cụt là
Xem thêm các bài giải SGK Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Hai mặt phẳng vuông góc
Bài 4: Khoảng cách trong không gian
Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
Bài 1: Biến cố giao và quy tắc nhân xác suất
Bài 2: Biến cố hợp và quy tắc cộng xác suất
Lý thuyết Khoảng cách trong không gian
1. Khoảng cách từ một điểm đến một đường thẳng, đến một mặt phẳng
Nếu H là hình chiếu vuông góc của điểm M trên đường thẳng a thì độ dài đoạn MH được gọi là khoảng cách từ M đến đường thẳng a, kí hiệu d(M, a).
Nếu H là hình chiếu vuông góc của điểm M trên mặt phẳng (P) thì độ dài đoạn MH được gọi là khoảng cách từ điểm M đến (P), kí hiệu d(M, (P)).
Quy ước:
Nhận xét:
a) Lấy điểm N tùy ý trên đường thẳng a, ta luôn có .
b) Lấy điểm N tùy ý trên mặt phẳng , ta luôn có .
2. Khoảng cách giữa các đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song
Khoảng cách giữa hai đường thẳng song song a và b là khoảng cách từ một điểm bất kì trên a đến b, kí hiệu d(a, b).
Khoảng cách giữa đường thẳng a đến mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì trên a đến (P), kí hiệu d(a, (P)).
Khoảng cách giữa hai mặt phẳng song song (P) và (Q) là khoảng cách từ một điểm bất kì trên (P) đến (Q), kí hiệu d((P), (Q)).
3. Khoảng cách giữa hai đường thẳng chéo nhau
Đường thẳng c vừa vuông góc, vừa cắt hai đường thẳng chéo nhau a và b được gọi là đường vuông góc chung của a và b.
Nếu đường vuông góc chung của hai đường thẳng chéo nhau a và b cắt chúng lần lượt tại I và J thì đoạn IJ gọi là đoạn vuông góc chung của a và b.
Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó, kí hiệu d(a, b)
Chú ý:
a) Khoảng cách giữa hai đường thẳng chéo nhau a và b bằng khoảng cách giữa một trong hai đường thẳng đến mặt phẳng song song với nó và chứa đường thẳng còn lại.
b) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.
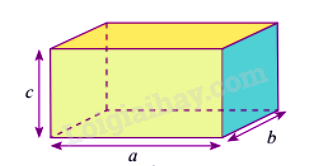
4. Công thức tính thể tích của khối chóp, khối lăng trụ, khối hộp
Thể tích khối hộp chữ nhật bằng ba kích thước:
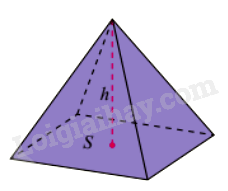
Thể tích khối chóp bằng một phần ba diện tích đáy nhân với chiều cao:
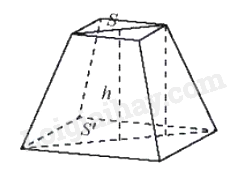
Thể tích khối chóp cụt đều có chiều cao h và diện tích hai đáy S, S’:
Thể tích khối lăng trụ bằng tích diện tích đáy và chiều cao: