Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện chi tiết sách Toán 11 Tập 2 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
• được gọi là góc hợp bởi đường thẳng d và (Q).
• được gọi là góc hợp bởi hai mặt phẳng (P) và (Q).
Lời giải:
K là hình chiếu vuông góc của C lên (Q) nên được gọi là góc hợp bởi đường thẳng d và (Q).
Ta có:
Nên được gọi là góc hợp bởi hai mặt phẳng (P) và (Q)
1. Góc giữa đường thẳng và mặt phẳng
Hoạt động khám phá 1 trang 82 Toán 11 Tập 2: Cho đường thẳng a và mặt phẳng (P).
a) Trong trường hợp a vuông góc với (P), tìm góc giữa a và một đường thẳng b tuỳ ý trong (P).
b) Trong trường hợp a không vuông góc với (P), tìm góc giữa a và đường thẳng a′ là hình chiếu vuông góc của a trên (P).
Lời giải:
a) Ta có:
b) Lấy A a. Gọi
Dựng AH ⊥ a′ (H a′)
Ta có:
a) AA′ ;
b) BC′ ;
c) A′C.
Lời giải:
a) AA′ ⊥ (ABCD) (AA′, (ABCD)) = 90°
b) CC′ ⊥ (ABCD) (BC′, (ABCD)) = (BC′, BC) =
c) AA′⊥(ABCD) (A′C, (ABCD)) = (A′C, AC) =
Vậy (A′C, (ABCD)) .
Lời giải:
• DK ⊥ (ABHK) ⇒ (BD, (ABHK)) = (BD, BK) =
• DK = CH = 2,
Vậy góc giữa đường thẳng BD và đáy hồ khoảng 33,3°.
2. Góc nhị diện và góc phẳng nhị diện
Lời giải:
Các nửa mặt phẳng có chung bờ d là: (P1),(P2),(Q1),(Q2).
Các nửa mặt phẳng này chia không gian thành 4 phần.
a) Nêu nhận xét về vị trí tương đối giữa d và mp(Ox,Oy).
b) Nêu nhận xét về số đo của góc khi O thay đổi trên d.
Lời giải:
a) Ta có:
b) Số đo của không đổi khi O thay đổi trên d.
a) [S, BC, O];
b) [C, SO, B].
Lời giải:
a) Gọi M là trung điểm BC.
ΔSBC đều ⇒ SM ⊥ BC
ΔOBC vuông cân tại O ⇒ OM ⊥ BC
Khi đó góc phẳng nhị diện [S, BC, O] = (MO, MS).
Ta có: O là trung điểm của BD, M là trung điểm của BC
⇒ OM là đường trung bình của ΔBCD
ΔSBC đều, M là trung điểm của BC
⇒ SM là đường trung tuyến
.
Suy ra [S, BC, O] = (MO, MS)
b) Ta có:
• SO ⊥ (ABCD) nên SO⊥OB
• SO ⊥ (ABCD) nên SO⊥OC
Vậy là góc phẳng nhị diện [C, SO, B].
Mà ABCD là hình vuông nên .
Vậy [C, SO, B] = 90o.
(Nguồn: https://en.wikipedia.org/wiki/Memphis_Pyramid)
Lời giải:
Mô hình hoá kim tự tháp bằng chóp tứ giác đều S.ABCD với O là tâm của đáy.
Vậy AB = 180 m, SO = 98 m.
Gọi M là trung điểm của BC.
• ΔSBC đều nên SM ⊥ BC.
• ΔOBC vuông cân tại O nên OM ⊥ BC.
Khi đó góc phẳng nhị diện [S, BC, O] = (MO, MS) = .
Ta có: O là trung điểm của BD, M là trung điểm của BC.
Suy ra OM là đường trung bình của ΔBCD.
Do đó .
Khi đó: .
Bài tập
Bài 1 trang 85 Toán 11 Tập 2: Cho tứ diện đều ABCD. Vẽ hình bình hành BCED.
a) Tìm góc giữa đường thẳng AB và (BCD).
b) Tìm góc phẳng nhị diện [A,CD,B]; [A,CD, E].
Lời giải:
a) Gọi I là trung điểm của CD, O là tâm của ΔBCD.
AO ⊥ (BCD)
(AB, (BCD)) = (AB, OB) =
Vậy góc giữa đường thẳng AB và (BCD) là .
b)
• ΔACD đều nên AI ⊥ CD
• ΔBCD đều nên BI ⊥ CD
Do đó .
Vậy là góc phẳng nhị diện [A, CD, B].
• ΔACD đều nên AI ⊥ CD
• ΔECD đều nên EI ⊥ CD
Do đó .
Vậy là góc phẳng nhị diện [A,CD, E].
a) Tìm góc giữa đường thẳng SA và (ABCD).
b) Tìm góc phẳng nhị diện [A, SO, B], [S, AB, O].
Lời giải:
a) S.ABCD là hình chóp tứ giác đều có O là tâm của đáy
SO ⊥ (ABCD) ⇒ (SA, (ABCD)) = (SA,OA) =
Vậy góc giữa đường thẳng SA và (ABCD) là
b) Gọi M là trung điểm của AB
SO ⊥ (ABCD) ⇒ SO ⊥ AO, SO ⊥ BO
Vậy là góc phẳng nhị diện [A, SO, B]
• ABCD là hình vuông nên
• ΔSAB đều nên SM ⊥ AB
• ΔOAB vuông cân tại O nên OM ⊥ AB
Vậy là góc phẳng nhị diện [S, AB, O].
a) Tìm góc giữa cạnh bên và mặt đáy.
b) Tìm góc phẳng nhị diện [O, AB, A′]; [O′, A′B′, A].
Lời giải:
a) Kẻ C′H ⊥ OC (H OC).
OO′C′H là hình chữ nhật nên OO′// C′H.
Mà OO′ ⊥ (ABCDEF) nên C′H ⊥ (ABCDEF).
Do đó (CC′, (ABCDEF)) = (CC′, CH) = .
b) Gọi M, M′ lần lượt là trung điểm của AB, A′B′.
Khi đó, OM ⊥ AB, O′M′ ⊥ A′B.
ABB′A′ là hình thang cân nên MM′ ⊥ AB, MM′ ⊥ A′B.
Do đó [O, AB, A′] = ; [O′, A′B′, A] = .
a) Tính số đo góc giữa đường thẳng CA′ và (CC′B′B).
b) Tính số đo góc nhị diện cạnh CC′.
Lời giải:
a) Xét tam giác vuông CBB′ có:
Gọi là góc giữa đường thẳng (CA′, (CC′B′B)) =
Khi đó: .
Suy ra .
b) Ta có: CC′ ⊥ (ABC) ⇒ CC′ ⊥ AC, CC′ ⊥ BC.
Gọi là góc phẳng nhị diện cạnh [A’, CC’, B’] = .
.
Suy ra
Lời giải:
Vì ABCD là hình vuông nên ta có OF = 7m
Chiều cao khối chóp S.ABCD là:
Tuơng tự có chiều cao khối chóp S.A′B′C′D′ là: SO′ = 5m
Thể tích khối chóp S.ABCD:
Thể tích khối chóp S.A’B’C’D’:
Thể tích khối chóp cụt bằng số khối đất phải đào:
.
Vậy có 290,6 m3 khối đất cần phải di chuyển ra khỏi hầm.
Xem thêm các bài giải SGK Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 4: Khoảng cách trong không gian
Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
Bài 1: Biến cố giao và quy tắc nhân xác suất
Bài 2: Biến cố hợp và quy tắc cộng xác suất
Lý thuyết Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
1. Góc giữa đường thẳng và mặt phẳng
Nếu đường thẳng a vuông góc với mặt phẳng (P) thì ta nói rằng góc giữa đường thẳng a và mặt phẳng (P) bằng .
Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa a và hình chiếu a’ của nó trên (P) được gọi là góc giữa đường thẳng a và mặt phẳng (P).
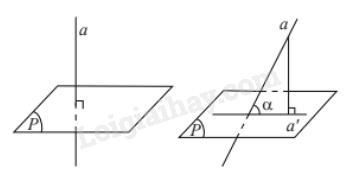
Chú ý:
a) Góc giữa đường thẳng và mặt phẳng luôn thỏa mãn .
b) Nếu đường thẳng a nằm trong (P) hoặc a song song với (P) thì .
2. Góc nhị diện và góc phẳng nhị diện
Góc nhị diện
Cho hai nửa mặt phẳng và có chung bờ là đường thẳng d. Hình tạo bởi , và d được gọi là góc nhị diện tạo bởi và , kí hiệu .
Hai nửa mặt phẳng , gọi là hai mặt của nhị diện và d gọi là cạnh của nhị diện.
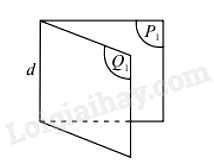
Chú ý:
a) Hai mặt phẳng cắt nhau theo giao tuyến d tạo thành bốn góc nhị diện.
b) Góc nhị diện còn được kí hiệu là với M, N tương ứng thuộc hai nửa mặt phẳng .
Góc phẳng nhị diện
Góc phẳng nhị diện của góc nhị diện là góc có đỉnh nằm trên cạnh của nhị diện, có hai cạnh lần lượt nằm trên hai mặt của nhị diện và vuông góc với cạnh của nhị diện.
Chú ý:
a) Đối với một góc nhị diện, các góc phẳng nhị diện đều bằng nhau.
b) Nếu mặt phẳng (R) vuông góc với cạnh d của góc nhị diện và cắt hai mặt của góc nhị diện theo hai nửa đường thẳng Ou và Ov thì là góc phẳng nhị diện của góc nhị diện tạo bởi .
c) Góc nhị diện có góc phẳng nhị diện là góc vuông được gọi là góc nhị diện vuông.
d) Số đo góc phẳng nhị diện được gọi là số đo góc nhị diện.
e) Số đo góc nhị diện nhận giá trị từ đến .