Giải Toán 11 trang 25 Tập 1 Chân trời sáng tạo

Giải Toán 11 trang 25 Tập 1 Chân trời sáng tạo

Nguyễn Mạnh Tài Ngày: 17-10-2023 Lớp 11

199

Với lời giải Toán 11 trang 25 Tập 1 chi tiết trong Bài 4: Hàm số lượng giác và đồ thị sách Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 Bài 4: Hàm số lượng giác và đồ thị

Hoạt động khởi động trang 25 Toán 11 Tập 1: Vì sao mặt cắt của sóng nước trên mặt hồ được gọi là có dạng hình sin?

Hoạt động khởi động trang 25 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Lời giải:

Sau khi học xong bài học này, chúng ta sẽ nhận biết được đồ thị hình sin và hình ảnh mặt cắt của sóng nước trên mặt hồ chính là một ví dụ điển hình.

1. Hàm số lượng giác

Hoạt động khám phá 1 trang 25 Toán 11 Tập 1: Cho số thực t và M là điểm biểu diễn của góc lượng giác có số đo t rad trên đường tròn lượng giác, hãy giải thích vì sao xác định duy nhất:

a) Giá trị sint và cost;

b) Giá trị tant (nếu $t \neq \frac{π}{2} + k π, k \in ℤ$ ) và cost (nếu $t \neq k π, k \in ℤ$ ).

Lời giải:

Hoạt động khám phá 1 trang 25 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Trên đường tròn lượng giác, điểm M là điểm biểu diễn góc lượng giác có số đo t, khi đó:

- Tung độ của điểm M là sint.

- Hoành độ của điểm M là cost.

Vì tung độ và hoành độ của điểm M là xác định duy nhất nên sint và cost xác định duy nhất.

b) Nếu $t \neq \frac{π}{2} + k π, k \in ℤ$ thì tan t = $\frac{\sin t}{cos t}$ xác định duy nhất vì sint và cost xác định duy nhất.

Nếu t $\neq$ k $π$ thì cot t = $\frac{cos t}{\sin t}$ xác định duy nhất vì sint và cost xác định duy nhất.

Video bài giảng Toán 11 Bài 4: Hàm số lượng giác và đồ thị - Chân trời sáng tạo

Xem thêm các lời giải bài tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Hoạt động khởi động trang 25 Toán 11 Tập 1: Vì sao mặt cắt của sóng nước trên mặt hồ được gọi là có dạng hình sin?...

Hoạt động khám phá 1 trang 25 Toán 11 Tập 1: Cho số thực t và M là điểm biểu diễn của góc lượng giác có số đo t rad trên đường tròn lượng giác, hãy giải thích vì sao xác định duy nhất:...

Hoạt động khám phá 2 trang 26 Toán 11 Tập 1: Xét hai hàm số y = x², y = 2x và đồ thị của chúng trong Hình 2. Đối với mỗi trường hợp nêu mối liên hệ của giá trị hàm số tại 1 và – 1, 2 và – 2. Nhận xét về tính đối xứng của mỗi đồ thị hàm số....

Thực hành 1 trang 27 Toán 11 Tập 1: Chứng minh rằng hàm số y = sinx và hàm số y = cotx là các hàm số lẻ....

Hoạt động khám phá 3 trang 27 Toán 11 Tập 1: Hãy chỉ ra một số thực T sao cho sin(x + T) = sinx với mọi x ∈ℝ....

Thực hành 2 trang 27 Toán 11 Tập 1: Xét tính tuần hoàn của hàm số y = cosx và hàm số y = cotx....

Hoạt động khám phá 4 trang 28 Toán 11 Tập 1: Hoàn thành bảng giá trị sau đây và xác định các điểm tương ứng trên mặt phẳng tọa độ....

Hoạt động khám phá 5 trang 28 Toán 11 Tập 1: Hoàn thành bảng giá trị sau đây và xác định các điểm tương ứng trên mặt phẳng tọa độ....

Thực hành 3 trang 30 Toán 11 Tập 1: Cho hàm số y = cos x với x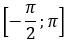 $\in$ ...

Vận dụng 1 trang 30 Toán 11 Tập 1: Li độ s(cm) của một con lắc đồng hồ theo thời gian t(giây) được cho bởi hàm số s = 2cos $π$ t. Dựa vào đồ thị của hàm số côsin, hãy xác định ở các thời điểm t nào trong 3 giây đầu thì con lắc có li độ lớn nhất....

Hoạt động khám phá 6 trang 30 Toán 11 Tập 1: Hoàn thành bảng giá trị sau đây và xác định các điểm tương ứng trên mặt phẳng tọa độ...

Hoạt động khám phá 7 trang 31 Toán 11 Tập 1: Hoàn thành bảng giá trị sau đây và xác định các điểm tương ứng trên mặt phẳng tọa độ....

Thực hành 4 trang 32 Toán 11 Tập 1: Có bao nhiêu giá trị x trên đoạn [–2π; 2π] thỏa mãn điều kiện tanx = 2?...

Vận dụng 2 trang 32 Toán 11 Tập 1: Trong địa lí, phép chiếu hình trụ được sử dụng để vẽ một bản đồ phẳng như trong Hình 10. Trên bản đồ phẳng lấy đường xích đạo làm trục hoàng và kinh tuyến 0⁰làm trục tung. Khi đó tung độ của một điểm có vĩ độ $φ^{o}$ (-90 < $φ$ < 90) được cho bởi hàm số y = 20tan $(\frac{π}{180} φ)$ (cm). Sử dụng đồ thị hàm số tang, hãy cho biết những điểm ở vĩ độ nào nằm cách xích đạo 20 cm trên bản đồ...

Bài 1 trang 32 Toán 11 Tập 1: Các hàm số dưới đây có là hàm số chẵn hay hàm số lẻ không?...

Bài 2 trang 32 Toán 11 Tập 1: Tìm tập xác định của các hàm số sau:...

Bài 3 trang 33 Toán 11 Tập 1: Tìm tập giá trị của hàm số y = 2cosx + 1....

Bài 4 trang 33 Toán 11 Tập 1: Dựa vào đồ thị hàm số y = sinx, xác định các giá trị x ∈ [– π; π] thỏa mãn sinx = $\frac{1}{2}$ ....

Bài 5 trang 33 Toán 11 Tập 1: Khi đu quay hoạt động, vận tốc theo phương ngang của một cabin M phụ thuộc vào góc lượng giác α = (Ox, OM) theo hàm số v_x = 0,3sin α (m/s) (Hình 11)....

Bài 6 trang 33 Toán 11 Tập 1: Khoảng cách từ tâm một guồng nước đến mặt nước và bán kính của guồng đều bằng 3m. Xét gàu G của guồng. Ban đầu gàu G nằm ở vị trí A (Hình 12)....

Bài 7 trang 33 Toán 11 Tập 1: Trong Hình 13, một chiếc máy bay A bay ở độ cao 500m theo một đường thẳng đi ngang qua phía trên trạm quan sát T ở mặt đất. Hình chiếu vuông góc của A lên mặt đất là H, α là góc lượng giác (Tx, TA) (0 < α < π)....

Xem thêm các bài giải SGK Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Các công thức lượng giác

Bài 4: Hàm số lượng giác và đồ thị

Bài 5: Phương trình lượng giác

Bài tập cuối chương 1

Bài 1: Dãy số

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Chứng minh rằng biểu thức sau luôn luôn dương với mọi x, y: B = x^2 - 2x + y^2 + 4y + 6

Chứng minh rằng biểu thức sau luôn luôn dương với mọi x, y: B = x^2 - 2x + y^2 + 4y + 6 Lữ Ngọc My My

55

Toán Tổng hợp kiến thức

3/(1^2.2^2 ) + 5/(2^2.3^2 ) + 7/(3^2.4^2 ) + ... + 19/(9^2.10^2). Chứng minh nhỏ hơn 1

3/(1^2.2^2 ) + 5/(2^2.3^2 ) + 7/(3^2.4^2 ) + ... + 19/(9^2.10^2). Chứng minh nhỏ hơn 1 Lữ Ngọc My My

52

Toán Tổng hợp kiến thức

Tính tổng: 1/4 + 1/12 + 1/24 + 1/40 + 1/60 + 1/84

Tính tổng: 1/4 + 1/12 + 1/24 + 1/40 + 1/60 + 1/84 Lữ Ngọc My My

42

Toán Tổng hợp kiến thức

Tìm x; y nguyên 2xy + 2x - y = 8

Tìm x; y nguyên 2xy + 2x - y = 8 Lữ Ngọc My My

43

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.