Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài 3: Các công thức lượng giác chi tiết sách Toán 11 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 3: Các công thức lượng giác

Giải Toán 11 trang 20 Tập 1

Hoạt động khởi động trang 20 Toán 11 Tập 1: Trong kiến trúc, các vòm cổng bằng đá thường có hình nửa đường tròn để có thể chịu lực tốt. Trong hình bên, vòm cổng được ghép bởi sáu phiến đá hai bên tạo thành các cung AB, BC, CD, EF, FG, GH bằng nhau và một phiến đá chốt ở đỉnh. Nếu biết chiều rộng cổng và khoảng cách từ điểm B đến đường kính AH, làm thế nào để tính được khoảng cách từ điểm C đến AH?

Lời giải:

Đặt chiều rộng cổng AH = d.

⇒ OA = OB = $\frac{1}{2}$d.

Xét tam giác OBB’ vuông tại B’, có:

$\sin \widehat{BOB\text{'}}=\frac{BB\text{'}}{OB}=\frac{27}{\frac{d}{2}}=\frac{54}{d}$.

Vì  nên sđ = 2.sđ $\Rightarrow \widehat{AOC}=2\widehat{BOB\text{'}}$

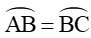
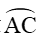
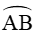
Xét tam giác OCC’ vuông tại C’, có:

Sau bài học này ta sẽ giải quyết tiếp được bài toán như sau:

Vậy khoảng cách này từ điểm C đến AH là $\frac{108}{d}\sqrt{1-{\left(\frac{54}{d}\right)}^2}$.

Giải Toán 11 trang 21 Tập 1

1. Công thức cộng

Hoạt động khám phá 1 trang 21 Toán 11 Tập 1: Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ $\overrightarrow{OM}$ và $\overrightarrow{ON}$ sau đây:

Hãy suy ra công thức tính cos(α – β) theo các giá trị lượng giác của α và β. Từ đó, hãy suy ra công thức cos(α + β) bằng cách thay β bằng – β.

Lời giải:

Ta có: cos(α – β) = x_M.x_N + y_M.y_N = cosα.cosβ + sinα.sinβ.

Ta có: cos(α + β) = cos(α – (– β)) = cosα.cos(–β) + sinα.sin(–β) = cosα.cosβ – sinα.sinβ.

Thực hành 1 trang 21 Toán 11 Tập 1: Tính sin$\frac{\pi }{12}$ và tan$\frac{\pi }{12}$.

Lời giải:

Ở ví dụ 1 ta có: cos$\frac{\pi }{12}=\frac{\sqrt{6}+\sqrt{2}}{4}$

Suy ra tan.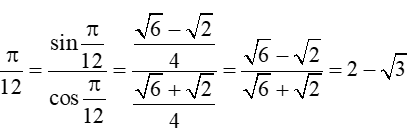

2. Công thức góc nhân đôi

Hoạt động khám phá 2 trang 21 Toán 11 Tập 1: Hãy áp dụng công thức cộng cho trường hợp β = α và tính các giá trị lượng giác của góc 2α.

Lời giải:

Ta có:

cos2α = cos(α + α) = cosα.cosα – sinα.sinα

= cos²α – sin²α = cos²α + sin²α – 2sin²α

= 1 – 2sin²α = 2cos²α – 1.

sin2α = sin(α + α) = sinα.cosα + cosα.sinα = 2.sinα.cosα .

.

Giải Toán 11 trang 22 Tập 1

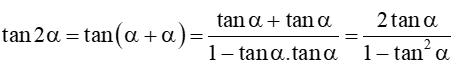
Thực hành 2 trang 22 Toán 11 Tập 1: Tính cos$\frac{\pi }{8}$ và tan$\frac{\pi }{8}$.

Lời giải:

+) Ta có:

3. Công thức biến đổi tích thành tổng

Hoạt động khám phá 3 trang 22 Toán 11 Tập 1: Từ công thức cộng, hãy tính tổng và hiệu của:

a) cos(α – β) và cos(α + β) ;

b) sin(α – β) và sin(α + β) .

Lời giải:

a) Ta có: cos(α – β) = cosα.cosβ + sinα.sinβ; cos(α + β)

= cosα.cosβ – sinα.sinβ

Khi đó:

cos(α – β) + cos(α + β) = cosα.cosβ + sinα.sinβ + cosα.cosβ – sinα.sinβ

= 2cosα.cosβ.

cos(α – β) – cos(α + β) = cosα.cosβ + sinα.sinβ – cosα.cosβ + sinα.sinβ

= 2sinα.sinβ .

b) Ta có: sin(α – β) = sinα.cosβ + cosα.sinβ; sin(α + β)

= sinα.cosβ – cosα.sinβ

Khi đó:

sin(α – β) + sin(α + β) = sinα.cosβ + cosα.sinβ + sinα.cosβ – cosα.sinβ

= 2sinα.cosβ.

sin(α – β) – sin(α + β) = sinα.cosβ + cosα.sinβ – sinα.cosβ + cosα.sinβ

= 2cosα.sinβ.

Thực hành 3 trang 22 Toán 11 Tập 1: Tính giá trị của các biểu thức sin$\frac{\pi }{24}$cos$\frac{5\pi }{24}$ và sin$\frac{7\pi }{8}$sin$\frac{5\pi }{8}$.

Lời giải:

Ta có:

4. Công thức biến đổi tổng thành tích

Hoạt động khám phá 4 trang 22 Toán 11 Tập 1: Áp dụng công thức biến đổi tích thành tổng cho hai góc lượng giác $a=\frac{\alpha +\beta }{2}$ và $b=\frac{\alpha -\beta }{2}$ ta được các đẳng thức nào?

Lời giải:

Ta có:

Giải Toán 11 trang 23 Tập 1

Thực hành 4 trang 23 Toán 11 Tập 1: Tính cos$\frac{7\pi }{12}$ + cos$\frac{\pi }{12}$.

Lời giải:

Vận dụng trang 23 Toán 11 Tập 1: Trong bài toán khởi động, cho biết vòm cổng rộng 120 cm và khoảng cách từ B đến đường kính AH là 27 cm. Tính sin α và cos α, từ đó tính khoảng cách từ điểm C đến đường kính AH. Làm tròn kết quả đến hàng phần mười.

Lời giải:

Ta có: OA = OB = $\frac{120}{2}$= 60 cm.

Xét tam giác OBB’ vuông tại B’, có:

$\sin \widehat{BOB\text{'}}=\frac{BB\text{'}}{OB}=\frac{27}{60}=\frac{9}{20}$.

$\Rightarrow \text{cos}\widehat{BOB\text{'}}=\sqrt{1-{\left(\frac{9}{20}\right)}^2}=\frac{\sqrt{319}}{20}$

Vì  nên sđ = 2.sđ $\Rightarrow \widehat{AOC}=2\widehat{BOB\text{'}}$

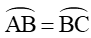
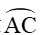
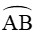
Xét tam giác OCC’ vuông tại C’, có:

Sau bài học này ta sẽ giải quyết tiếp được bài toán như sau:

Vậy khoảng cách này từ điểm C đến AH là $60.\frac{9\sqrt{319}}{200}\approx$48,2 (cm).

Bài tập

Bài 1 trang 23 Toán 11 Tập 1: Không dùng máy tính cầm tay, tính các giá trị lượng giác của các góc:

a) $\frac{5\pi }{12}$;

b) – 555°.

Lời giải:

a) Ta có:

b) Ta có:

– 555° = $\frac{\pi .\left(-555°\right)}{180°}=-\frac{37\pi }{12}=-\left(3\pi +\frac{\pi }{12}\right)$ rad.

Khi đó:

Bài 2 trang 23 Toán 11 Tập 1: Tính $\sin \left(\alpha +\frac{\pi }{6}\right),\text{cos}\left(\frac{\pi }{4}-\alpha \right)$ biết sin$\alpha =-\frac{5}{13}$ và $\pi <\alpha <\frac{3\pi }{2}$.

Lời giải:

Ta có: cos$\alpha =-\sqrt{1-{\left(-\frac{5}{13}\right)}^2}=-\frac{12}{13}$ (vì $\pi <\alpha <\frac{3\pi }{2}$).

Ta lại có:

Giải Toán 11 trang 24 Tập 1

Bài 3 trang 24 Toán 11 Tập 1: Tính các giá trị lượng giác của góc 2α, biết:

a) sin$\alpha$ = $\frac{\sqrt{3}}{3}$ và $0<\alpha <\frac{\pi }{2}$;

b) sin$\frac{\alpha }{2}=\frac{3}{4}$ và $\pi <\alpha <2\pi$.

Lời giải:

a) Ta có: 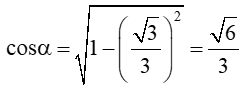 (vì $0<\alpha <\frac{\pi }{2}$).

Khi đó:

b) Ta có: 

Khi đó:

Bài 4 trang 24 Toán 11 Tập 1: Rút gọn các biểu thức sau:

a) $\sqrt{2}$sin$\left(\alpha +\frac{\pi }{4}\right)$ - cos$\alpha$;

b) (cos$\alpha$ + sin$\alpha$)² - sin2$\alpha$.

Lời giải:

a) $\sqrt{2}$sin$\left(\alpha +\frac{\pi }{4}\right)$ - cos$\alpha$

= sin$\alpha$ + cos$\alpha$ - cos$\alpha$

= sin$\alpha$.

b) (cos$\alpha$ + sin$\alpha$)² - sin2$\alpha$

= cos^2$\alpha$ + sin²$\alpha$ + 2sin$\alpha$cos$\alpha$ - 2sin$\alpha$cos$\alpha$

= 1

Bài 5 trang 24 Toán 11 Tập 1: Tính các giá trị lượng giác của góc α, biết:

a) $\text{cos}2\alpha =\frac{2}{5}$ và $-\frac{\pi }{2}<\alpha <0$;

b) $\sin 2\alpha =-\frac{4}{9}$ và $\frac{\pi }{2}<\alpha <\frac{3\pi }{4}$.

Lời giải:

a) Ta có: $\text{cos}2\alpha =2{\text{cos}}^2\alpha -1=\frac{2}{5}$

$\iff {\text{cos}}^2\alpha =\frac{7}{10}$

$\iff \text{cos}\alpha =\frac{\sqrt{70}}{10}$ (vì $-\frac{\pi }{2}<\alpha <0$).

Mặt khác $\text{cos}2\alpha =1-2{\sin }^2\alpha =\frac{2}{5}$

$\iff {\sin }^2\alpha =\frac{3}{10}$

$\iff \sin \alpha =-\frac{\sqrt{30}}{100}$ (vì $-\frac{\pi }{2}<\alpha <0$).

Khi đó:

b) $\sin 2\alpha =-\frac{4}{9}$ và $\frac{\pi }{2}<\alpha <\frac{3\pi }{4}$.

Ta có $\frac{\pi }{2}<\alpha <\frac{3\pi }{4}\iff \pi <2\alpha <\frac{3\pi }{2}$

Ta có: $\text{cos}2\alpha =2{\text{cos}}^2\alpha -1=-\frac{\sqrt{65}}{9}$

$\iff {\text{cos}}^2\alpha =\frac{9-\sqrt{65}}{18}$

$\iff \text{cos}\alpha =\sqrt{\frac{9-\sqrt{65}}{18}}$ (vì $\frac{\pi }{2}<\alpha <\frac{3\pi }{4}$).

Mặt khác $\text{cos}2\alpha =1-2{\sin }^2\alpha =-\frac{\sqrt{65}}{9}$

$\iff {\sin }^2\alpha =\frac{\sqrt{65}+1}{18}$

$\iff \sin \alpha =\frac{\sqrt{65}+1}{18}$ (vì $\frac{\pi }{2}<\alpha <\frac{3\pi }{4}$).

Khi đó:

Bài 6 trang 24 Toán 11 Tập 1: Chứng minh rằng tam giác ABC, ta có sinA = sinB.cosC + sinC.cosB.

Lời giải:

Xét tam giác ABC, có:

A + B + C = 180° ⇒ A = 180° – (B + C)

sinA = sin(180° – (B + C)) = sin(B + C) = sinB.cosC + sinC.cosB.

Bài 7 trang 24 Toán 11 Tập 1: Trong Hình 3, tam giác ABC vuông tại B và có hai cạnh góc vuông là AB = 4, BC = 3. Vẽ điểm D nằm trên tia đối của tia CB thỏa mãn $\widehat{CAD}=30°$. Tính tan$\widehat{BAD}$, từ đó tính độ dài cạnh CD.

Lời giải:

Xét tam giác ABC vuông tại B có:

tan$\widehat{BAC}=\frac{3}{4}$.

Ta lại có: $\widehat{BAD}=\widehat{BAC}+\widehat{CAD}$

Xét tam giác ABD vuông tại B có:

$\tan \widehat{BAD}=\frac{BD}{AB}\Rightarrow BD=\tan \widehat{BAD}.AB=2,34.4\approx 9,36$.

⇒ CD = BD – BC ≈ 9,36 – 3 = 6,36.

Bài 8 trang 24 Toán 11 Tập 1: Trong Hình 4, pít – tông M của động cơ chuyển động tịnh tiến qua lại dọc theo xi lanh làm quay trục khuỷu IA. Ban đầu I, A, M thẳng hàng. Cho α là góc quay của trục khuỷu, O là vị trí của pít – tông khi $\alpha =\frac{\pi }{2}$ và H là hình chiếu của A lên Ix. Trục khuỷu IA rất ngắn so với độ dài thanh truyền AM nên có thể xem như độ dài MH không đổi và gần bằng MA.

a) Biết IA = 8cm, viết công thức tính tọa độ x_M của điểm M trên trục Ox theo α.

b) Ban đầu α = 0. Sau 1 phút chuyển động, x_M = – 3cm. Xác định x_M sau 2 phút chuyển động. Làm tròn kết quả đến hàng phần mười.

Lời giải:

Tại $\alpha =\frac{\pi }{2}$ thì H trùng I, M trùng O nên MH = OI do đó OM = IH.

Xét tam giác AHI vuông tại H có: IH = cosα.IA = 8cosα.

Bài 9 trang 24 Toán 11 Tập 1: Trong Hình 5, ba điểm M, N, P nằm ở đầu các cánh quạt của tua bin gió. Biết các cánh quạt dài 31m, độ cao của điểm M so với mặt đất là 30m, góc giữa các cánh quạt là $\frac{2\pi }{3}$ và số đo góc (OA, OM) là α.

a) Tính sinα và cosα.

b) Tính sin của các góc lượng giác (OA, ON) và (OA, OP) từ đó tính chiều cao của các điểm N và P so với mặt đất (theo đơn vị mét). Làm tròn kết quả đến hàng phần trăm.

Lời giải:

a) Tính sinα và cosα

Từ điểm M kẻ MH vuông góc với Ox, MK vuông góc với Oy.

Ta có: MH = 60 – 30 = 30 m.

Khi đó hoành độ điểm M là 30.

Mặt khác hoành độ điểm M là: x_M = 31.cosα.

⇒ cosα = $\frac{30}{31}$

⇒ $\sin \alpha =-\sqrt{1-{\left(\frac{30}{31}\right)}^2}=-\frac{\sqrt{61}}{31}$.

b) Vì các cánh quạt tạo thành 3 góc bằng nhau nên $\widehat{MOP}=\widehat{NOP}=\widehat{MON}=120°$

Vì vậy chiều cao của điểm P so với mặt đất khoảng: 31.sinα + 60 = 89,76 m.

Ta có: $\text{cos}\widehat{AOP}\approx \sqrt{1-0,{96}^2}=0,28$.

Ta có: $\widehat{AON}=\widehat{AOP}+\widehat{PON}$

Vì vậy chiều cao của điểm N so với mặt đất khoảng: 31.sinα + 60 = 89,76 m.

Video bài giảng Toán 11 Bài 3: Các công thức lượng giác - Chân trời sáng tạo

Xem thêm các bài giải SGK Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Giá trị lượng giác của một góc lượng giác

Bài 3: Các công thức lượng giác

Bài 4: Hàm số lượng giác và đồ thị

Bài 5: Phương trình lượng giác

Bài tập cuối chương 1

Lý thuyết Các công thức lượng giác

1. Công thức cộng

$\begin{array}{l}\sin \left(a+b\right)=\sin a\cos b+\cos asinb\\ sin\left(a-b\right)=\sin a\cos b-\cos asinb\\ \cos \left(a+b\right)=\cos a\cos b-\sin asinb\\ \cos \left(a-b\right)=\cos a\cos b+\sin asinb\\ \tan \left(a+b\right)=\frac{\tan a+\tan b}{1-\tan a\tan b}\\ \tan \left(a-b\right)=\frac{\tan a-\tan b}{1+\tan a\tan b}\end{array}$

2. Công thức nhân đôi

$\begin{array}{l}\sin 2a=2\sin a\cos a\\ \cos 2a={\cos }^{2}a-{\sin }^{2}a=2{\cos }^{2}a-1=1-2{\sin }^{2}a\\ \tan 2a=\frac{2\tan a}{1-{\tan }^{2}a}\end{array}$

Suy ra, công thức hạ bậc:

 ${\sin }^{2}a=\frac{1-\cos 2a}{2},{\cos }^{2}a=\frac{1+\cos 2a}{2}$

3. Công thức biến đổi tích thành tổng

$\begin{array}{l}\cos a\cos b=\frac{1}{2}\left[\cos \left(a+b\right)+\cos \left(a-b\right)\right]\\ \sin a\sin b=\frac{1}{2}\left[\cos \left(a-b\right)-\cos \left(a+b\right)\right]\\ \sin a\cos b=\frac{1}{2}\left[\sin \left(a+b\right)+\sin \left(a-b\right)\right]\end{array}$

4. Công thức biến đổi tổng thành tích

$\begin{array}{l}\cos a+\cos b=2\cos \frac{a+b}{2}\cos \frac{a-b}{2}\\ \cos a-\cos b=-2\sin \frac{a+b}{2}\sin \frac{a-b}{2}\\ \sin a+\sin b=2\sin \frac{a+b}{2}\cos \frac{a-b}{2}\\ \sin a-\sin b=2\cos \frac{a+b}{2}\sin \frac{a-b}{2}\end{array}$