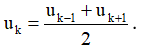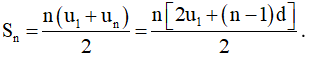Với giải Bài 2 trang 65 SBT Toán lớp 11 Chân trời sáng tạo chi tiết trong Bài tập cuối chương 2 trang 64 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:
Giải SBT Toán 11 Bài tập cuối chương 2 trang 64
Bài 2 trang 65 SBT Toán 11 Tập 1: Một tam giác vuông có chu vi bằng 3 và độ dài các cạnh lập thành cấp số cộng. Tính độ dài các cạnh của tam giác đó.
Lời giải:
Gọi d là công sai của cấp số cộng và các cạnh có độ dài lần lượt là: a ‒ d, a, a + d với 0 < d < a.
Vì tam giác có chu vi bằng 3 nên a ‒ d + a + a + d = 3a = 3, suy ra a = 1.
Vì đây là tam giác vuông nên cạnh lớn nhất là cạnh huyền, theo định lí Pythagore, ta có: (1 + d)2 = (1 ‒ d)2 + 12
Suy ra 1 + 2d + d2 = 1 – 2d + d2 + 1
Do đó 4d = 1
Suy ra
Khi đó và
Vậy ba cạnh của tam giác có độ dài là
Công thức Cấp số cộng
- Công thức tính tính công sai: d = un+1 – un với n ∈ N*.
- Công thức tìm số hạng tổng quát: un = u1 + (n – 1)d với n ∈ N*, n ≥ 2.
- Tính chất của 3 số hạng uk-1, uk, uk+1 (k ≥ 2) liên tiếp của cấp số cộng: 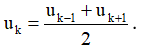
- Tổng n số hạng đầu tiên của cấp số cộng: 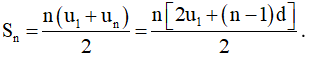
Xem thêm lời bài sách bài tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Câu 1 trang 64 SBT Toán 11 Tập 1: Cho dãy số (un), biết . Trong các khẳng định sau, khẳng định nào đúng?...
Câu 2 trang 64 SBT Toán 11 Tập 1: Trong các dãy số (un) cho bởi số hạng tổng quát un sau, dãy số nào bị chặn?....
Câu 3 trang 64 SBT Toán 11 Tập 1: Trong các dãy số (un) cho bởi số hạng tổng quát un sau, dãy số nào là dãy số tăng?...
Câu 4 trang 64 SBT Toán 11 Tập 1: Cho cấp số cộng (un), biết u1 = 3 và u2 = ‒1. Số hạng thứ ba của cấp số cộng đó là...
Câu 5 trang 64 SBT Toán 11 Tập 1: Cấp số cộng (un) có số hạng đầu u1 = 3, công sai d = 5. Số hạng thứ tư của cấp số cộng đó là....
Câu 6 trang 64 SBT Toán 11 Tập 1: Cho cấp số cộng (un) có u4 = ‒12, u14 = 18. Tổng của 16 số hạng đầu tiên của cấp số cộng đó là...
Câu 7 trang 64 SBT Toán 11 Tập 1: Cho cấp số cộng: ‒2; ‒5; ‒8; ‒11; ‒14. Công sai d và tổng 20 số hạng đầu tiên của cấp số cộng đó lần lượt là...
Câu 8 trang 64 SBT Toán 11 Tập 1: Một cấp số nhân có sáu số hạng, số hạng đầu là 2 và số hạng thứ sáu bằng 486. Gọi q là công bội của cấp số nhân đó. Giá trị của q là....
Câu 9 trang 64 SBT Toán 11 Tập 1: Một cấp số nhân có bốn số hạng, số hạng đầu là 3 và số hạng thứ tư là 192. Gọi S là tổng các số hạng của cấp số nhân đó. Giá trị của S là...
Câu 10 trang 64 SBT Toán 11 Tập 1: Trong các dãy số (un) được cho bởi số hạng tổng quát un sau, dãy số nào là cấp số nhân?...
Bài 1 trang 65 SBT Toán 11 Tập 1: Xét tính tăng, giảm và bị chặn của dãy số (un), biết...
Bài 2 trang 65 SBT Toán 11 Tập 1: Một tam giác vuông có chu vi bằng 3 và độ dài các cạnh lập thành cấp số cộng. Tính độ dài các cạnh của tam giác đó....
Bài 3 trang 65 SBT Toán 11 Tập 1: Chu vi của một đa giác là 213 cm, số đo các cạnh của nó lập thành cấp số cộng với công sai d = 7 cm và cạnh lớn nhất bằng 53 cm. Tính số cạnh của đa giác đó...
Bài 4 trang 65 SBT Toán 11 Tập 1: Cho a, b, c theo thứ tự lập thành cấp số cộng. Chứng minh: a2 ‒ c2 = 2ab ‒ 2bc...
Bài 5 trang 65 SBT Toán 11 Tập 1: Xác định số hạng đầu và công bội của cấp số nhân (un) có ...
Bài 6 trang 65 SBT Toán 11 Tập 1: Cho cấp số nhân (un), biết . Tìm u9....
Bài 7 trang 65 SBT Toán 11 Tập 1: Cho cấp số nhân: . Tính giá trị của a....
Bài 8 trang 65 SBT Toán 11 Tập 1: Một cấp số nhân có số hạng đầu u1 = 3, công bội q = 2. Biết Sn = 765. Tìm n....
Bài 9 trang 65 SBT Toán 11 Tập 1: Một tháp 10 tầng có diện tích sàn của tầng dưới cùng là 6 144 m2. Tính diện tích mặt sàn tầng trên cùng, biết rằng diện tích mặt sàn mỗi tầng bằng nửa diện tích mặt sàn tầng ngay bên dưới....
Bài 10 trang 65 SBT Toán 11 Tập 1: Một khay nước có nhiệt độ 20°C được đặt vào ngăn đá của tủ lạnh. Cho biết sau mỗi giờ, nhiệt độ của nước giảm đi 25%. Tính nhiệt độ khay nước đó sau 4 giờ....
Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Cấp số nhân
Bài tập cuối chương 2
Bài 1: Giới hạn của dãy số
Bài 2: Giới hạn của hàm số
Bài 3: Hàm số liên tục
Bài tập cuối chương 3