Sách bài tập Toán 11 Bài 2 (Chân trời sáng tạo): Giới hạn của hàm số

Admin Vietjack Ngày: 25-09-2024 Lớp 11

2.3 K

Với giải sách bài tập Toán 11 Bài 2: Giới hạn của hàm số sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài 2: Giới hạn của hàm số

Giải SBT Toán 11 trang 84

Bài 1 trang 84 SBT Toán 11 Tập 1: Sử dụng định nghĩa, tìm các giới hạn sau:

a) $\lim_{x \to - 1} (x^{3} - 3 x);$

b) $\lim_{x \to 2} \sqrt{2 x + 5};$

c) $\lim_{x \to + \infty} \frac{4 - x}{2 x + 1} .$

Lời giải:

a) Giả sử (x_n) là dãy số bất kì thỏa mãn x_n ≠ –1 với mọi n và limx_n = ‒1.

Ta có: $\lim (x_{n}^{3} - 3 x_{n}) = {({limx}_{n})}^{3} - 3 \lim x_{n} = {(- 1)}^{3} - 3 \cdot (- 1) = 2.$

Vậy $\lim_{x \to - 1} (x^{3} - 3 x) = 2.$

b) Giả sử (x_n) là dãy số bất kì thỏa mãn $x_{n} \geq - \frac{5}{2}$ , x_n ≠ 2 với mọi n và limx_n = 2.

Ta có:

$\lim \sqrt{2 x_{n} + 5} = \sqrt{\lim 2 x_{n} + \lim 5} = \sqrt{2 \lim x_{n} + \lim 5}$

$= \sqrt{2 \cdot 2 + 5} = \sqrt{9} = 3.$

Vậy $\lim_{x \to 2} \sqrt{2 x + 5} = 3.$

c) Giả sử (x_n) là dãy số bất kì thỏa mãn limx_n = +∞.

Ta có: $\lim \frac{4 - x_{n}}{2 x_{n} + 1}$ = $\frac{\lim \frac{4}{x_{n}} - \lim 1}{\lim 2 + \lim \frac{1}{x_{n}}}$ = $\frac{0 - 1}{2 + 0} = - \frac{1}{2} .$

Vậy $\lim_{x \to + \infty} \frac{4 - x}{2 x + 1} = - \frac{1}{2} .$

Bài 2 trang 84 SBT Toán 11 Tập 1: Tìm các giới hạn sau:

a) $\lim_{x \to - 3} (8 + 3 x - x^{2});$

b) $\lim_{x \to 2} [(5 x - 1) (2 - 4 x)];$

c) $\lim_{x \to - 2} \frac{x^{2} - x}{{(2 x + 1)}^{2}};$

d) $\lim_{x \to - 1} \sqrt{10 - 2 x^{2}} .$

Lời giải:

a) $\lim_{x \to - 3} (8 + 3 x - x^{2}) = 8 + 3 \lim_{x \to - 3} x - \lim_{x \to - 3} x^{2}$

$= 8 + 3 \cdot (- 3) - {(- 3)}^{2} = - 10.$

b) $\lim_{x \to 2} [(5 x - 1) (2 - 4 x)] = \lim_{x \to 2} (5 x - 1) \cdot \lim_{x \to 2} (2 - 4 x)$

$= (5 \lim_{x \to 2} x - 1) \cdot (2 - 4 \lim_{x \to 2} x)$

= (5.2 ‒ 1)(2 ‒ 4.2) = ‒54.

c) $\lim_{x \to - 2} \frac{x^{2} - x}{{(2 x + 1)}^{2}} = \frac{\lim_{x \to - 2} (x^{2} - x)}{\lim_{x \to - 2} (4 x^{2} + 4 x + 1)}$ $= \frac{\lim_{x \to - 2} x^{2} - \lim_{x \to - 2} x}{4 \lim_{x \to - 2} x^{2} + 4 \lim_{x \to - 2} x + 1}$

$= \frac{{(- 2)}^{2} - (- 2)}{4 \cdot {(- 2)}^{2} + 4 \cdot (- 2) + 1} = \frac{6}{9} = \frac{2}{3} .$

d) $\lim_{x \to - 1} \sqrt{10 - 2 x^{2}} = \sqrt{\lim_{x \to - 1} (10 - 2 x^{2})} = \sqrt{10 - \lim_{x \to - 1} 2 x^{2}}$

$= \sqrt{10 - 2 \lim_{x \to - 1} x^{2}} = \sqrt{10 - 2. {(- 1)}^{2}} = \sqrt{8} = 2 \sqrt{2} .$

Bài 3 trang 84 SBT Toán 11 Tập 1: Tìm các giới hạn sau:

a) $\lim_{x \to - 2} \frac{x^{2} - 4}{x + 2};$

b) $\lim_{x \to 1} \frac{x^{3} - 1}{1 - x};$

c) $\lim_{x \to 3} \frac{x^{2} - 4 x + 3}{x - 3};$

d) $\lim_{x \to - 2} \frac{2 - \sqrt{x + 6}}{x + 2};$

e) $\lim_{x \to 0} \frac{x}{\sqrt{x + 1} - 1};$

g) $\lim_{x \to 2} \frac{x^{2} - 4 x + 4}{x^{2} - 4} .$

Lời giải:

a) $\lim_{x \to - 2} \frac{x^{2} - 4}{x + 2} = \lim_{x \to - 2} \frac{(x + 2) (x - 2)}{x + 2}$ $= \lim_{x \to - 2} (x - 2) = - 2 - 2 = - 4.$

b) $\lim_{x \to 1} \frac{x^{3} - 1}{1 - x} = \lim_{x \to 1} \frac{(x - 1) (x^{2} + x + 1)}{- (x - 1)}$

$= \lim_{x \to 1} [- (x^{2} + x + 1)] = - (\lim_{x \to 1} x^{2} + \lim_{x \to 1} x + 1) = - 3.$

c) $\lim_{x \to 3} \frac{x^{2} - 4 x + 3}{x - 3} = \lim_{x \to 3} \frac{(x - 1) (x - 3)}{x - 3}$ $= \lim_{x \to 3} (x - 1) = 3 - 1 = 2$

d) $lim_{x \to - 2} \frac{2 - \sqrt{x + 6}}{x + 2} = lim_{x \to - 2} \frac{(2 - \sqrt{x + 6}) (2 + \sqrt{x + 6})}{(x + 2) (2 + \sqrt{x + 6})}$

$= lim_{x \to - 2} \frac{4 - (x + 6)}{(x + 2) (2 + \sqrt{x + 6})} = lim_{x \to - 2} \frac{- (x + 2)}{(x + 2) (2 + \sqrt{x + 6})}$

$= lim_{x \to - 2} \frac{- 1}{2 + \sqrt{x + 6}} = \frac{- 1}{2 + \sqrt{- 2 + 6}} = - \frac{1}{4} .$

e) $lim_{x \to 0} \frac{x}{\sqrt{x + 1} - 1} = lim_{x \to 0} \frac{x (\sqrt{x + 1} + 1)}{(\sqrt{x + 1} - 1) (\sqrt{x + 1} + 1)}$

$= lim_{x \to 0} \frac{x (\sqrt{x + 1} + 1)}{(x + 1) - 1} = lim_{x \to 0} (\sqrt{x + 1} + 1) = 2.$

g) $\lim_{x \to 2} \frac{x^{2} - 4 x + 4}{x^{2} - 4} = \lim_{x \to 2} \frac{{(x - 2)}^{2}}{(x + 2) (x - 2)}$

$= \lim_{x \to 2} \frac{x - 2}{x + 2} = \frac{\lim_{x \to 2} (x - 2)}{\lim_{x \to 2} (x + 2)} = \frac{0}{4} = 0.$

Bài 4 trang 84 SBT Toán 11 Tập 1: Cho hai hàm số f(x) và g(x) có $\lim_{x \to 4} f (x) = 2$ và $\lim_{x \to 4} g (x) = - 3.$ Tìm các giới hạn:

a) $\lim_{x \to 4} [g (x) - 3 f (x)];$

b) $\lim_{x \to 4} \frac{2 f (x) \cdot g (x)}{{[f (x) + g (x)]}^{2}} .$

Lời giải:

a) $\lim_{x \to 4} [g (x) - 3 f (x)] = (- 3) - 3 \cdot 2 = - 9.$

b) $\lim_{x \to 4} \frac{2 f (x) \cdot g (x)}{{[f (x) + g (x)]}^{2}} = \frac{2 \cdot 2 \cdot (- 3)}{{[2 + (- 3)]}^{2}} = \frac{- 12}{1} = - 12.$

Bài 5 trang 84 SBT Toán 11 Tập 1: Cho hai hàm số f(x) và g(x) có $\lim_{x \to + \infty} f (x) = 3$ và $\lim_{x \to + \infty} [f (x) + 2 g (x)] = 7 .$

Tìm $\lim_{x \to + \infty} \frac{2 f (x) + g (x)}{2 f (x) - g (x)} .$

Lời giải:

Ta có $\lim_{x \to + \infty} [f (x) + 2 g (x)] = 7 .$

$\Rightarrow \lim_{x \to + \infty} f (x) + 2 \lim_{x \to + \infty} g (x) = 7$

$\Rightarrow 3 + 2 \lim_{x \to + \infty} g (x) = 7$

$\Rightarrow \lim_{x \to + \infty} g (x) = 2$

Suy ra $\lim_{x \to + \infty} \frac{2 f (x) + g (x)}{2 f (x) - g (x)} = \frac{2 \lim_{x \to + \infty} f (x) + \lim_{x \to + \infty} g (x)}{2 \lim_{x \to + \infty} f (x) - \lim_{x \to + \infty} g (x)}$ $= \frac{2 \cdot 3 + 2}{2 \cdot 3 - 2} = 2 .$

Bài 6 trang 84 SBT Toán 11 Tập 1: Cho hàm số $f (x) = \{\begin{cases} 3 x + 4, x \leq - 1 \\ 3 - 2 x^{2}, x > - 1 \end{cases} .$

Tìm các giới hạn $\lim_{x \to - 1^{+}} f (x), \lim_{x \to - 1^{-}} f (x)$ và $\lim_{x \to - 1} f (x) .$

Lời giải:

Ta có:

⦁ $\lim_{x \to - 1^{+}} f (x) = \lim_{x \to - 1^{+}} (3 - 2 x^{2}) = \lim_{x \to - 1^{+}} 3 - 2 \lim_{x \to - 1^{+}} x^{2}$

$= 3 - 2 \cdot {(- 1)}^{2} = 1.$

⦁ $\lim_{x \to - 1^{-}} f (x) = \lim_{x \to - 1^{-}} (3 x + 4) = 3 \lim_{x \to - 1^{-}} x + 4 = 3 \cdot (- 1) + 4 = 1 .$

⦁ Vì $\lim_{x \to - 1^{+}} f (x) = \lim_{x \to - 1^{-}} f (x) = 1$ nên $\lim_{x \to - 1} f (x) = 1 .$

Bài 7 trang 84 SBT Toán 11 Tập 1: Cho hàm số $f (x) = \{\begin{cases} 2 x + 1, x \leq 1 \\ \sqrt{x^{2} + a}, x > 1 . \end{cases}$

Tìm giá trị của tham số a sao cho tồn tại giới hạn $\lim_{x \to 1} f (x) .$

Lời giải:

Ta có: $\lim_{x \to 1^{-}} f (x) = \lim_{x \to 1^{-}} (2 x + 1) = 2 \lim_{x \to 1^{-}} x + 1 = 2 \cdot 1 + 1 = 3;$

$\lim_{x \to 1^{+}} f (x) = \lim_{x \to 1^{+}} \sqrt{x^{2} + a} = \sqrt{\lim_{x \to 1^{+}} (x^{2} + a)} = \sqrt{1 + a};$

Để tồn tại $\lim_{x \to 1} f (x)$ thì $\lim_{x \to 1^{-}} f (x) = \lim_{x \to 1^{+}} f (x)$

Tức là $\sqrt{1 + a} = 3,$ suy ra a = 8.

Giải SBT Toán 11 trang 85

Bài 8 trang 85 SBT Toán 11 Tập 1: Mỗi giới hạn sau có tồn tại không? Nếu có, hãy tìm giới hạn đó.

a) $\lim_{x \to 0} \frac{x^{2}}{|x|};$

b) $\lim_{x \to 2} \frac{x^{2} - 2 x}{|x - 2|} .$

Lời giải:

a) Ta có:

⦁ $\lim_{x \to 0^{-}} \frac{x^{2}}{|x|} = \lim_{x \to 0^{-}} \frac{x^{2}}{- x} = \lim_{x \to 0^{-}} \frac{x}{- 1} = \lim_{x \to 0^{-}} (- x) = 0;$

⦁ $\lim_{x \to 0^{+}} \frac{x^{2}}{|x|} = \lim_{x \to 0^{+}} \frac{x^{2}}{x} = \lim_{x \to 0^{+}} \frac{x}{1} = \lim_{x \to 0^{+}} x = 0.$

Do $\lim_{x \to 0^{-}} \frac{x^{2}}{|x|} = \lim_{x \to 0^{+}} \frac{x^{2}}{|x|} = 0$ nên tồn tại giới hạn $\lim_{x \to 0} \frac{x^{2}}{|x|}$ và $\lim_{x \to 0} \frac{x^{2}}{|x|} = 0.$

b) Ta có:

⦁ $\lim_{x \to 2^{+}} \frac{x^{2} - 2 x}{|x - 2|} = \lim_{x \to 2^{+}} \frac{x^{2} - 2 x}{x - 2}$ $= \lim_{x \to 2^{+}} \frac{x (x - 2)}{x - 2} = \lim_{x \to 2^{+}} x = 2.$

⦁ $\lim_{x \to 2^{-}} \frac{x^{2} - 2 x}{|x - 2|} = \lim_{x \to 2^{-}} \frac{x^{2} - 2 x}{2 - x}$ $= \lim_{x \to 2^{-}} \frac{x (x - 2)}{2 - x} \lim_{x \to 2^{-}} (- x) = - 2.$

Do $\lim_{x \to 2^{+}} \frac{x^{2} - 2 x}{|x - 2|} \neq \lim_{x \to 2^{-}} \frac{x^{2} - 2 x}{|x - 2|}$ nên không tồn tại giới hạn $\lim_{x \to 2} \frac{x^{2} - 2 x}{|x - 2|} .$

Bài 9 trang 85 SBT Toán 11 Tập 1: Tìm các giới hạn sau:

a) $\lim_{x \to + \infty} \frac{x}{x + 4};$

b) $\lim_{x \to - \infty} \frac{2 x^{2} + 1}{{(2 x + 1)}^{2}};$

c) $\lim_{x \to - \infty} \frac{3 x + 1}{\sqrt{x^{2} - 2 x}};$

d) $\lim_{x \to + \infty} (x - \sqrt{x^{2} + 2 x}) .$

Lời giải:

a) $\lim_{x \to + \infty} \frac{x}{x + 4} = \lim_{x \to + \infty} \frac{1}{1 + \frac{4}{x}} = \frac{1}{1 + 4 \cdot 0} = 1 .$

b) $\lim_{x \to - \infty} \frac{2 x^{2} + 1}{{(2 x + 1)}^{2}} = \lim_{x \to - \infty} \frac{2 + \frac{1}{x^{2}}}{{(2 + \frac{1}{x})}^{2}} = \frac{2 + 0}{{(2 + 0)}^{2}} = \frac{1}{2} .$

c) Với x < 0 thì $\sqrt{x^{2}} = |x| = - x,$ nên ta có:

$\lim_{x \to - \infty} \frac{3 x + 1}{\sqrt{x^{2} - 2 x}} = \lim_{x \to - \infty} \frac{x (3 + \frac{1}{x})}{- x \sqrt{1 - \frac{2}{x}}}$ $= \lim_{x \to - \infty} \frac{3 + \frac{1}{x}}{- \sqrt{1 - \frac{2}{x}}} = - \frac{3 + 0}{\sqrt{1 - 2 \cdot 0}} = - 3 .$

d) $\lim_{x \to + \infty} (x - \sqrt{x^{2} + 2 x}) = \lim_{x \to + \infty} \frac{(x - \sqrt{x^{2} + 2 x}) (x + \sqrt{x^{2} + 2 x})}{x + \sqrt{x^{2} + 2 x}}$

$= \lim_{x \to + \infty} \frac{x^{2} - (x^{2} + 2 x)}{x + \sqrt{x^{2} + 2 x}} = \lim_{x \to + \infty} \frac{- 2 x}{x + x \sqrt{1 + \frac{2}{x}}}$

$= \lim_{x \to + \infty} \frac{- 2}{1 + \sqrt{1 + \frac{2}{x}}} = \frac{- 2}{1 + 1} = - 1 .$

Bài 10 trang 85 SBT Toán 11 Tập 1: Tính các giới hạn sau:

a) $\lim_{x \to - \infty} (x^{3} + 2 x^{2} - 1);$

b) $\lim_{x \to + \infty} \frac{x^{3} + 2 x^{2}}{3 x^{2} + 1};$

c) $\lim_{x \to - \infty} \sqrt{x^{2} - 2 x + 3} .$

Lời giải:

a) $\lim_{x \to - \infty} (x^{3} + 2 x^{2} - 1) = \lim_{x \to - \infty} [x^{3} (1 + \frac{2}{x} - \frac{1}{x^{3}})]$

Ta có $\lim_{x \to - \infty} x^{3} = - \infty$ và $\lim_{x \to - \infty} (1 + \frac{2}{x} - \frac{1}{x^{3}}) = 1 + 0 - 0 = 1.$

Suy ra $\lim_{x \to - \infty} (x^{3} + 2 x^{2} - 1) = \lim_{x \to - \infty} [x^{3} (1 + \frac{2}{x} - \frac{1}{x^{3}})] = - \infty .$

b) $\lim_{x \to + \infty} \frac{x^{3} + 2 x^{2}}{3 x^{2} + 1} = \lim_{x \to + \infty} [x \cdot \frac{x^{2} + 2 x}{3 x^{2} + 1}]$

Ta có $\lim_{x \to + \infty} x = + \infty$ và $\lim_{x \to + \infty} \frac{x^{2} + 2 x}{3 x^{2} + 1} = \lim_{x \to + \infty} \frac{1 + \frac{2}{x}}{3 + \frac{1}{x^{2}}} = \frac{1}{3}$

Suy ra $\lim_{x \to + \infty} \frac{x^{3} + 2 x^{2}}{3 x^{2} + 1} = \lim_{x \to + \infty} [x \cdot \frac{x^{2} + 2 x}{3 x^{2} + 1}] = + \infty .$

c) $\lim_{x \to - \infty} \sqrt{x^{2} - 2 x + 3} = \lim_{x \to - \infty} \sqrt{x^{2} (1 - \frac{2}{x} + \frac{3}{x^{2}})}$

$= \lim_{x \to - \infty} (|x| \sqrt{1 - \frac{2}{x} + \frac{3}{x^{2}}})$

Ta có $\lim_{x \to - \infty} |x| = \lim_{x \to - \infty} (- x) = + \infty$ và $\lim_{x \to - \infty} \sqrt{1 - \frac{2}{x} + \frac{3}{x^{2}}} = 1$

Suy ra $\lim_{x \to - \infty} \sqrt{x^{2} - 2 x + 3} = \lim_{x \to - \infty} (|x| \sqrt{1 - \frac{2}{x} + \frac{3}{x^{2}}}) = + \infty .$

Bài 11 trang 85 SBT Toán 11 Tập 1: Tìm giá trị của các tham số a và b, biết rằng:

a) $\lim_{x \to 2} \frac{ax + b}{x - 2} = 5;$

b) $\lim_{x \to 1} \frac{a \sqrt{x} + b}{x - 1} = 3 .$

Lời giải:

a) Do $\lim_{x \to 2} (x - 2) = 2 - 2 = 0$ nên để tồn tại giới hạn hữu hạn $\lim_{x \to 2} \frac{ax + b}{x - 2} = 5,$ trước hết ta phải có $\lim_{x \to 2} (ax + b) = 0$ hay 2a + b = 0, suy ra b = ‒2a.

Khi đó, $\lim_{x \to 2} \frac{ax + b}{x - 2} = \lim_{x \to 2} \frac{ax - 2 a}{x - 2}$ $= \lim_{x \to 2} \frac{a (x - 2)}{x - 2} = \lim_{x \to 2} a = a$

Suy ra a = 5 và b = ‒10.

b) Do $\lim_{x \to 1} (x - 1) = 1 - 1 = 0$ nên để tồn tại giới hạn hữu hạn $\lim_{x \to 1} \frac{a \sqrt{x} + b}{x - 1} = 3,$ trước hết ta phải có $\lim_{x \to 1} (a \sqrt{x} + b) = 0$ hay a + b = 0, suy ra b = ‒a.

Khi đó, $\lim_{x \to 1} \frac{a \sqrt{x} + b}{x - 1} = \lim_{x \to 1} \frac{a \sqrt{x} - a}{x - 1}$ $= \lim_{x \to 1} \frac{a (\sqrt{x} - 1)}{x - 1} = \lim_{x \to 1} \frac{a (\sqrt{x} - 1) (\sqrt{x} + 1)}{(x - 1) (\sqrt{x} + 1)}$

$= lim_{x \to 1} \frac{a (x - 1)}{(x - 1) (\sqrt{x} + 1)} = lim_{x \to 1} \frac{a}{\sqrt{x} + 1} = \frac{a}{2} .$

Suy ra $\frac{a}{2} = 3$ hay a = 6, suy ra b = ‒6.

Bài 12 trang 85 SBT Toán 11 Tập 1: Trong mặt phẳng toạ độ Oxy, cho điểm M(t, t²), t > 0, nằm trên đường parabol y = x². Đường trung trực của đoạn thẳng OM cắt trục tung tại N. Điểm N dần đến điểm nào khi điểm M dần đến điểm O?

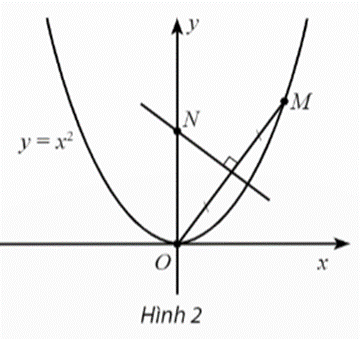
Trong mặt phẳng toạ độ Oxy cho điểm M(t, t^2) t > 0 nằm trên đường parabol y = x^2

Lời giải:

Trung điểm của đoạn thẳng OM là $I (\frac{t}{2}; \frac{t^{2}}{2})$

Đường trung trực của OM nhận $\vec{OM} = (t, t^{2})$ làm vectơ pháp tuyến và đi qua điểm $I (\frac{t}{2}; \frac{t^{2}}{2})$ nên có phương trình $d : t (x - \frac{t}{2}) + t^{2} (y - \frac{t^{2}}{2}) = 0$ .

Do đường trung trực của đoạn thẳng OM cắt trục tung tại N nên thay x = 0 vào phương trình của d, ta nhận được $y = \frac{1}{2} (1 + t^{2})$ .

Suy ra $N (0; \frac{1}{2} (1 + t^{2}))$

Điểm M dần đến điểm O khi t dần đến 0⁺. Ta có $\lim_{x \to 0^{+}} \frac{1}{2} (1 + t^{2}) = \frac{1}{2}$ .

Suy ra khi điểm M dần đến điểm O thì điểm N dần đến điểm $A (0; \frac{1}{2})$ .

Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Giới hạn của dãy số

Bài 2: Giới hạn của hàm số

Bài 3: Hàm số liên tục

Bài tập cuối chương 3

Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian

Bài 2: Hai đường thẳng song song

Lý thuyết Giới hạn của hàm số

1. Giới hạn hữu hạn của hàm số tại một điểm

Cho khoảng K chứa điểm $x_{0}$ và hàm số $y = f (x)$ xác định trên K hoặc trên $K ∖ {x_{0}}$ . Ta nói hàm số $y = f (x)$ có giới hạn hữu hạn là số L khi $x$ dần tới $x_{0}$ nếu với dãy số $(x_{n})$ bất kì, $x_{n} \in K ∖ {x_{0}}$ và $x_{n} \to x_{0}$ , ta có $f (x_{n}) \to L$

Kí hiệu $lim_{x \to x_{0}} f (x) = L$ hay $f (x) \to L$ , khi $x_{n} \to x_{0}$ .

2. Các phép toán về giới hạn hữu hạn của hàm số

a, Nếu $lim_{x \to x_{0}} f (x) = L$ và $lim_{x \to x_{0}} g (x) = M$ thì

$lim_{x \to x_{0}} [f (x) \pm g (x)] = L \pm M$

$lim_{x \to x_{0}} [f (x) . g (x)] = L . M$

$lim_{x \to x_{0}} [\frac{f (x)}{g (x)}] = \frac{L}{M} (M \neq 0)$

b, Nếu $f (x) \geq 0$ với mọi $x \in (a; b) ∖ {x_{0}}$ và $lim_{x \to x_{0}} f (x) = L$ thì $L \geq 0$ và $lim_{x \to x_{0}} \sqrt{f (x)} = \sqrt{L}$ .

* Nhận xét:

$\begin{array}{l} a, lim_{x \to x_{0}} x^{k} = {x_{0}}^{k}, k \in Z^{+} . \\ b, lim_{x \to x_{0}} [c . f (x)] = c . lim_{x \to x_{0}} f (x) \end{array}$

( $c \in R$ , nếu tồn tại $lim_{x \to x_{0}} f (x) \in R$ )

3. Giới hạn một phía

Cho hàm số $y = f (x)$ xác định trên khoảng $(x_{0}; b)$ .

Ta nói $y = f (x)$ có giới hạn bên phải là số L khi $x \to x_{0}$ nếu với dãy số $(x_{n})$ bất kì, $x_{0} < x_{n} < b$ và $x_{n} \to x_{0}$ ta có $f (x_{n}) \to L$ , kí hiệu $lim_{x \to {x_{0}}^{+}} f (x) = L$ .

Cho hàm số $y = f (x)$ xác định trên khoảng $(a; x_{0})$ .

Ta nói $y = f (x)$ có giới hạn bên phải là số L khi $x \to x_{0}$ nếu với dãy số $(x_{n})$ bất kì, $a < x_{n} < x_{0}$ và $x_{n} \to x_{0}$ ta có $f (x_{n}) \to L$ , kí hiệu $lim_{x \to {x_{0}}^{-}} f (x) = L$ .

*Chú ý:

$lim_{x \to x_{0}} f (x) = L \Leftrightarrow lim_{x \to {x_{0}}^{-}} f (x) = lim_{x \to {x_{0}}^{+}} f (x) = L$

$lim_{x \to {x_{0}}^{-}} f (x) \neq lim_{x \to {x_{0}}^{+}} f (x)$ thì không tồn tại $lim_{x \to x_{0}} f (x)$ .

Các phép toán về giới hạn hữu hạn của hàm số ở Mục 2 vẫn đúng khi ta thay $x \to x_{0}$ bằng $x \to {x_{0}}^{+}$ hoặc $x \to {x_{0}}^{-}$ .

4. Giới hạn hữu hạn của hàm số tại vô cực

Cho hàm số $y = f (x)$ xác định trên khoảng $(a; + \infty)$ . Ta nói hàm số $f (x)$ có giới hạn là số L khi $x \to + \infty$ nếu với dãy số $(x_{n})$ bất kì $x_{n} > a$ và $x_{n} \to + \infty$ ta có $f (x_{n}) \to L$ , kí hiệu $lim_{x \to + \infty} f (x) = L$ hay $f (x) \to L$ khi $x \to + \infty$ .

Cho hàm số $y = f (x)$ xác định trên khoảng $(- \infty; a)$ . Ta nói hàm số $f (x)$ có giới hạn là số L khi $x \to - \infty$ nếu với dãy số $(x_{n})$ bất kì $x_{n} < a$ và $x_{n} \to - \infty$ ta có $f (x_{n}) \to L$ , kí hiệu $lim_{x \to - \infty} f (x) = L$ hay $f (x) \to L$ khi $x \to - \infty$ .

* Nhận xét:

Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực.
Với c là hằng số, k là một số nguyên dương ta có:

$lim_{x \to \pm \infty} c = c,$ $lim_{x \to \pm \infty} (\frac{c}{x^{k}}) = 0$

5. Giới hạn vô cực của hàm số tại một điểm

- Cho hàm số $y = f (x)$ xác định trên khoảng $(x_{0}; b)$ .

Ta nói hàm số $f (x)$ có giới hạn bên phải là $+ \infty$ khi $x \to x_{0}$ về bên phải nếu với dãy số $(x_{n})$ bất kì thỏa mãn $x_{0} < x_{n} < b$ và $x_{n} \to x_{0}$ ta có $f (x_{n}) \to + \infty$ , kí hiệu $lim_{x \to {x_{0}}^{+}} f (x) = + \infty$

Ta nói hàm số $f (x)$ ó giới hạn bên phải là $- \infty$ khi $x \to x_{0}$ về bên trái nếu với dãy số $(x_{n})$ bất kì thỏa mãn $a < x_{n} < x_{0}$ và $x_{n} \to x_{0}$ ta có $f (x_{n}) \to + \infty$ , kí hiệu $lim_{x \to {x_{0}}^{-}} f (x) = + \infty$

Các giới hạn một bên $lim_{x \to {x_{0}}^{+}} f (x) = - \infty$ , $lim_{x \to {x_{0}}^{-}} f (x) = - \infty$ được định nghĩa tương tự.

* Chú ý:

$lim_{x \to + \infty} x^{k} = + \infty, k \in Z^{+} .$
$lim_{x \to - \infty} x^{k} = + \infty,$ k là số nguyên dương chẵn.
$lim_{x \to - \infty} x^{k} = - \infty,$ k là số nguyên dương lẻ.
$lim_{x \to a^{+}} \frac{1}{x - a} = + \infty, lim_{x \to a^{-}} \frac{1}{x - a} = - \infty (a \in R)$

Giới hạn vô cực

Nếu $lim_{x \to {x_{0}}^{+}} f (x) = L \neq 0$ và $lim_{x \to {x_{0}}^{+}} g (x) = + \infty$ hoặc $lim_{x \to {x_{0}}^{+}} g (x) = - \infty$ thì $lim_{x \to {x_{0}}^{+}} [f (x) . g (x)]$ được tính như sau: