Cho hình thoi ABCD có góc B tù. Kẻ BE vuông góc AD tại E

Cho hình thoi ABCD có góc B tù. Kẻ BE vuông góc AD tại E

Van Anh Ngày: 05-09-2023 Lớp 8

441

Với giải Bài 26 trang 99 SBT Toán lớp 8 Cánh diều chi tiết trong Bài 6: Hình thoi giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 6: Hình thoi

Bài 26 trang 99 SBT Toán 8 Tập 1: Cho hình thoi $A B C D$ có góc $B$ tù. Kẻ $B E$ vuông góc $A D$ tại $E$ , $B F$ vuông góc với $C D$ tại $F$ . Gọi $M, N$ lần lượt là giao điểm của $B E, B F$ với $A C$ . Chứng minh tứ giác $B M D N$ là hình thoi.

Lời giải:

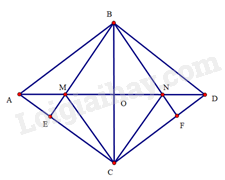
Sách bài tập Toán 8 Bài 6 (Cánh diều): Hình thoi (ảnh 1)

Gọi $O$ là giao điểm của $A C$ và $B D$

Do $A B C D$ là hình thoi nên $A C$ vuông góc với $B D$ tại trung điểm $O$ của $B D$ . Suy ra $A C$ là đường trung trực của $B D$ . Do đó $B M = D M, B N = D N$ .

Do $A B C D$ là hình thoi nên $B A = B C, \hat{B A E} = \hat{B C F}$ .

Suy ra $Δ A B E = Δ B C F$ (cạnh huyền – góc nhọn kề)

Do đó $\hat{A B E} = \hat{C B F}$ . Mà $\hat{A B D} = \hat{C B D}$ , suy ra $\hat{M B O} = \hat{N B O}$ .

$Δ M B O = Δ N B O$ (cạnh góc vuông – góc nhọn). suy ra $B M = B N$

Mà $B M = D M$ và $B N = D N$ , suy ra $B M = D M = B N = D N$ .

Tứ giác $B M D N$ có $B M = D M = B N = D N$ nên $B M D N$ là hình thoi.

Xem thêm lời giải sách bài tập Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài 26 trang 99 SBT Toán 8 Tập 1: Cho hình thoi $A B C D$ có góc $B$ tù. Kẻ $B E$ vuông góc $A D$ tại $E$ , $B F$ vuông góc với $C D$ tại $F$ . Gọi $M, N$ lần lượt là giao điểm của $B E, B F$ với $A C$ . Chứng minh tứ giác $B M D N$ là hình thoi......

Bài 27 trang 99 SBT Toán 8 Tập 1: Cho một hình thoi có độ dài hai đường chéo là $\frac{18}{5}$ m và $\frac{27}{10}$ m. Tính chu vi và diện tích của hình thoi đó....

Bài 28 trang 100 SBT Toán 8 Tập 1: Cho tam giác $A B C$ nhọn có các đường cao $B D, C E$ . Tia phân giác của các góc $A C E, A B D$ cắt nhau tại $O$ và cắt $A B, A C$ lần lượt tại $M, N$ . Tia $B N$ cắt $C E$ tại $K$ , tia $C M$ cắt $B D$ tại $H$ . Chứng minh:...

Bài 29 trang 100 SBT Toán 8 Tập 1: Cho góc $x O y$ khác góc bẹt. Dùng thước hai lề (thước có hai cạnh song song). Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh $O x$ của góc $x O y$ , vẽ đường thẳng $a$ theo cạnh kia của thước. đặt thước hai lề sao cho một cạnh của thước trùng với cạnh $O y$ của góc $x O y$ . Chứng minh tia $O M$ là tia phân giác của góc $x O y$ ....

Bài 30 trang 100 SBT Toán 8 Tập 1: Cho hình thoi $A B C D$ có $A B = 2$ cm, $\hat{A} = \frac{1}{2} \hat{B}$ . Các điểm $H, K$ thay đổi lần lượt trên cạnh $A D, C D$ sao cho $\hat{H B K} = 60^{\circ}$ .....

Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài 4: Hình bình hành

Bài 5: Hình chữ nhật

Bài 6: Hình thoi

Bài 7: Hình vuông

Bài tập cuối chương 5

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

162

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

135

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

112

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

108

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.