Với giải Bài 26 trang 62 SBT Toán lớp 8 Cánh diều chi tiết trong Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0) giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)

Bài 26 trang 62 SBT Toán 8 Tập 1: Một thiết bị tiệt khuẩn y tế bằng năng lượng mặt trời được mua với giá 60 triệu đồng, mỗi năm thiết bị tiệt khuẩn đó đều khấu hao $k$ (triệu đồng) với $0<k<60$. Gọi $y$ (triệu đồng) là giá của thiết bị tiệt khuẩn đó sau $x$ năm sử dụng.

a) Chứng tỏ rẳng $y$ là hàm số bậc nhất của $x$, tức là $y=ax+b\left(a\ne 0\right)$.

b) Trong Hình 10, tia $At$ là một phần của đường thẳng $y=ax+b$. Tìm $a,b$. Từ đó, cho biết sau 12 năm sử dụng thì giá của thiết bị tiệt khuẩn đó bằng bao nhiêu phần trăm so với giá mua ban đầu.

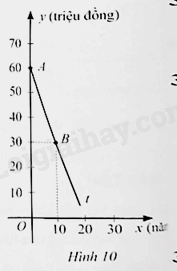
Lời giải:

a) Công thức biểu thị giá của thiết bị tiệt khuẩn đó sau $x$ năm sử dụng là: $y=60-kx$ hay $y=-kx+60$. Mà $k\ne 0$, suy ra $y$ là hàm số bậc nhất của $x$.

b) Từ câu a, ta có $b=60$. Do đường thẳng $y=ax+b$ đi qua điểm $B\left(10;30\right)$ nên $30=a.10+60$. Suy ra $a=-3$. Khi đó, đường thẳng cần tìm là: $y=-3x+60$.

Giá của thiết bị tiệt khuẩn đó sau 12 năm sử dụng là:

$-3.12+60=24$ (triệu đồng)

Tỉ số phần trăm giữa giá của thiết bị tiệt khuẩn đó sau 12 năm sử dụng và giá mua ban đầu là: $\frac{24.100}{60}\mathrm{\%}=40\mathrm{\%}$.

Vậy sau 12 năm sử dụng thì giá của thiết bị tiệt khuẩn đó bằng $40\mathrm{\%}$ so với giá mua ban đầu.