Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 8 Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0), được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0). Mời các bạn đón xem:
Bài tập Toán 8 Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)
A. Bài tập Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)
Bài 1: Chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song trong các đường thẳng sau: y = 3x + 1; y = 3x; y = −2x – 2.
Hướng dẫn giải
Cặp đường thẳng song song là: y = 3x + 1; y = 3x.
Cặp đường thẳng cắt nhau là: y = 3x + 1 và y = −2x – 2; y = 3x và y = −2x – 2.
Bài 2: Vẽ đồ thị của các hàm số y = 3x; y = −x − 2 trên cùng một mặt phẳng tọa độ?
Hướng dẫn giải
+ Với x = 1 thì y = 3, ta được điểm A(1; 3) thuộc đồ thị hàm số y = 3x.
Vẽ đồ thị hàm số y = 3x là đường thẳng đi qua gốc tọa độ và điểm A.
+ Với x = 0 thì y = −2, ta được điểm P(0; −2) thuộc đồ thị hàm số y = −x − 2.
Với y = 0 thì x = −2, ta được điểm Q(−2; 0) thuộc đồ thị hàm số y = −x − 2.
Vẽ đồ thị hàm số y = −x – 2 là đường thẳng đi qua hai điểm P và Q.
Bài 3: a) Xác định đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng −1 và đi qua điểm M(1; 2)?
b) Xác định đường thẳng y = ax + b (a ≠ 0) đi qua điểm M(1; 3) và song song với đường thẳng y = 2x?
Hướng dẫn giải
a) Vì đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng −1 nên đường thẳng có dạng y = - x + b
y = −x + b.
Vì đường thẳng y = −x + b đi qua điểm M(1; 2) nên ta có: 2 = −1 + b b = 3.
Vậy y = −x + 3.
b) Vì đường thẳng y = ax + b (a ≠ 0) song song với đường thẳng y = 2x nên đường thẳng có dạng: y = 2x + b.
Mà đường thẳng y = 2x + b đi qua điểm M(1; 3) nên 3 = 2.1 + b b = 1.
Vậy y = 2x +1.
Bài 4: Cho hai đường thẳng và Tung độ giao điểm của hai đường thẳng và là:
Đáp án : D
Xét phương trình hoành độ giao điểm của và :
Với thì
Vậy tung độ giao điểm của hai đường thẳng và là
Bài 5: Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ: Bốn đồ thị nói trên cắt nhau tại các điểm O(0; 0), A, B, C. Tứ giác có 4 đỉnh O, A, B, C là hình gì?
Đáp án : A
Với hàm số y = x, cho x = 1 thì y = 1. Đồ thị hàm số y = x đi qua các điểm O(0;0) và C(1;1)
Với hàm số y = x+2, cho x = 0 thì y = 2, cho x = -1 thì y = 1. Đồ thị hàm số y = x +2 đi qua các điểm B(0;2) và A(-1;1)
Với hàm số y = -x, cho x = -1 thì y = 1. Đồ thị hàm số y = -x đi qua các điểm O(0;0) và A(-1;1)
Với hàm số y = -x +2, cho x =0 thì y = 2, cho x = 1 thì y = 1. Đồ thị hàm số y = -x +2 đi qua các điểm B (0;2) và C(1;1)
Đồ thị hàm số:
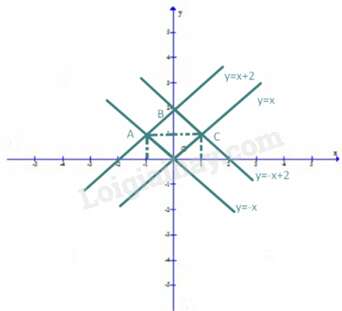
Từ đồ thị trên ta thấy:
Đường thẳng song song với đường thẳng nên OC//AB
Đường thẳng song song với đường thẳng nên OA//BC
Tứ giá OABC có: OC//AB, OA//BC và nên tứ giác OABC là hình thoi
Bài 6: Trong các hình vẽ dưới đây, hình vẽ nào là đồ thị của hàm số ?
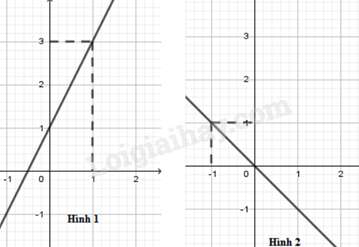
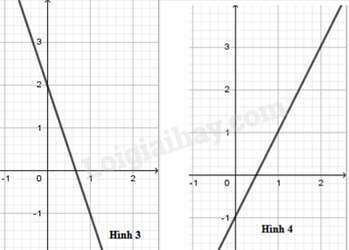
Đáp án : B
Đồ thị của hàm số đi qua các điểm có tọa độ (0; 1) và nên hình 1 là đồ thị của hàm số
Bài 7: Cho đường thẳng d: Đường thẳng d đi qua điểm A(1; 5). Chọn đáp án đúng.
Đáp án : C
Đường thẳng d đi qua điểm A(1; 5) nên
B. Lý thuyết Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)
1. Đồ thị của hàm số bậc nhất
Định nghĩa:
Đồ thị của hàm số y = ax + b (a ≠ 0) là một đường thẳng.
Chú ý:
- Đồ thị của hàm số y = ax + b (a ≠ 0) còn được gọi là đường thẳng y = ax + b (a ≠ 0).
- Đồ thị của hàm số y = ax + b (a ≠ 0) là một đường thẳng cắt trục tung tại điểm có tung độ bằng b.
Ví dụ: Đồ thị dưới đây là đồ thị của hàm số bậc nhất y = 2x −1.
2. Cách vẽ đồ thị của hàm số bậc nhất
2.1. Cách vẽ đồ thị hàm số y = ax (a ≠ 0)
Cách vẽ:
Để vẽ đồ thị của hàm số y = ax (a ≠ 0), ta có thể xác định điểm A(1; a) rồi vẽ đường thẳng đi qua hai điểm O và A.
Ví dụ: Vẽ đồ thị của hàm số y = −2x.
Hướng dẫn giải
Với x = 1 thì y = −2, ta được A(1; −2) thuộc đồ thị hàm số y = −2x.
Vậy đồ thị của hàm số y = −2x là đường thẳng đi qua hai điểm O(0; 0) và A(1; −2).
2.2. Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0; b ≠ 0)
Cách vẽ:
Để vẽ đồ thị của hàm số y = ax + b (a ≠ 0; b≠ 0), ta có thể xác định hai điểm P(0; b) và Q rồi vẽ đường thẳng đi qua hai điểm đó.
Ví dụ: Vẽ đồ thị của hàm số y = −2x + 2.
Hướng dẫn giải
Với x = 0 thì y = 2, ta được điểm P(0; 2) thuộc đồ thị của hàm số y = −2x + 2.
Với y = 0 thì x = 1, ta được điểm Q(1; 0) thuộc đồ thị của hàm số y = −2x + 2.
Vẽ đồ thị của hàm số y = −2x + 2 là đường thẳng đi qua hai điểm P(0; 2), Q(1; 0).
3. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)
3.1. Góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox
Trong mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a ≠0). Gọi A là giao điểm của đường thẳng y = ax + b và trục Ox. T là một điểm thuộc đường thẳng y = ax + b và có tung độ dương.
Góc α tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox (hoặc nói đường thẳng y = ax + b tạo với trục Ox một góc α).
3.2. Hệ số góc
Định nghĩa:
Trên mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a ≠ 0). Hệ số a gọi là hệ số góc của đường thẳng y = ax + b (a ≠ 0).
Chú ý:
- Khi hệ số a > 0 thì góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox là góc nhọn. Hệ số a càng lớn thì góc càng lớn.
- Khi hệ số a < 0 thì góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox là góc tù. Hệ số a càng lớn thì góc càng lớn.
Ví dụ:
Hệ số góc của đường thẳng y = 2x + 1 là 2.
Hệ số góc của đường thẳng y = −x + 3 là −1.
3.3. Ứng dụng của hệ số góc
Cách nhận biết vị trí tương đối của hai đường thẳng trong mặt phẳng tọa độ Oxy:
Cho hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0).
a) Nếu d song song với d’ thì a = a’; b ≠ b’. Ngược lại, nếu a = a’; b ≠ b’ thì d song song với d’.
b) Nếu d trùng với d’ thì a = a’; b = b’. Ngược lại, nếu a = a’; b = b’ thì d trùng với d’.
c) Nếu d và d’ cắt nhau thì a ≠ a’. Ngược lại, nếu a ≠ a’ thì d và d’ cắt nhau.
Ví dụ:
- Hai đường thẳng y = 2x + 1; y = 2x + 3 có hệ số góc bằng nhau và hệ số tự do khác nhau nên hai đường thẳng này song song.
- Hai đường thẳng y = 2x + 1; y = 3x có hệ số góc khác nhau nên hai đường thẳng này cắt nhau.
- Hai đường thẳng y = 3x – 1; y = 3x −1 có hệ số góc và hệ số tự do giống nhau nên hai đường thẳng này trùng nhau.
tran minh
2026-02-23 20:42:31
good=]]]]