Với giải sách bài tập Toán 8 Bài 1: Hình chóp tam giác đều sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 1: Hình chóp tam giác đều

Giải SBT Toán 8 trang 73

Bài 1 trang 73 SBT Toán 8 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu sai? Vì sao?

a) Hình chóp tam giác đều có 6 mặt

b) Hình chóp tam giác đều có 3 cạnh đáy bằng nhau.

c) Hình chóp tam giác đều có 8 đỉnh

d) Hình chóp tam giác đều có các mặt bên là những tam giác cân.

Lời giải:

Hình chóp tam giác đều $S.ABC$ có đỉnh $S$ và 4 mặt. Trong đó, 1 mặt đáy là tam giác $ABC$ đều, 3 mặt bên là những tam giác cân $SAB,SBC,SAC$. Vậy các phát biểu đúng là: b,d; các phát biểu sai: a,c.

Bài 2 trang 73 SBT Toán 8 Tập 1: Trong các phát biểu sau, phát biểu nào đúng?

a) Diện tích xung quanh của hình chóp tam giác đều bằng nửa tích của chu vi đáy với độ dài trung đoạn.

b) Diện tích xung quanh của hình chóp tam giác đều bằng nửa tích của chu vi đáy với chiều cao.

c) Diện tích xung quanh của hình chóp tam giác đều bằng tích của chu vi đáy với độ dài trung đoạn.

d) Diện tích xung quanh của hình chóp tam giác đều bằng nửa tổng của chu vi đáy với độ dài trung đoạn. 

Lời giải:

Diện tích xung quanh của hình chóp tam giác đều bằng nửa tích của chu vi đáy với độ dài trụng đoạn.

→   Phát biểu a là đúng.

Bài 3 trang 73 SBT Toán 8 Tập 1: Cho hình chóp tam giác đều có độ dài cạnh đáy bằng 10 cm và độ dài trung đoạn bằng 9 cm. Tính diện tích xung quanh của hình chóp tam giác đều đó.

Lời giải:

Diện tích xung quanh của hình chóp tam giác đều đó là:

$S_{xq}=\frac{1}{2}.\left(10.3\right).9=135\left(c{m}^2\right)$.

Bài 4 trang 73 SBT Toán 8 Tập 1: Cho hình chóp tam giác đều có thể tích bằng 30 cm³ và chiều cao bằng 12 cm. Tính diện tích đáy của hình chóp tam giác đều đó.

Lời giải:

Áp dụng công thức $V=\frac{1}{3}.S.h$, trong đó $V$ là thể tích, $S$ là diện tích đáy, $h$ là chiều cao của hình chóp tam giác đều, ta có: $30=\frac{1}{3}.S.12$.

Suy ra $S=7,5\left(c{m}^2\right)$.

Vậy diện tích đáy của hình chóp tam giác đều đó là $7,5c{m}^2$.

Giải SBT Toán 8 trang 74

Bài 5 trang 74 SBT Toán 8 Tập 1: Cho hình chóp tam giác đều $S.ABC$ có độ dài cạnh đáy bằng 9 cm, $SH$ là chiều cao. Gọi $M$ là trung điểm của $BC$ (Hình 5). Tính thể tích của hình chóp $S.ABC$, biết $H$ là trọng tâm của tam giác $ABC$, $AH=\frac{\sqrt{3}}{3}AB$ và $SH=2AH$.

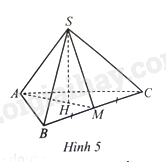
Lời giải:

Ta có: $AH=\frac{\sqrt{3}}{3}AB$ nên $AH=3\sqrt{3}$ cm. Suy ra $SH=2AH=6\sqrt{3}$ cm.

Do $H$ là trọng tâm của tam giác $ABC$ nên $AH=\frac{2}{3}AM$.

Suy ra $AM=\frac{3}{2}AH=\frac{9\sqrt{3}}{2}$ cm.

$\mathrm{\Delta }ABM=\mathrm{\Delta }ACM$(c-c-c) suy ra $\widehat{AMB}=\widehat{AMC}={90}^{\circ }$. Do đó $AM\mathrm{\perp }BC$.

Diện tích của hình chóp tam giác đều đó là:

$S_{ABC}=\frac{1}{2}.BC.AM=\frac{81\sqrt{3}}{4}\left(c{m}^2\right)$

Thể tích của hình chóp tam giác đều đó là: $\frac{1}{3}.S_{ABC}.SH=\frac{243}{2}\left(c{m}^2\right)$.

Bài 6 trang 74 SBT Toán 8 Tập 1: Bạn Nam có hai hộp quà có dạng hình chóp tam giác đều. Hộp quà thứ nhất có độ dài cạnh đáy bằng 30 cm và độ dài trung đoạn bằng 24 cm. Hộp quà thứ hai có độ dài cạnh đáy bằng 35 cm và độ dài trung đoạn bằng 32 cm. Bạn Nam dự định dán giấy màu bên ngoài cả ba mặt xung quanh của mỗi hộp quà: Hộp quà thứ nhất dán giấy màu đỏ có giá 35 000 đồng/m²; Hộp quà thứ hai dán giấy màu xanh có giá 25 000 đồng/m².

a)     Với số tiền 10 000 đồng, bạn Nam có thể dán giấy màu vào cả hai hộp quà như dự định hay không? Vì sao?

b)    Bạn Nam nhận định: “Diện tích xung quanh của hộp quà thứ nhất bằng 70% diện tích xung quanh của hộp quà thứ hai”. Nhận định của bạn Nam có đúng hay không? Vì sao?

Lời giải:

Đổi: $30cm=0,3m;24cm=0,24m;35cm=0,35m;32cm=0,32m$.

a) Diện tích xung quanh của hộp quà thứ nhất là: $\frac{1}{2}.\left(0,3.3\right).0,24=0,108\left(m^2\right)$

Diện tích xung quanh của hộp quà thứ hai là: $\frac{1}{2}.\left(0,35.3\right).0,32=0,168\left(m^2\right)$

Số tiền bạn Nam cần trả để mua giấy màu dán hai hộp quà là:

$0,108.35000+0,168.25000=7980$ (đồng)

Do 7 980 < 10 000 nên với số tiền 10 000 đồng, bạn Nam có thể dán giấy màu vào cả hai hộp quà như dự định.

b)    Tỉ số phần trăm giữa diện tích xung quanh của hộp quà thứ nhất và diện tích xung quanh của hộp quà thứ hai là:

$\frac{0,108.100}{0,168}\mathrm{\%}\approx 64,3\mathrm{\%}$

Vậy nhận định của bạn Nam là sai.

Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 3

Bài 1: Hình chóp tam giác đều

Bài 2: Hình chóp tứ giác đều

Bài tập cuối chương 4

Bài 1: Định lí Pythagore

Lý thuyết Hình chóp tam giác đều

1. Khái niệm 

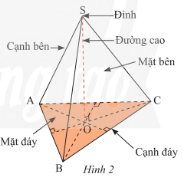
Hình chóp tam giác đều có 4 mặt, 6 cạnh:

- Đáy là tam giác đều.

- 3 cạnh bên bằng nhau.

- 3 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.

- 3 cạnh đáy bằng nhau là ba cạnh của tam giác đáy.

- Chân đường cao trùng với tâm của đáy.

2. Công thức tính diện tích xung quanh của hình chóp tam giác đều

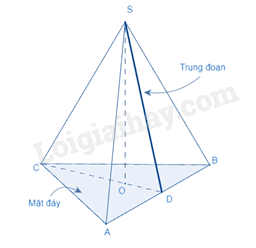
Diện tích xung quanh của hình chóp tam giác đều bằng nửa chu vi đáy với độ dài trung đoạn.

$Sxq=p.d$ 

(là diện tích xung quanh, p là nửa chu vi đáy, d là trung đoạn)

Công thức tính thể tích của hình chóp tam giác đều

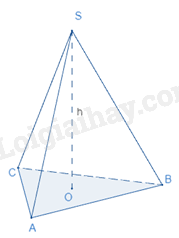
Thể tích của hình chóp tam giác đều bằng diện tích đáy nhân với chiều cao.

$V=\frac{1}{3}.h.S{­}_{đáy}$

(V là thể tích, $S{­}_{đáy}$ là diện tích đáy, h là chiều cao)

Ví dụ: 

Cho hình chóp tam giác đều sau:

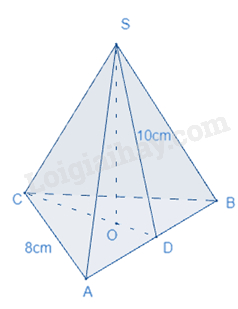
Diện tích xung quanh của hình chóp là:

$S_{xq}=\frac{3.8}{2}.10=120(c{m}^2)$

Cho hình chóp tam giác đều sau:

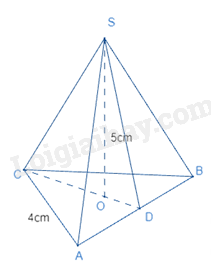
Chiều cao của mặt đáy là:

$CD=\sqrt{4^2-{\left(\frac{4}{2}\right)}^2}=2\sqrt{3}(cm)$

Thể tích của hình chóp là:

$V=\frac{1}{3}.5.\frac{4.2\sqrt{3}}{2}=\frac{20\sqrt{3}}{3}(c{m}^3)$