Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 8 Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a khác 0) chi tiết sách Toán 8 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a khác 0)
Video bài giải Toán lớp 8 Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a khác 0) - Cánh diều
Đồ thị của hàm số bậc nhất y = ax + b (a ≠ 0) có tính chất gì?
Lời giải:
Sau khi học xong bài này ta sẽ giải quyết bài toán này như sau:
Đồ thị hàm số y = ax + b (a ≠ 0) là một đường thẳng.
• Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng hay đồ thị hàm số đi qua điểm
• Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng b hay đồ thị hàm số đi qua điểm (0; b).
I. Đồ thị của hàm số bậc nhất
Hoạt động 1 trang 71 Toán 8 Tập 1: Xét hàm số y = x – 2.
a) Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:
|
x |
0 |
2 |
3 |
|
y = x – 2 |
|
|
|
b) Vẽ các điểm A(0; − 2), B(2; 0), C(3; 1) của đồ thị hàm số y = x – 2 trong mặt phẳng tọa độ Oxy. Dùng thước thẳng để kiểm tra ba điểm A, B, C có thẳng hàng hay không.
Lời giải:
a) • Với x = 0 thì y = 0 – 2 = – 2;
• Với x = 2 thì y = 2 – 2 = 0;
• Với x = 3 thì y = 3 – 2 = 1.
Vậy giá trị của y tương ứng với giá trị của x được điền vào trong bảng sau:
|
x |
0 |
2 |
3 |
|
y = x – 2 |
– 2 |
0 |
1 |
b) Cách xác định các điểm trong mặt phẳng tọa độ Oxy là:
• Cách xác định điểm A(0; − 2):
Qua điểm − 2 trên trục Oy, ta kẻ đường thẳng vuông góc với trục Oy.
Đường thẳng thẳng này cắt trục Oy tại điểm A(0; − 2).
• Xác định điểm B(2; 0):
Qua điểm 2 trên trục Ox, ta kẻ đường thẳng vuông góc với trục Ox.
Đường thẳng thẳng này cắt trục Ox tại điểm B(2; 0).
• Xác định điểm C(3; 1):
Qua điểm 3 trên trục Ox, ta kẻ đường thẳng vuông góc với trục Ox.
Qua điểm 1 trên trục Oy, ta kẻ đường thẳng vuông góc với trục Oy.
Hai đường thẳng trên cắt nhau tại điểm C(3; 1).
Từ đó ta xác định các điểm A(0; − 2), B(2; 0), C(3; 1) trên trục số như sau:
Đặt thước thẳng để kiểm tra hai điểm A và B, ta thấy điểm C nằm trên đường thẳng đi qua hai điểm A và B.
Vậy ba điểm A, B, C có thẳng hàng.
Giải Toán 8 trang 72 Tập 1
Lời giải:
Điểm có hoành độ bằng 0, tức là điểm đó có x = 0.
Với x = 0 thì y = 4 . 0 + 3 = 0 + 3 = 3.
Vậy điểm thuộc đồ thị của hàm số có hoành độ bằng 0 thì tọa độ của điểm đó là (0; 3).
II. Vẽ đồ thị của hàm số bậc nhất
Luyện tập 2 trang 73 Toán 8 Tập 1: Vẽ đồ thị của mỗi hàm số sau:
a) y = 3x;
b) y = 2x + 2.
Lời giải:
a) Đồ thị hàm số y = 3x.
Với x = 1 thì y = 3 . 1 = 3, ta được điểm A(1; 3) thuộc đồ thị của hàm số y = 3x.
Vậy đồ thị của hàm số y = 3x là đường thẳng đi qua hai điểm O(0; 0) và A(1; 3).
Khi đó, đồ thị hàm số y = 3x được biểu diễn như hình vẽ:
b) Đồ thị hàm số y = 2x + 2.
• Với x = 0 thì y = 2 . 0 + 2 = 0 + 2 = 2, ta được điểm M(0; 2) thuộc đồ thị của hàm số y = 2x + 2.
• Với y = 0 thì 2x + 2 = 0 suy ra x = – 1, ta được điểm N(– 1; 0) thuộc đồ thị của hàm số y = 2x + 2.
Vậy đồ thị của hàm số y = 2x + 2 là đường thẳng đi qua hai điểm M(0; 2) và N(– 1; 0).
Khi đó, đồ thị hàm số y = 2x + 2 được biểu diễn như hình vẽ:
III. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)
Hoạt động 2 trang 73 Toán 8 Tập 1: Quan sát các đường thẳng y = x + 1 và y = – x – 1 (Hình 20).
a) Tung độ các điểm M, N là số dương hay số âm?
b) Tìm góc tạo bởi hai tia Ax và AM ở Hình 20a.
c) Tìm góc tạo bởi hai tia Bx và BN ở Hình 20b.
Lời giải:
a) Trong Hình 20a): Điểm M nằm trong góc phần tư thứ nhất nên tung độ các điểm M là số dương;
Trong Hình 20b): Điểm N nằm trong góc phần tư thứ hai nên tung độ các điểm N là số âm.
Vậy tung độ của điểm M là số dương và tung độ của điểm N là số âm.
b) Góc tạo bởi hai tia Ax và AM ở Hình 20a là góc MAx.
c) Góc tạo bởi hai tia Bx và BN ở Hình 20b là góc NBx.
Giải Toán 8 trang 76 Tập 1
Luyện tập 3 trang 75 Toán 8 Tập 1:Tìm hệ số góc của đường thẳng y = – 5x + 11.
Lời giải:
Hệ số góc của đường thẳng y = – 5x + 11 là – 5.
b) Quan sát Hình 23b, tìm hệ số góc của hai đường thẳng y = x và y = – x + 1 và nêu vị trí tương đối của hai đường thẳng đó.
Lời giải:
a) • Hệ số góc của hai đường thẳng y = x là 1;
• Hệ số góc của hai đường thẳng y = x + 1 là 1.
Trong Hình 23a) góc tạo bởi trục Ox và đường thẳng y = x bằng góc tạo bởi trục Ox và đường thẳng y = x + 1.
Mà hai góc này ở vị trí đồng vị nên ta suy ra hai đường thẳng y = x và y = x + 1 song song với nhau.
b) • Hệ số góc của hai đường thẳng y = x là 1;
• Hệ số góc của hai đường thẳng y = – x + 1 là – 1.
Trong Hình 23b) hai đường thẳng y = x và y = – x + 1 cắt nhau.
Lời giải:
• Đường thẳng y = – 5x có hệ số góc bằng – 5 và hệ số tự do bằng 0.
• Đường thẳng y = – 5x + 2 có hệ số góc bằng – 5 và hệ số tự do bằng 2.
Hai đường thẳng y = – 5x và y = – 5x + 2 có hệ số góc bằng nhau và hệ số tự do khác nhau nên hai đường thẳng đó song song.
Bài tập
a) Đường thẳng d cắt trục tung tại điểm có tung độ bằng .
b) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng b.
c) Đường thẳng d cắt trục tung tại điểm có tung độ bằng b.
d) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng .
Lời giải:
• Đường thẳng d cắt trục tung, tức là y = 0 nên ta có ax + b = 0.
Suy ra ax = – b hay x =
Khi đó, đường thẳng d cắt trục tung tại điểm có tung độ bằng .
Do đó, phát biểu a) đúng, phát biểu c) sai.
• Đường thẳng d cắt trục hoành, tức là x = 0 nên ta có y = a . 0 + b = 0 + b = b.
Khi đó, đường thẳng d cắt trục hoành tại điểm có hoành độ bằng b.
Do đó, phát biểu b) đúng, phát biểu d) sai.
Lời giải:
• Đường thẳng y = – 2x + 5 có hệ số góc bằng – 2 và hệ số tự do bằng 5.
• Đường thẳng y = – 2x có hệ số góc bằng – 2 và hệ số tự do bằng 0.
• Đường thẳng y = 4x – 1 có có hệ số góc bằng 4 và hệ số tự do bằng – 1.
Hai đường thẳng y = – 2x + 5 và y = – 2x có hệ số góc bằng nhau và hệ số tự do khác nhau nên hai đường thẳng này song song.
Hai đường thẳng y = – 2x + 5 và y = 4x – 1 có hệ số góc khác nhau nên hai đường thẳng này cắt nhau.
Hai đường thẳng y = – 2x và y = 4x – 1 có hệ số góc khác nhau nên hai đường thẳng này cắt nhau.
Vậy các cặp đường thẳng cắt nhau là: y = – 2x + 5 và y = 4x – 1; y = – 2x và y = 4x – 1; các cặp đường thẳng song song là y = – 2x + 5 và y = – 2x.
Lời giải:
* Đồ thị hàm số y = 3x.
Với x = 1 thì y = 3 . 1 = 3, ta được điểm A(1; 3) thuộc đồ thị của hàm số y = 3x.
Do đó, đồ thị của hàm số y = 3x là đường thẳng đi qua hai điểm O(0; 0) và A(1; 3).
* Đồ thị hàm số y = 3x + 4.
• Với x = 0 thì y = 3 . 0 + 4 = 0 + 4 = 4, ta được điểm B(0; 4) thuộc đồ thị của hàm số y = 3x + 4.
• Với y = 0 thì 3x + 4 = 0 suy ra , ta được điểm thuộc đồ thị của hàm số y = 3x + 4.
Do đó, đồ thị của hàm số y = 2x + 2 là đường thẳng đi qua hai điểm B(0; 4) và
* Đồ thị hàm số .
Với x = 2 thì , ta được điểm M(2; – 1) thuộc đồ thị của hàm số .
Do đó, đồ thị của hàm số là đường thẳng đi qua hai điểm O(0; 0) và M(2; – 1).
* Đồ thị hàm số .
• Với x = 0 thì , ta được điểm N(0; 3) thuộc đồ thị của hàm số
• Với y = 0 thì suy ra x = 6, ta được điểm P(6; 0) thuộc đồ thị của hàm số
Do đó, đồ thị của hàm số là đường thẳng đi qua hai điểm N(0; 3) và P(6; 0).
Ta vẽ đồ thị của các hàm số y = 3x; y = 3x + 4; trên cùng một mặt phẳng tọa độ như sau:
Lời giải:
Theo đề bài, đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng – 1 nên đường thẳng có dạng y = – x + b.
Mặt khác, đường thẳng đi qua điểm M(1; 2) nên ta có:
– 1 + b = 2 suy ra b = 3.
Do đó, đường thẳng cần tìm là y = – x + 3.
• Với x = 0 thì y = – 0 + 3 = 0 + 3 = 3, ta được điểm A(0; 3) thuộc đồ thị của hàm số y = – x + 3.
• Với y = 0 thì – x + 3 = 0 suy ra x = 3, ta được điểm B(3; 0) thuộc đồ thị của hàm số y = – x + 3.
Do đó, đồ thị của hàm số y = – x + 3 là đường thẳng đi qua hai điểm A(0; 3) và B(3; 0).
Ta vẽ đồ thị hàm số như sau:
Bài 5 trang 77 Toán 8 Tập 1: a) Vẽ đường thẳng y = 2x – 1 trong mặt phẳng tọa độ.
b) Xác định đường thẳng y = ax + b (a ≠ 0) đi qua điểm M(1; 3) và song song với đường thẳng y = 2x – 1. Sau đó vẽ đường thẳng tìm được trên mặt phẳng tọa độ.
Lời giải:
a) Đường thẳng y = 2x – 1.
• Với x = 0 thì y = 2 . 0 – 1 = 0 – 1 = – 1, ta được điểm A(0; – 1) thuộc đồ thị của hàm số y = 2x – 1.
• Với y = 0 thì 2x – 1 = 0 suy ra , ta được điểm thuộc đồ thị của hàm số y = 2x – 1.
Do đó, đồ thị của hàm số y = 2x – 1 là đường thẳng đi qua hai điểm A(0; – 1) và
Ta vẽ đồ thị hàm số y = 2x – 1 như sau:
b) Đường thẳng y = ax + b (a ≠ 0) song song với đường thẳng y = 2x – 1 nên đường thẳng có dạng y = 2x + b.
Mặt khác, đường thẳng y = 2x + b đi qua điểm M(1; 3) nên 2 . 1 + b = 3 suy ra b = 1.
Do đó, đường thẳng cần tìm là y = 2x + 1.
• Với x = 0 thì y = 2 . 0 + 1 = 0 + 1 = 1, ta được điểm C(0; 1) thuộc đồ thị của hàm số y = 2x + 1.
• Với y = 0 thì 2x + 1 = 0 suy ra , ta được điểm thuộc đồ thị của hàm số y = 2x + 1.
Do đó, đồ thị của hàm số y = 2x + 1 là đường thẳng đi qua hai điểm C(0; 1) và
Ta vẽ đồ thị hàm số y = 2x + 1 như sau:
a) Nêu nhận xét về tung độ giao điểm của hai đường thẳng d1, d2. Từ đó, nêu nhận xét về tốc độ ban đầu của hai chuyển động.
b) Trong hai đường thẳng d1, d2, đường thẳng nào có hệ số góc lớn hơn?
c) Từ giây thứ nhất trở đi, vật nào có tốc độ lớn hơn? Vì sao?
Lời giải:
a) Tung độ giao điểm của hai đường thẳng d1, d2 hay hai đường thẳng d1, d2 đều cắt trục tung tại điểm có tung độ bằng 2.
Do đó, tốc độ ban đầu của hai chuyển động bằng nhau.
b) Qua điểm 2 trên trục tung, ta kẻ đường thẳng d // Ox (như hình vẽ).
Trong hình vẽ, ta thấy góc tạo bởi đường thẳng d và đường thẳng d2 lớn hơn góc tạo bởi đường thẳng d và đường thẳng d1.
Mà d // Ox nên suy ra góc tạo bởi đường thẳng Ox và đường thẳng d2 lớn hơn góc tạo bởi đường thẳng Ox và đường thẳng d1.
Do đó, trong hai đường thẳng d1, d2, đường thẳng d2 có hệ số góc lớn hơn.
c)
Trên hai đường thẳng d1, d2 ta lấy hai điểm M, N bất kì có cùng hoành độ (với t > 1), ta kẻ hai đường thẳng vuông góc với trục tung.
Do đó, tung độ của điểm N lớn hơn tung độ của điểm M.
Khi đó, vật thứ hai có tốc độ lớn hơn.
Vậy từ giây thứ nhất trở đi, vật thứ hai có tốc độ lớn hơn.
Xem thêm các bài giải SGK Toán lớp 8 Cánh diều hay, chi tiết khác:
Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0)
Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)
Lý thuyết Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)
1. Đồ thị của hàm số bậc nhất
Đồ thị của hàm số y = ax + b (a0) là một đường thẳng.
Chú ý: Đồ thị hàm số y = ax + b (a0) còn gọi là đường thẳng y = ax + b (a0).
Ví dụ: Cho hàm số y = 2x – 3 có hai điểm A(1, -1) và B(2; 1) thuộc đồ thị của hàm số y = 2x – 3.
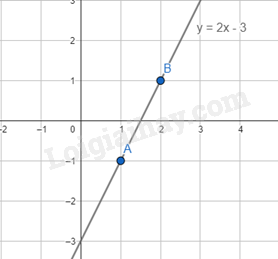
2. Vẽ đồ thị của hàm số bậc nhất
Hàm số y = ax (a0)
Để vẽ đồ thị của hàm số y = ax (a0), ta có thể xác định điểm A(1; a) rồi vẽ đường thẳng đi qua hai điểm O và A.
Hàm số y = ax + b (a0)
Để vẽ đồ thị của hàm số y = ax + b (a0, b0), ta có thể xác định hai điểm P(0; b) và Q rồi vẽ dường thẳng đi qua hai điểm đó.
Ví dụ: Cho hàm số y = -2x + 4
Với x = 0 thì y = 4, ta được điểm P(0;4)
Với y = 0 thì x = 22, ta được điểm Q(2;0)
Vậy đồ thị hàm số y = -2x + 4 là đường thẳng đi qua hai điểm P(0;4) và Q(2;0)
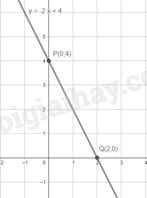
3. Hệ số góc của đường thẳng y = ax + b (a0)
Góc tạo bởi đường thẳng y = ax + b (a0) và trục Ox.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a0). Gọi A là giao điểm của đường thẳng y = ax + b và trục Ox, T là một điểm thuộc đường thẳng y = ax + b và có tung độ dương.
Góc tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox (hoặc nói đường thẳng y = ax + b tạo với trục Ox một góc )
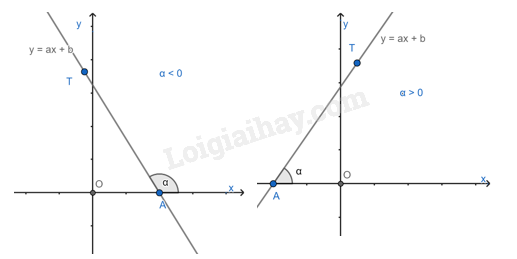
Hệ số góc
Trên mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a0). Hệ số a gọi là hệ số góc của đường thẳng y = ax + b (a0).
Nhận xét:
Khi hệ số góc a > 0 thì góc tạo bởi đường thẳng y = ax + b (a0) và trục Ox là góc nhọn. Hệ số a càng lớn thì góc càng lớn.
Khi hệ số góc a < 0 thì góc tạo bởi đường thẳng y = ax + b (a0) và trục Ox là góc tù. Hệ số a càng lớn thì góc càng lớn.
Ứng dụng của hệ số góc
Cho d: y = ax + b (a0) và d’: y = a’x + b’ (a’0)
a. d // d’ a = a’, b b’.
b.
c. d cắt d’ a a’
Ví dụ: y = 2x + 1, y = 2x + 3 là hai đường thẳng song song vì có hệ số góc bằng nhau và hệ số tự do khác nhau.