Với giải sách bài tập Toán 8 Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0) sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)
Giải SBT Toán 8 trang 61
Bài 21 trang 61 SBT Toán 8 Tập 1: Trong các phát biểu sau, phát biểu nào đúng?
a) Để vẽ đồ thị của hàm số , ta có thể xác định hai điểm và rồi vẽ đường thẳng đi qua hai điểm đó.
b) Để vẽ đồ thị của hàm số , ta có thể xác định hai điểm và rồi vẽ đường thẳng đi qua hai điểm đó.
c) Để vẽ đồ thị của hàm số , ta có thể xác định hai điểm và rồi vẽ đường thẳng đi qua hai điểm đó.
Lời giải:
Phát biểu a và c là phát biểu đúng.
Lời giải:
Gọi hệ số góc của các đường thẳng lần lượt là . Khi đó, ta có . Mà suy ra .
Vậy các góc được sắp xếp theo thứ tự tăng dần là: .
Bài 23 trang 62 SBT Toán 8 Tập 1: Cho hai đường thẳng và với và
a) Tìm giá trị của để đường thẳng đi qua điểm
b) Gọi là góc tạo bởi đường thẳng ở câu a và trục . Hỏi là góc nhọn hay góc tù? Tại sao?
c) Tìm giá trị của để cắt .
Lời giải:
a) Do đường thẳng đi qua điểm nên ta có: . Suy ra, . Vậy với thì đường thẳng đi qua điểm
b) Với , ta có đường thẳng . Suy ra hệ số góc của đường thẳng là . Vậy góc là góc tù.
c) Để và cắt nhau thì . Suy ra . Vậy với thì và cắt nhau.
Bài 24 trang 62 SBT Toán 8 Tập 1: Vẽ đồ thị của các hàm số trên cùng một mặt phẳng tọa độ.
Lời giải:
Xét hàm số . Với thì , ta được điểm thuộc đồ thị của hàm số . Vậy đồ thị của hàm số là đường thẳng đi qua hai điểm và .
Xét hàm số . Với thì , ta được điểm thuộc đồ thị của hàm số . Với thì , ta được điểm thuộc đồ thị của hàm số . Vậy đồ thị của hàm số là đường thẳng đi qua hai điểm và .
Tương tự ta có:
Đồ thị của hàm số là đường thẳng đi qua hai điểm và .
Đồ thị của hàm số là đường thẳng đi qua hai điểm và .
Ta vẽ các đồ thị trên:
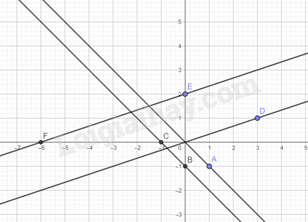
Lời giải:
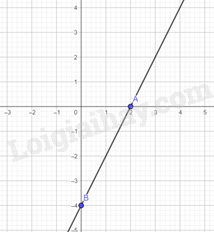
Do đường thẳng song song với đường thẳng nên (thỏa mãn) và . Mà đường thẳng đi qua điểm , suy ra hay (thỏa mãn). Do đó, đường thẳng cần tìm là .
Với thì , ta được điểm thuộc đồ thị của hàm số . Vậy đồ thị của hàm số là đường thẳng đi qua hai điểm và .
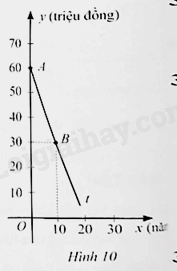
a) Chứng tỏ rẳng là hàm số bậc nhất của , tức là .
b) Trong Hình 10, tia là một phần của đường thẳng . Tìm . Từ đó, cho biết sau 12 năm sử dụng thì giá của thiết bị tiệt khuẩn đó bằng bao nhiêu phần trăm so với giá mua ban đầu.
Lời giải:
a) Công thức biểu thị giá của thiết bị tiệt khuẩn đó sau năm sử dụng là: hay . Mà , suy ra là hàm số bậc nhất của .
b) Từ câu a, ta có . Do đường thẳng đi qua điểm nên . Suy ra . Khi đó, đường thẳng cần tìm là: .
Giá của thiết bị tiệt khuẩn đó sau 12 năm sử dụng là:
(triệu đồng)
Tỉ số phần trăm giữa giá của thiết bị tiệt khuẩn đó sau 12 năm sử dụng và giá mua ban đầu là: .
Vậy sau 12 năm sử dụng thì giá của thiết bị tiệt khuẩn đó bằng so với giá mua ban đầu.
Bài 27 trang 62 SBT Toán 8 Tập 1: Cho đường thẳng với .
a) Tìm giá trị của để đường thẳng cùng với các trục tạo thành tam giác có diện tích bằng 2.
b) Chứng tỏ rằng khi giá trị của thay đổi thì tập hợp các đường thẳng luôn đi qua một điểm cố định.
Lời giải:
a) Với thì , ta được điểm là giao điểm của đường thẳng với trục . Khi đó .
Với thì , ta được điểm là giao điểm của đường thẳng với trục . Khi đó .
Ta có diện tích của tam giác bằng 2 nên hay .
Suy ra hay . Do đó hoặc .
Vậy hoặc (thỏa mãn) thì đường thẳng cùng với các trục tạo thành tam giác có diện tích bằng 2.
b) Từ câu a, ta có đường thẳng luôn đi qua điểm với mọi giá trị của . Vậy khi giá trị của thay đổi thì tập hợp các đường thẳng luôn đi qua điểm cố định.
Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác:
Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0)
Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)
Lý thuyết Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0)
1. Đồ thị của hàm số bậc nhất
Đồ thị của hàm số y = ax + b (a0) là một đường thẳng.
Chú ý: Đồ thị hàm số y = ax + b (a0) còn gọi là đường thẳng y = ax + b (a0).
Ví dụ: Cho hàm số y = 2x – 3 có hai điểm A(1, -1) và B(2; 1) thuộc đồ thị của hàm số y = 2x – 3.
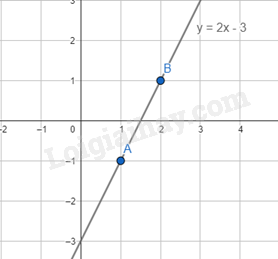
2. Vẽ đồ thị của hàm số bậc nhất
Hàm số y = ax (a0)
Để vẽ đồ thị của hàm số y = ax (a0), ta có thể xác định điểm A(1; a) rồi vẽ đường thẳng đi qua hai điểm O và A.
Hàm số y = ax + b (a0)
Để vẽ đồ thị của hàm số y = ax + b (a0, b0), ta có thể xác định hai điểm P(0; b) và Q rồi vẽ dường thẳng đi qua hai điểm đó.
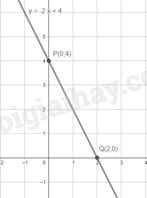
Ví dụ: Cho hàm số y = -2x + 4
Với x = 0 thì y = 4, ta được điểm P(0;4)
Với y = 0 thì x = 22, ta được điểm Q(2;0)
Vậy đồ thị hàm số y = -2x + 4 là đường thẳng đi qua hai điểm P(0;4) và Q(2;0)
3. Hệ số góc của đường thẳng y = ax + b (a0)
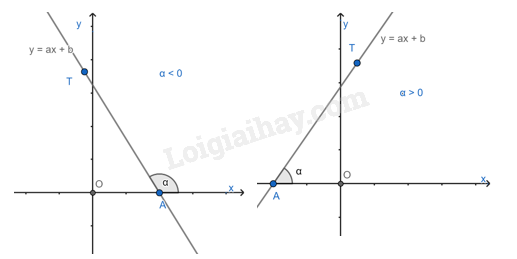
Góc tạo bởi đường thẳng y = ax + b (a0) và trục Ox.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a0). Gọi A là giao điểm của đường thẳng y = ax + b và trục Ox, T là một điểm thuộc đường thẳng y = ax + b và có tung độ dương.
Góc tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox (hoặc nói đường thẳng y = ax + b tạo với trục Ox một góc )
Hệ số góc
Trên mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a0). Hệ số a gọi là hệ số góc của đường thẳng y = ax + b (a0).
Nhận xét:
Khi hệ số góc a > 0 thì góc tạo bởi đường thẳng y = ax + b (a0) và trục Ox là góc nhọn. Hệ số a càng lớn thì góc càng lớn.
Khi hệ số góc a < 0 thì góc tạo bởi đường thẳng y = ax + b (a0) và trục Ox là góc tù. Hệ số a càng lớn thì góc càng lớn.
Ứng dụng của hệ số góc
Cho d: y = ax + b (a0) và d’: y = a’x + b’ (a’0)
a. d // d’ a = a’, b b’.
b.
c. d cắt d’ a a’
Ví dụ: y = 2x + 1, y = 2x + 3 là hai đường thẳng song song vì có hệ số góc bằng nhau và hệ số tự do khác nhau.