Với giải sách bài tập Toán 7 Bài 1: Tập hợp các số hữu tỉ sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 1: Tập hợp các số hữu tỉ

Giải SBT Toán 7 trang 7 Tập 1

Bài 1 trang 7 sách bài tập Toán lớp 7 Tập 1: Thay dấu $\boxed{?}$ bằng kí hiệu ∈, ∉ thích hợp.

Lời giải:

∙ Vì −12 là số nguyên âm nên −12 không thuộc tập hợp số tự nhiên.

Do đó $-12\boxed{\notin }\mathbb{N}$;

∙ Vì −35 là số nguyên âm nên −12 thuộc tập hợp số nguyên.

Do đó $-35\boxed{\in }\mathbb{Z}$;

∙ Vì −78 là số nguyên âm nên −78 không thuộc tập hợp số tự nhiên.

Do đó $-78\boxed{\notin }\mathbb{N}$ ;

∙ Vì 7 $\cancel{⋮}$ 8 là số nguyên âm nên $\frac{7}{8}$ không thuộc tập hợp số tự nhiên.

Do đó $\frac{7}{8}\boxed{\notin }\mathbb{N}$ ;

∙ Vì 7; 8 $\in$ ℤ; 8 ≠ 0 nên $\frac{7}{8}$ là số hữu tỉ hay $\frac{7}{8}$ thuộc tập hợp ℚ.

Do đó $\frac{7}{8}\boxed{\in }\mathbb{Q}$ ;

∙ Vì 5,35 là số thập phân nên 5,35 không thuộc tập hợp số nguyên.

Do đó $5,35\boxed{\notin }\mathbb{Z}$;

∙ Ta có: $-2,35=\frac{-235}{100}$ mà −235; 100 $\in$ ℤ; 100 ≠ 0 nên $\frac{-235}{100}$ là số hữu tỉ.

Do đó $-2,35\boxed{\in }\mathbb{Q}$ .

Vậy ta điền vào ô trống như sau:

Bài 2 trang 7 sách bài tập Toán lớp 7 Tập 1: a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ $\frac{-4}{7}$?

$\frac{-8}{14};\frac{8}{14};\frac{12}{-21};-\frac{20}{35};\frac{-36}{62}$

b) Tìm số đối của mỗi số sau: 15;$\frac{-4}{7}$ ; −0,275; 0; $2\frac{1}{3}$.

Lời giải:

a) Ta có:

$\frac{-8}{14}=\frac{(-8):2}{14:2}=\frac{-4}{7}$; $\frac{8}{14}=\frac{8:2}{14:2}=\frac{6}{7}$;

$\frac{12}{-21}=\frac{-12}{21}=\frac{(-12):3}{21:3}=\frac{-4}{7}$; $-\frac{20}{35}=-\frac{20:5}{35:5}=-\frac{4}{7}=\frac{-4}{7}$;

$\frac{-36}{62}=\frac{(-36):2}{62:2}=\frac{-18}{31}$.

Vậy các phân số biểu diễn số hữu tỉ $\frac{-4}{7}$ là: $\frac{-8}{14};\frac{12}{-21};-\frac{20}{35}$.

b) Số đối của 15 là −15;

Số đối của $\frac{-4}{7}$ là $-\left(\frac{-4}{7}\right)=\frac{4}{7}$;

Số đối của −0,275 là – (–0,275) = 0,275;

Số đối của 0 là 0;

Số đối của $2\frac{1}{3}$ là $-2\frac{1}{3}$.

Vậy số đối của các số 15; $\frac{-4}{7}$; −0,275; 0; $2\frac{1}{3}$ lần lượt là −15; $\frac{4}{7}$; 0,275; 0; $-2\frac{1}{3}$.

Bài 3 trang 7 sách bài tập Toán lớp 7 Tập 1: a) Các điểm x, y, z trong hình dưới đây biểu diễn số hữu tỉ nào?

b) Biểu diễn các số hữu tỉ $\frac{-3}{4};1\frac{1}{4};\frac{1}{4};-1,5$ trên trục số.

Lời giải:

a) 

Từ điểm 0 đến điểm 1 được chia thành 5 đoạn thẳng bằng nhau, ta được đơn vị mới bằng $\frac{1}{5}$ đơn vị cũ.

∙ Điểm x trong hình trên nằm bên trái điểm 0 và cách 0 một đoạn bằng 6 đơn vị mới.

Do đó điểm x trong hình trên biểu diễn số hữu tỉ $\frac{-6}{5}$.

∙ Điểm y trong hình trên nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 2 đơn vị mới.

Do đó điểm y trong hình trên biểu diễn số hữu tỉ $\frac{2}{5}$.

∙ Điểm z trong hình trên nằm bên phải điểm 0 và cách 0 một đoạn bằng 9 đơn vị mới.

Do đó điểm y trong hình trên biểu diễn số hữu tỉ $\frac{9}{5}$.

Vậy các điểm x, y, z trong hình lần lượt biểu diễn các số hữu tỉ $\frac{-6}{5}$; $\frac{2}{5}$; $\frac{9}{5}$.

b) Ta có: $1\frac{1}{4}=\frac{5}{4};-1,5=\frac{-6}{4}$.

Chia đoạn thẳng đơn vị thành 4 đoạn thẳng bằng nhau, ta được đơn vị mới bằng $\frac{1}{4}$ đơn vị cũ.

∙ Số hữu tỉ $\frac{-3}{4}$ nằm bên trái điểm 0 và cách điểm 0 một khoảng bằng 3 đơn vị mới.

∙ Số hữu tỉ $1\frac{1}{4}$ hay số hữu tỉ $\frac{5}{4}$ nằm bên phải điểm 0 và cách điểm 0 một khoảng bằng 5 đơn vị mới.

∙ Số hữu tỉ $\frac{1}{4}$ nằm bên phải điểm 0 và cách điểm 0 một khoảng bằng 1 đơn vị mới.

∙ Số hữu tỉ −1,5 hay số hữu tỉ $\frac{-6}{4}$ nằm bên trái điểm 0 và cách điểm 0 một khoảng bằng 6 đơn vị mới.

Vậy biểu diễn các số hữu tỉ $\frac{-3}{4};1\frac{1}{4};\frac{1}{4};-1,5$ trên trục số như sau:

Bài 4 trang 7 sách bài tập Toán lớp 7 Tập 1: a) Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?

$\frac{5}{14};-\frac{3}{5};1\frac{2}{5};-3;\frac{0}{176};-0,72$

b) Hãy sắp xếp các số trên theo thứ tự từ bé đến lớn.

Lời giải:

a) Ta thấy: $\frac{5}{14}>0;1\frac{2}{5}>0;$

$-\frac{3}{5}<0;-3<0;-0,72<0;\frac{0}{176}=0$

Vậy các số hữu tỉ dương là $\frac{5}{14};1\frac{2}{5}$; các số hữu tỉ âm là $-\frac{3}{5};-3;-0,72$ và số không là số hữu tỉ dương cũng không là số hữu tỉ âm là $\frac{0}{176}$.

b) Ta có: $\frac{0}{176}=0$.

∙ Nhóm các số hữu tỉ dương: $\frac{5}{14};1\frac{2}{5}$.

Vì $\frac{5}{14}<1$ và $1\frac{2}{5}>1$ nên $\frac{5}{14}<1\frac{2}{5}$.

∙ Nhóm các số hữu tỉ âm: $-\frac{3}{5};-3;-0,72$.

Ta có: $-\frac{3}{5}=-0,6$.

Số đối của các số −0,6; −3; −0,72 lần lượt là 0,6; 3; 0,72.

Vì 3 > 0,72 > 0,6 nên −3 < −0,72 < −0,6.

Do đó $-3<-0,72<-\frac{3}{5}$.

Từ đó ta suy ra: $-3<-0,72<-\frac{3}{5}<0<\frac{5}{14}<1\frac{2}{5}$.

Vậy các số trên được theo thứ tự từ bé đến lớn là $-3;-0,72;-\frac{3}{5};0;\frac{5}{14};1\frac{2}{5}$.

Bài 5 trang 7 sách bài tập Toán lớp 7 Tập 1:So sánh các cặp số hữu tỉ sau:

a) $\frac{2}{-3}$ và $\frac{-3}{5}$;

b) 0,65 và $\frac{13}{20}$;

c) −4,85 và −3,48;

d) $-1\frac{2}{9}$ và $-\left(\frac{-11}{-9}\right)$.

Lời giải:

a) $\frac{2}{-3}$ và $\frac{-3}{5}$;

Ta có: $\frac{2}{-3}=\frac{-2}{3}=\frac{-10}{15}$; $\frac{-3}{5}=\frac{-9}{15}$.

Vì −10 < −9 nên $\frac{-10}{15}<\frac{-9}{15}$ hay $\frac{2}{-3}<\frac{-3}{5}$.

Vậy $\frac{2}{-3}<\frac{-3}{5}$.

b) 0,65 và $\frac{13}{20}$;

Ta có $0,65=\frac{65}{100}=\frac{13}{20}$.

Vậy $0,65=\frac{13}{20}$.

c) −4,85 và −3,48

Số đối của −4,85 và −3,48 lần lượt là 4,85 và 3,48.

Vì 4,85 > 3,48 nên −4,85 < −3,48.

Vậy −4,85 < −3,48.

d) $-1\frac{2}{9}$ và $-\left(\frac{-11}{-9}\right)$.

Ta có: $-1\frac{2}{9}=\frac{-11}{9}$; $-\left(\frac{-11}{-9}\right)=\frac{-11}{9}$.

Vậy $-1\frac{2}{9}=-\left(\frac{-11}{-9}\right)$.

Giải SBT Toán 7 trang 7 Tập 1

Bài 6 trang 8 sách bài tập Toán lớp 7 Tập 1:So sánh các cặp số hữu tỉ sau:

a) $\frac{-2}{7}$ và $\frac{1}{300}$;

b) $\frac{237}{236}$ và $\frac{2385}{2386}$;

c) $\frac{-22}{33}$ và $\frac{50}{-77}$.

Lời giải:

a) $\frac{-2}{7}$ và $\frac{1}{300}$;

Ta có: $\frac{-2}{7}$ < 0; $\frac{1}{300}$ > 0 nên $\frac{-2}{7}$ < $\frac{1}{300}$.

Vậy $\frac{-2}{7}$ < $\frac{1}{300}$.

b) $\frac{237}{236}$ và $\frac{2385}{2386}$;

Vì $\frac{237}{236}>1$ (phân số có tử số lớn hơn mẫu số thì phân số đó lớn hơn 1);

$\frac{2385}{2386}$ < 1 (phân số có tử số bé hơn mẫu số thì phân số đó bé hơn 1).

Do đó $\frac{237}{236}>1$ > 1 > $\frac{2385}{2386}$.

Vậy $\frac{237}{236}>1$ > $\frac{2385}{2386}$.

c) $\frac{-22}{33}$ và $\frac{50}{-77}$.

Ta có: $\frac{-22}{33}=\frac{-154}{231}$; $\frac{50}{-77}=\frac{-50}{77}=\frac{-150}{231}$.

Vì −154 < −150 nên $\frac{-154}{231}$ < $\frac{-150}{231}$ hay $\frac{-22}{33}$ < $\frac{50}{-77}$.

Vậy $\frac{-22}{33}$ < $\frac{50}{-77}$.

Bài 7 trang 8 sách bài tập Toán lớp 7 Tập 1: Ở vòng 1 cuộc thi tìm hiểu về bảo vệ môi trường, bạn Huy đã trả lời được 92% số câu trắc nghiệm. Ở vòng 2, bạn Huy đã trả lời đúng được 27 câu trong số 30 câu trắc nghiệm. Trong hai vòng thi, vòng nào bạn Huy làm bài tốt hơn?

Lời giải:

Tỉ số phần trăm số câu trả lời đúng của bạn Huy trong vòng 2 là:

$\frac{27}{30}.100\%=90\%$

Vì 92% > 90% nên vòng 1 bạn Huy làm bài tốt hơn.

Vậy trong hai vòng thi, vòng 1 bạn Huy làm bài tốt hơn.

Bài 8 trang 8 sách bài tập Toán lớp 7 Tập 1: Mực nước trong một cái ao so với mặt đất đo được trong các tháng được cho bởi bảng sau:

a) Trong các tháng trên tháng nào mực nước trong hồ cạn nhất? Giải thích.

b) Trong các tháng trên tháng nào hồ đầy nước nhất? Giải thích.

Lời giải:

∙ Nhóm các số hữu tỉ âm: −1,4; −1,8; −1,5.

Số đối của các số −1,4; −1,8; −1,5 lần lượt là 1,4; 1,8; 1,5.

Vì 1,8 > 1,5 > 1,4 nên −1,8 < −1,5 < −1,4.

∙ Nhóm số hữu tỉ dương: 0,95.

Do đó −1,8 < −1,5 < −1,4 < 0,95.

a) Tháng 6 có mực nước trong hồ cạn nhất vì có mực nước trong ao thấp nhất  là −1,8 m.

b) Tháng 9 hồ đầy nước nhất vì có mực nước trong ao cao nhất là 0,95 m.

Xem thêm các bài giải SBT Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Tập hợp các số hữu tỉ

Bài 2: Các phép tính với số hữu tỉ

Bài 3: Lũy thừa của một số hữu tỉ

Bài 4: Quy tắc dấu ngoặc và quy tắc chuyển vế

Bài tập cuối chương 1

Lý thuyết Tập hợp các số hữu tỉ

1. Số hữu tỉ

– Số hữu tỉ là số được viết dưới dạng phân số $\frac{a}{b}$ với a, b ∈ ℤ, b ¹ 0.

– Các phân số bằng nhau biểu diễn cùng một số hữu tỉ.

– Tập hợp các số hữu tỉ được kí hiệu là ℚ.

Ví dụ:

• Các số $\frac{4}{5};\frac{-9}{10};\frac{3}{-8}$ là các số hữu tỉ.

• Các số 5; −3,4; 3$\frac{2}{5}$ là các số hữu tỉ vì:

5 = $\frac{5}{1}$ = $\frac{10}{2}$ = …;

−3,4 = $\frac{-34}{10}$ = $\frac{-17}{5}$ = …;

3$\frac{2}{5}$= $\frac{17}{5}$ = $\frac{34}{10}$ = …

– Chú ý: Mỗi số nguyên là một số hữu tỉ.

2. Thứ tự trong tập hợp các số hữu tỉ

– Với hai số hữu tỉ bất kì x, y ta luôn có: hoặc x = y hoặc x < y hoặc x > y.

– Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương.

Số hữu tỉ bé hơn 0 gọi là số hữu tỉ âm.

Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.

Ví dụ: So sánh các cặp số hữu tỉ sau:

a) −0,8 và $\frac{-1}{5};$

b) −8$\frac{2}{3}$ và 0.

Hướng dẫn giải

a) −0,8 và $\frac{-1}{5}$

Ta có −0,8 = $\frac{-8}{10}$ và  $\frac{-1}{5}=\frac{-2}{10}$.

Vì −8 < −2 và 10 > 0 nên $\frac{-8}{10}<\frac{-2}{10}$.

Vậy – 0,8 < $\frac{-1}{5}$.

b) −8$\frac{2}{3}$ và 0

Ta có −8$\frac{2}{3}$= $\frac{-26}{3}$ và 0 = $\frac{0}{3}$.

Vì −26 < 0 và 3 > 0 nên  $\frac{-26}{3}<\frac{0}{3}$.

Vậy −8$\frac{2}{3}$ < 0.

Chú ý: Số hữu tỉ dương luôn luôn lớn hơn số hữu tỉ âm.

Ví dụ: Hãy sắp xếp các số hữu tỉ sau đây theo thứ tự tăng dần: $\frac{1}{5},\frac{-\text{ 2}}{5},\frac{3}{7},\frac{-\text{ 1}}{3},0.$

Hướng dẫn giải

• Ta so sánh $\frac{-2}{5};$ $\frac{-1}{3}$và 0.

Có:  $\frac{-\text{2}}{5}\text{\hspace{0.05em}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}}\frac{-\text{6}}{15};$ $\frac{-\text{1}}{3}\text{ = }\frac{-\text{5}}{15}$ và $0=\frac{0}{15}.$

Vì –6 < –5 < 0 nên $\frac{-\text{6}}{15}<\frac{-\text{5}}{15}\text{ <\hspace{0.17em}}\frac{0}{15}.$

Do đó $\frac{-\text{2}}{5}<\frac{-\text{1}}{3}<0.$         (1)

• Ta so sánh $\frac{1}{5}$ với $\frac{3}{7}.$

Có: $\frac{1}{5}\text{ = }\frac{7}{35}$ và $\frac{3}{7}\text{ = }\frac{15}{35}.$

Vì 7 < 15 nên $\frac{7}{35}\text{ < }\frac{15}{35}.$

Do đó $\frac{1}{5}<\frac{3}{7}.$         (2)

Lại có số hữu tỉ dương luôn lớn hơn số hữu tỉ âm.  (3)

Từ (1), (2) và (3) ta có: $\frac{-\text{2}}{5}<\frac{-\text{1}}{3}<0<\frac{1}{5}<\frac{3}{7}.$

Vậy sắp xếp các số theo thứ tự tăng dần là: $\frac{-\text{ 2}}{5}\text{; }\frac{-\text{ 1}}{3}\text{; 0; }\frac{1}{5}\text{; }\frac{3}{7}$ .

3. Biểu diễn số hữu tỉ trên trục số

– Trên trục số, mỗi số hữu tỉ được biểu diễn bởi một điểm. Điểm biểu diễn số hữu tỉ x được gọi là điểm x.

– Với hai số hữu tỉ bất kì x, y, nếu x < y thì trên trục số nằm ngang, điểm x ở bên trái điểm y.

Ví dụ:

+ Để biểu diễn số hữu tỉ $\frac{5}{4}$ ta làm như sau:

• Chia đoạn thẳng đơn vị thành bốn phần bằng nhau, ta được đoạn thẳng mới bằng $\frac{1}{4}$ đơn vị cũ.

• Số hữu tỉ $\frac{5}{4}$ được biểu diễn bởi điểm A nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 5 đơn vị mới như trong hình dưới.

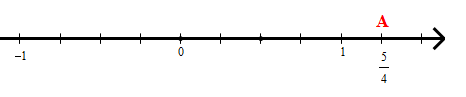
+ Để biểu diễn số hữu tỉ $\frac{4}{-3}$ trên trục số ta làm như sau:

• Viết $\frac{2}{-3}$ dưới dạng phân số với mẫu số dương $\frac{2}{-3}=\frac{-2}{3}.$

• Chia đoạn thẳng đơn vị thành ba phần bằng nhau, ta được đoạn đơn vị mới bằng $\frac{1}{3}$ đơn vị cũ.

• Số hữu tỉ $\frac{2}{-3}$ được biểu diễn bởi điểm B nằm bên trái điểm 0 và cách điểm 0 một đoạn bằng 2 đơn vị mới như hình dưới.

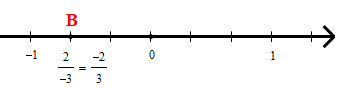
4. Số đối của một số hữu tỉ

– Hai số hữu tỉ có điểm biểu diễn trên trục số cách đều và nằm về hai phía điểm gốc O là hai số đối nhau, số này gọi là số đối của số kia.

– Số đối của số hữu tỉ x kí hiệu là −x.

Ví dụ:

$\frac{-5}{8}$ là số đối của $\frac{5}{8}$$;\frac{5}{8}$ là số đối của $\frac{-5}{8}$

0,123 là số đối của −0,123; −0,123 là số đối của 0,123.

Số đối của $1\frac{1}{2}$  (có $1\frac{1}{2}=\frac{3}{2}$) là $\frac{-3}{2}$ và ta viết là $-1\frac{1}{2}$ .

Chú ý:

– Mọi số hữu tỉ đều có một số đối.

– Số đối của số 0 là số 0.

– Với hai số hữu tỉ âm, số nào có số đối lớn hơn thì số đó nhỏ hơn.

Ví dụ: Tìm số đối của mỗi số sau: $\frac{12}{19};\frac{-1}{6};$  –2,22; 0; $2\frac{3}{4}.$

Hướng dẫn giải

Số đối của số $\frac{12}{19}$  là số $-\frac{12}{19}$

Số đối của số $\frac{-1}{6}$ là số $\frac{1}{6}$

Số đối của số –2,22 là số 2,22.

Số đối của số 0 là số 0.

Số đối của số $2\frac{3}{4}=\frac{11}{4}$là số $\frac{-11}{4}$ta viết là $-2\frac{3}{4}.$