Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài 1: Tập hợp các số hữu tỉ thẳng chi tiết sách Toán 7 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Bài 1: Tập hợp các số hữu tỉ
Video giải Toán 7 Bài 1: Tập hợp các số hữu tỉ - Chân trời sáng tạo
1. Số hữu tỉ
HĐ 1 trang 6 Toán lớp 7: Cho các số . Với mỗi số, hãy viết một phân số bằng số đã cho.
Phương pháp giải:
- Đối với số nguyên:
- Đối với hỗn số dương:
Lời giải:
Ta có: ; ; .
Chú ý: Ta cũng có thể viết các số trên bằng các phân số khác.
Thực hành 1 trang 6 Toán lớp 7: Vì sao các số là các số hữu tỉ?
Phương pháp giải:
Sử dụng định nghĩa: Số hữu tỉ là các số viết được dưới dạng phân số với
Lời giải:
Các số là các số hữu tỉ vì:
2. Thứ tự trong tập hợp số hữu tỉ
HĐ 2 trang 6 Toán lớp 7: a) So sánh hai phân số và .
b) Trong mỗi trường hợp sau, nhiệt độ nào cao hơn?
i) và ii) và .
Phương pháp giải:
a) Để so sánh hai phân số có cùng mẫu dương ta so sánh hai tử số, tử số nào lớn hơn thì phân số đó lớn hơn.
b) Số thập phân âm luôn nhỏ hơn .
Để so sánh hai số nguyên âm ta so sánh hai phần tự nhiên của chúng, số nào có phần tự nhiên lớn hơn thì số đó nhỏ hơn.
Lời giải:
a) Ta có: nên hay .
b) Ta có:
Do nên .
Thực hành 2 trang 7 Toán lớp 7: Cho các số hữu tỉ:
a) So sánh với ; với .
b) Trong các số hữu tỉ đã cho, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?
Phương pháp giải:
a) Đưa các số hữu tỉ về dạng phân số có mẫu dương rồi so sánh.
b) So sánh các số hữu tỉ đã cho với số rồi rút ra kết luận.
Lời giải:
a) +) Ta có: .
Do nên .
+) Ta có: . Nên .
b) Các số hữ tỉ dương là: .
Các số hữu tỉ âm là:
Do nên số không là số hữu tỉ dương cũng không là số hữu tỉ âm là: .
3. Biểu diễn số hữu tỉ trên trục số
HĐ 3 trang 7 Toán lớp 7: Quan sát Hình 2. Các điểm A, B, C biểu diễn các số hữu tỉ nào?
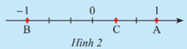
Phương pháp giải:
Quan sát Hình 2 và trả lời câu hỏi.
Lời giải:
Các điểm A, B, C biểu diễn lần lượt các số hữu tỉ:
Thực hành 3 trang 8 Toán lớp 7: a) Các điểm M, N, P trong Hình 6 biểu diễn các số hữu tỉ nào?
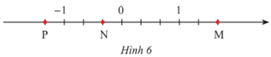
b) Biểu diễn các số hữu tỉ sau trên trục số:
Phương pháp giải:
a) Quan sát trục số và trả lời câu hỏi
b) Các số hữu tỉ âm được biểu diễn bên trái số 0, các số hữu tỉ dương được biểu diễn bên phải số 0.
Lời giải:
a) Các điểm M, N, Q biểu diễn lần lượt các số hữu tỉ:.
b)

4. Số đối của một số hữu tỉ
HĐ 4 trang 8 Toán lớp 7: Em có nhận xét gì về vị trí điểm và trên trục số (Hình 7) so với điểm 0?
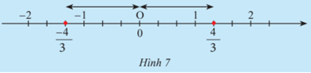
Phương pháp giải:
Nhận xét về khoảng cách từ hai điểm trên đến điểm 0.
Lời giải:
Hai điểm và cách đều và nằm về hai phía so với điểm 0.
Phương pháp giải:
Số hữu tỉ âm nào có phần số dương lớn hơn thì bé hơn.
Lời giải:
Do nên . Vì vậy phát biểu của bạn Hồng là sai.
Bài tập
Bài 1 trang 9 Toán lớp 7: Thay ? bằng kí hiệu thích hợp

Phương pháp giải:
Lời giải:
Bài 2 trang 9 Toán lớp 7: a) Trong các số sau, những phân số nào biểu diễn số hữu tỉ ?
b) Tìm số đối của mỗi số sau:
Phương pháp giải:
- Rút gọn những phân số đã cho
- Chọn những phân số bằng
Lời giải:
a) Ta có:
Vậy những phân số nào biểu diễn số hữu tỉ là:
b) Số đối của các số lần lượt là: .
Bài 3 trang 9 Toán lớp 7: a) Các điểm x, y, z trong Hình 8 biểu diễn số hữu tỉ nào?

b) Biểu diễn các số hữu tỉ trên trục số.
Phương pháp giải:
a) Quan sát Hình 8 và trả lời câu hỏi.
b) Đưa các số về dạng phân số rồi biểu diễn trên trục số.
Lời giải:
a) Các điểm x, y, z trong Hình 8 biểu diễn lần lượt các số hữu tỉ:
b) Ta có:
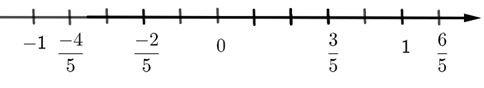
b) Hãy sắp xếp các số trên theo thứ tự từ nhỏ đến lớn.
Phương pháp giải:
a) So sánh các số đã cho với 0 và kết luận.
b) So sánh các số rồi sắp xếp các số theo thứ tự từ nhỏ đến lớn
Lời giải:
a) Các số hữu tỉ dương là:
Các số hữu tỉ âm là:
Số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm là .
b) Ta có:
Vì 0,32 < 0,8 < 2 nên -0,32 > -0,8 > -2 hay :
Mà nên
Các số theo thứ tự từ nhỏ đến lớn là:
Chú ý:
Bài 5 trang 10 Toán lớp 7: So sánh các cặp số hữu tỉ sau:
a) và b) và ;
c) và d) và .
Phương pháp giải:
- Quy đồng hoặc rút gọn để đưa các phân số về cùng mẫu.
- So sánh các phân số cùng mẫu.
Lời giải:
a) Ta có: và
Do .
b) Ta có: . Vậy =.
c) Ta có:
Do nên > .
d) Ta có: .
.
Bài 6 trang 10 Toán lớp 7: So sánh các cặp số hữu tỉ sau:
a) và ; b) và ; c) và .
Phương pháp giải:
Lời giải:
a) Ta có và nên <.
b) Ta có: và nên > .
c) Ta có: và .

a) Những rãnh đại dương nào có độ cao cao hơn rãnh Puerto Rico? Giải thích.
b) Rãnh đại dương nào có độ cao thấp nhất trong bốn rãnh trên? Giải thích.
Phương pháp giải:
a) So sánh các độ cao với rãnh Puerto Rico
b) So sánh các độ cao các rãnh đại dương và kết luận rãnh có độ cao thấp nhất.
Lời giải:
Ta có: .
Vậy ta có thứ tự các độ cao từ thấp đến cao là: Rãnh Philippine, rãnh Puerto Rico, rãnh Peru-Chile, rãnh Romanche.
a) Những rãnh có độ cao cao hơn rãnh Puerto Rico là: rãnh Peru-Chile, rãnh Romanche vì -7,7 > -8,0 > -8,6
b) Rãnh đại dương nào có độ cao thấp nhất trong bốn rãnh trên là: rãnh Philippine vì - 10,5 < - 8,6 < - 8,0 < -7,7
Lý thuyết Tập hợp các số hữu tỉ
1. Số hữu tỉ
– Số hữu tỉ là số được viết dưới dạng phân số với a, b ∈ ℤ, b ¹ 0.
– Các phân số bằng nhau biểu diễn cùng một số hữu tỉ.
– Tập hợp các số hữu tỉ được kí hiệu là ℚ.
Ví dụ:
• Các số là các số hữu tỉ.
• Các số 5; −3,4; 3 là các số hữu tỉ vì:
5 = = = …;
−3,4 = = = …;
3= = = …
– Chú ý: Mỗi số nguyên là một số hữu tỉ.
2. Thứ tự trong tập hợp các số hữu tỉ
– Với hai số hữu tỉ bất kì x, y ta luôn có: hoặc x = y hoặc x < y hoặc x > y.
– Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương.
Số hữu tỉ bé hơn 0 gọi là số hữu tỉ âm.
Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.
Ví dụ: So sánh các cặp số hữu tỉ sau:
a) −0,8 và
b) −8 và 0.
Hướng dẫn giải
a) −0,8 và
Ta có −0,8 = và .
Vì −8 < −2 và 10 > 0 nên .
Vậy – 0,8 < .
b) −8 và 0
Ta có −8= và 0 = .
Vì −26 < 0 và 3 > 0 nên .
Vậy −8 < 0.
Chú ý: Số hữu tỉ dương luôn luôn lớn hơn số hữu tỉ âm.
Ví dụ: Hãy sắp xếp các số hữu tỉ sau đây theo thứ tự tăng dần:
Hướng dẫn giải
• Ta so sánh và 0.
Có: và
Vì –6 < –5 < 0 nên
Do đó (1)
• Ta so sánh với
Có: và
Vì 7 < 15 nên
Do đó (2)
Lại có số hữu tỉ dương luôn lớn hơn số hữu tỉ âm. (3)
Từ (1), (2) và (3) ta có:
Vậy sắp xếp các số theo thứ tự tăng dần là: .
3. Biểu diễn số hữu tỉ trên trục số
– Trên trục số, mỗi số hữu tỉ được biểu diễn bởi một điểm. Điểm biểu diễn số hữu tỉ x được gọi là điểm x.
– Với hai số hữu tỉ bất kì x, y, nếu x < y thì trên trục số nằm ngang, điểm x ở bên trái điểm y.
Ví dụ:
+ Để biểu diễn số hữu tỉ ta làm như sau:
• Chia đoạn thẳng đơn vị thành bốn phần bằng nhau, ta được đoạn thẳng mới bằng đơn vị cũ.
• Số hữu tỉ được biểu diễn bởi điểm A nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 5 đơn vị mới như trong hình dưới.
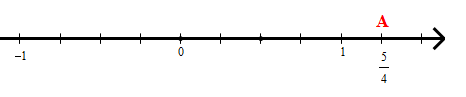
+ Để biểu diễn số hữu tỉ trên trục số ta làm như sau:
• Viết dưới dạng phân số với mẫu số dương
• Chia đoạn thẳng đơn vị thành ba phần bằng nhau, ta được đoạn đơn vị mới bằng đơn vị cũ.
• Số hữu tỉ được biểu diễn bởi điểm B nằm bên trái điểm 0 và cách điểm 0 một đoạn bằng 2 đơn vị mới như hình dưới.
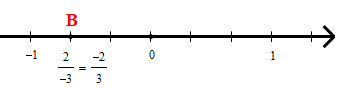
4. Số đối của một số hữu tỉ
– Hai số hữu tỉ có điểm biểu diễn trên trục số cách đều và nằm về hai phía điểm gốc O là hai số đối nhau, số này gọi là số đối của số kia.
– Số đối của số hữu tỉ x kí hiệu là −x.
Ví dụ:
là số đối của là số đối của
0,123 là số đối của −0,123; −0,123 là số đối của 0,123.
Số đối của (có ) là và ta viết là .
Chú ý:
– Mọi số hữu tỉ đều có một số đối.
– Số đối của số 0 là số 0.
– Với hai số hữu tỉ âm, số nào có số đối lớn hơn thì số đó nhỏ hơn.
Ví dụ: Tìm số đối của mỗi số sau: –2,22; 0;
Hướng dẫn giải
Số đối của số là số
Số đối của số là số
Số đối của số –2,22 là số 2,22.
Số đối của số 0 là số 0.
Số đối của số là số ta viết là
Xem thêm các bài giải SGK Toán lớp 7 Chân trời sáng tạo hay, chi tiết:
Bài 2: Các phép tính với số hữu tỉ
Bài 3: Lũy thừa của một số hữu tỉ
Bài 4: Quy tắc dấu ngoặc và quy tắc chuyển vế
Bài 5: Hoạt động thực hành và trải nghiệm: Thực hành tính tiền điện