Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài 7: Tập hợp các số thực chi tiết sách Toán 7 Tập 1 Kết nối tri thức với cuộc sống giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Bài 7: Tập hợp các số thực
Video bài giảng Tập hợp các số thực - Kết nối tri thức
1. Khái niệm số thực và trục số thực
Luyện tập 1 trang 33 Toán lớp 7: a) Cách viết nào sau đây là đúng: ?
b) Viết số đối của các số:
Phương pháp giải:
Số hữu tỉ là số viết được dưới dạng
Số hữu tỉ và số vô tỉ được gọi chung là số thực
Số đối của số thực a là -a
Lời giải:
a) Có là số vô tỉ nên không phải là số hữu tỉ, do đó .
Số π là số vô tỉ nên ta viết .
Số 15 là số hữu tỉ nên 15 là số thực, do đó .
Do đó cách viết , là đúng và là sai.
b) Số đối của 5,08(299) là -5,08(299)
Số đối của - là

Phương pháp giải:
Quan sát trục số, tìm điểm
Nhận xét điểm biểu diễn của hai số đối nhau
Lời giải:
Điểm biểu diễn số là điểm N.
Điểm biểu diễn của hai số đối nhau là 2 điểm cách đều gốc O và nằm về 2 phía của điểm O
Phương pháp giải:
Bước 1: Vẽ tam giác vuông có hai cạnh góc vuông bằng 1 và 3. Đo độ dài của cạnh huyền
Bước 2: Vẽ trục số. Biểu diễn số - trên trục số
Lời giải:
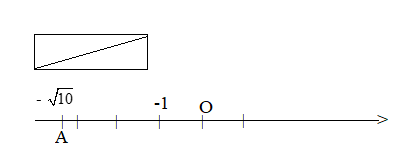
Chú ý: Các số thực âm được biểu diễn bởi các điểm nằm bên trái điểm O trên trục số.
2. Thứ tự trong tập hợp các số thực
Luyện tập 3 trang 35 Toán lớp 7: So sánh:
a) 1,313233… và 1,(32); b) và 2,36 ( có thể dùng máy tính cầm tay để tính )
Phương pháp giải:
Viết các số ở dạng số thập phân rồi so sánh các số thập phân
Lời giải:
a) Ta có: 1,(32) = 1,323232….
Quan sát chữ số ở hàng thập phân thứ 2, ta thấy 1 < 2 nên 1,313233… < 1,(32)
b) Ta có:
Quan sát chữ số ở hàng thập phân thứ nhất, ta thấy 2 < 3 nên 2,236 < 2,36
Vậy < 2,36
3. Giá trị tuyệt đối của một số thực
Phương pháp giải:
Biểu diễn các số 3 và -2 trên trục số và nhận xét
Lời giải:

Điểm 3 cách gốc O là 3 đơn vị
Điểm -2 cách gốc O là 2 đơn vị
Phương pháp giải:
Khoảng cách của 1 số nguyên đến gốc O chính bằng phần số tự nhiên của số nguyên đó.
Lời giải:
Khoảng cách của điểm -4 đến gốc O là: 4
Khoảng cách của điểm -1 đến gốc O là: 1
Khoảng cách của điểm 0 đến gốc O là: 0
Khoảng cách của điểm 1 đến gốc O là: 1
Khoảng cách của điểm 4 đến gốc O là: 4
Phương pháp giải:
Giá trị tuyệt đối của số a là khoảng cách của điểm a đến gốc O
Lời giải:
Ta có:
Câu hỏi 2 trang 36 Toán lớp 7: Minh viết: đúng hay sai?
Phương pháp giải:
Tính .
Lời giải:
Minh viết là sai vì
Chú ý:
Giá trị tuyệt đối của một số thực luôn không âm
Thử thách nhỏ trang 36 Toán lớp 7: Liệt kê các phần tử của tập hợp
Phương pháp giải:
Tìm các số nguyên x có giá trị tuyệt đối nhỏ hơn 5.
Lời giải:
Các phần tử của tập hợp A là: 0;1; -1;2; -2 ;3; -3;4; -4.
Bài tập
Phương pháp giải:
Bước 1: Tìm các số là số hữu tỉ; vô tỉ trong tập hợp A
+ Các số thập phân hữu hạn, vô hạn tuần hoàn là các số hữu tỉ
+ Các số thập phân vô hạn không tuần hoàn là các số vô tỉ
Bước 2: Mô tả tập hợp bằng cách liệt kê: Liệt kê các phần tử trong dấu { } , mỗi phần tử được liệt kê 1 lần, thứ tự tùy ý; các phần tử ngăn cách nhau bởi dấu ;
Lời giải:
Chú ý:
Số là số hữu tỉ vì = -9
Phương pháp giải:
Lời giải:
Số đối của số 7,1 là -7,1
Số đối của số -2,(61) là 2,(61)
Số đối của số 0 là 0
Số đối của số 5,14 là -5,14
Số đối của số là -
Số đối của số là -
Số đối của số
Bài 2.15 trang 36 Toán lớp 7: Các điểm A, B, C, D trong hình sau biểu diễn những số thực nào?
a)

b)

Phương pháp giải:
Đếm số vạch chia trên 1 đơn vị
Tìm số biểu diễn bởi mũi tên xanh
Lời giải:
a)

Quan sát hình ta thấy đoạn thẳng đơn vị (từ gốc O đến số 1) được chia thành 10 đoạn bằng nhau, mỗi đoạn đó lại được chia thành 2 đoạn nhỏ bằng nhau, như vậy đoạn thẳng đơn vị được chia thành 20 đoạn đơn vị mới có độ dài bằng nhau và bằng độ dài đoạn thẳng đơn vị cũ.
Điểm A nằm ở bên phải điểm O (nằm sau điểm O) và cách O một khoảng bằng 13 đoạn đơn vị mới nên điểm A biểu diễn số .
Điểm B nằm ở bên phải điểm O (nằm sau điểm O) và cách O một khoảng bằng 19 đoạn đơn vị mới nên điểm B biểu diễn số .
b)

Ta có: 4,7 – 4,6 = 0,1.
Chia đoạn thẳng 0,1 thành 20 phần bằng nhau, nên mỗi đoạn bằng
Điểm C nằm ở bên phải điểm 4,6 và cách điểm 4,6 một khoảng bằng 3 đoạn 0,005 nên điểm đó biểu diễn số 4,6 + 3.0,005 = 4,615.
Điểm D nằm ở bên phải điểm 4,6 và cách điểm 4,6 một khoảng bằng 10 đoạn 0,005 nên điểm đó biểu diễn số 4,6 + 10.0,005 = 4,65.
Bài 2.16 trang 36 Toán lớp 7: Tính:
Phương pháp giải:
Lời giải:
Chú ý:
Nếu thì
Nếu thì
Phương pháp giải:
Bước 1: Xác định dấu của từng số
Bước 2: Nếu thì
Nếu thì
Lời giải:
có dấu dương,
có dấu âm,
có dấu âm,
Bài 2.18 trang 36 Toán lớp 7: Tìm tất cả các số thực x thỏa mãn điều kiện
Phương pháp giải:
Lời giải:
Các số thực x thỏa mãn điều kiện là các số thực có khoảng cách từ số đó đến gốc tọa độ O là 2,5.
Đó là 2 số -2,5 và 2,5 nằm về 2 phía so với gốc O và cách gốc O một khoảng 2,5 đơn vị.
Chú ý: Có 2 số thực thỏa mãn giá trị tuyệt đối của nó bằng một số dương cho trước.
Lý thuyết Tập hợp các số thực
1. Khái niệm số thực và trục số thực
• Số hữu tỉ và số vô tỉ được gọi chung là số thực.
Tập hợp số thực được kí hiệu là .
Ví dụ:
+ Số là một số hữu tỉ nên cũng là một số thực.
+ Số là một số hữu tỉ nên cũng là một số thực.
+ Số là một số vô tỉ nên cũng là một số thực.
Chú ý:
• Cũng như số hữu tỉ, mỗi số thực a đều có một số đối kí hiệu là – a.
Ví dụ: Số đối của là ; số đối của là .
• Mỗi số thực đều được biểu diễn bởi một điểm trên trục số. Ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.
• Vì mỗi điểm trên trục số đều biểu diễn một số thực nên các số thực lấp đầy trục số. Người ta cũng gọi trục số là trục số thực.

• Trong tập hợp số thực cũng có các phép toán với các tính chất như trong tập số hữu tỉ.
Ví dụ: Tính giá trị của biểu thức ta làm như sau:
(Tính chất giao hoán)
(Tính chất kết hợp)
(Tổng hai số đối nhau luôn bằng 0)
(Cộng với số 0)
2. Thứ tự trong tập hợp các số thực
• Các số thực đều được viết dưới dạng số thập phân (hữu hạn hoặc vô hạn). Vì thế có thể so sánh hai số thực bằng cách viết dưới dạng số thập phân.
• Cũng như các số hữu tỉ, ta có
Với hai số thực a và b bất kì ta luôn có a = b hoặc a < b hoặc a > b.
Cho ba số thực a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).
• Trên trục số thực, nếu a < b thì điểm a nằm trước điểm b. Các điểm nằm trước gốc O biểu diễn các số âm, các điểm nằm sau gốc O biểu diễn các số dương.
• x là số âm, ta viết: x < 0; x là số dương, ta viết: x > 0.
Ví dụ:
+ So sánh và – 1,5 ta làm như sau: nên .
+ So sánh và ta làm như sau: Vì và nên .
+ Ta có nên điểm biểu diễn của trên trục số nằm giữa hai điểm A và B.

Chú ý:
• Nếu 0 < a < b thì .
Ví dụ: 0 < 3 < 5 thì .
3. Giá trị tuyệt đối của một số thực
• Với số thực a tùy ý, ta có khoảng cách từ điểm a trên trục số đến gốc O là giá trị tuyệt đối của số a, kí hiệu là .
• Hai số đối nhau thì có giá trị tuyệt đối bằng nhau.
• Giá trị tuyệt đối của 0 là 0.
• Giá trị tuyệt đối của một số dương là chính nó.
• Giá trị tuyệt đối của một số âm là số đối của nó.
Ví dụ:
+ Số 1 và –1 là hai số đối nhau và có cùng giá trị tuyệt đối là 1

+ Số nên
+ Số nên
Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 6: Số vô tỉ. Căn bậc hai số học
Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc