Với giải vở thực hành Toán 7 Bài 7: Tập hợp các số thực sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong VTH Toán 7. Mời các bạn đón xem:

Giải VTH Toán lớp 7 Bài 7: Tập hợp các số thực

Câu 1 trang 30 VTH Toán 7 Tập 1: Với mọi số thực a khác 0 đều có

A. – a là số âm;

B. – a² là số âm;

C. (– a)² là số âm;

D. (– a)³ là số âm.

Lời giải:

Đáp án đúng là B

Với mọi số thực a khác 0 thì a² > 0 nên – a² < 0. Do đó – a² là số âm.

Câu 2 trang 30 VTH Toán 7 Tập 1: Cho a là một số thực. Trên trục số nằm ngang

A. điểm biểu diễn số thực – 110,0(2) nằm bên phải điểm 0;

B. điểm biểu diễn số thực $-\frac{1}{7}$ nằm bên phải điểm biểu diễn số $-\frac{1}{5}$;

C. điểm biểu diễn số (– a) nằm bên trái điểm biểu diễn số a;

D. điểm biểu diễn số (– a) nằm bên phải điểm biểu diễn số a.

Lời giải:

Đáp án đúng là B

Ta có – 110,0(2) là số hữu tỉ âm nên – 110,0(2) < 0. Do đó điểm biểu diễn số thực – 110,0(2) nằm trước điểm 0 hay nằm bên trái điểm 0. Vì vậy A sai.

Ta có: 7 > 5 nên $\frac{1}{7}<\frac{1}{5}\Rightarrow -\frac{1}{7}>-\frac{1}{5}$. Do đó điểm biểu diễn số thực $-\frac{1}{7}$ nằm bên phải điểm biểu diễn số $-\frac{1}{5}$. Vì vậy B đúng.

Nếu a > 0 thì  – a < 0 khi đó điểm biểu diễn số (– a) nằm bên trái điểm biểu diễn số a;

Nếu a < 0 thì – a > 0 khi đó điểm biểu diễn số (– a) nằm bên phải điểm biểu diễn số a.

Do C và D sai.

Câu 3 trang 30 VTH Toán 7 Tập 1: Nếu a là số thực đã cho thì: A. |a| = a;

B. |a| = – a;

C. | – a| = – a;

D. |a|² = a².

Lời giải:

Đáp án đúng là D

Nếu a là số thực đã cho thì |a| = $\left|a\right|=\left\{\begin{array}{l}akhia\ge 0\\ -akhia<0\end{array}\right.$. Do đó A sai, B sai và C sai.

Ta có |a|² = |a|.|a| = |a.a| = |a²| = a² (vì a² ≥ 0). Do đó D đúng.

Câu 4 trang 30 VTH Toán 7 Tập 1: Nếu a < $\sqrt{2}$ và b ≥ 2 thì kết luận nào sau đây sai?

A. a < b;

B. a ≤ b;

C. – a > – b;

D. a > b.

Lời giải:

Đáp án đúng là A

Ta có: $\sqrt{2}<\sqrt{4}=2$ 

Mà a < $\sqrt{2}$ và b ≥ 2

Do đó a < b.

Câu 5 trang 30 VTH Toán 7 Tập 1: Nếu a, b ∈ ? thì A. a + b ∈ ?;

B. a.b ∈ ?;

C. a : b ∈ ?;

D. a + 1 ∈ ?.

Lời giải:

Đáp án đúng là D

Nếu a, b ∈ ? thì a + 1 ∈ ?.

Bài 1 (2.13) trang 30 VTH Toán 7 Tập 1: Xét tập hợp $A=\left\{7,1;-2,\left(61\right);0,5;14;\frac{4}{7};\sqrt{15};-\sqrt{81}\right\}.$ Bằng cách liệt kê các phần tử, hãy viết tập hợp B gồm các số hữu tỉ thuộc tập A và tập hợp C gồm các số vô tỉ thuộc tập A.

Lời giải:

Lần lượt xét các số thuộc tập hợp A, ta thấy 7,1; 0,5; 14 là những số thập phân hữu hạn và đều là số hữu tỉ. Lại có 9² = 81 nên $\sqrt{81}=9$, suy ra $-\sqrt{81}=-9$ là số thập phân hữu hạn và cũng là số hữu tỉ.

Ta lại thấy 0 – 2,(61) là số thập phân vô hạn tuần hoàn với chu kì là 61. Số $\frac{4}{7}$ là phân số tối giản mà mẫu có ước nguyên tố là 7 khác 2 và 5 nên $\frac{4}{7}$ cũng là số thập phân vô hạn tuần hoàn.

Sau cùng, vì 15 là số tự nhiên không chính phương nên $\sqrt{15}$ là số thập phân vô hạn không tuần hoàn.

Như vậy $B=\left\{7,1;-2,\left(61\right);0,5;14;\frac{4}{7};-\sqrt{81}\right\}$ và $C=\left\{\sqrt{15}\right\}$.

Bài 2 (2.14) trang 31 VTH Toán 7 Tập 1:Gọi A' là tập hợp các số đối của các số thuộc tập hợp A trong Bài tập 2.13. Liệt kê các phần tử của A'

Lời giải:

Số đối của 7,1 là –7,1.

Số đối của –2,(61) là 2,(61).

Số đối của 0 là 0.

Số đối của 0,5 là –0,5.

Số đối của 14 là – 14.

Số đối của $\frac{4}{7}$ là $-\frac{4}{7}$

Số đối của $-\sqrt{81}$ là $\sqrt{81}$

Số đối của $\sqrt{15}$ là $-\sqrt{15}$

Để viết số đối của một số dương ta chỉ cần thêm dấu trừ vào trước đố dương đã cho; để viết số đối của một số âm ta chỉ cần bỏ dấu trừ đằng trước số đó. Vì vậy

Bài 3 (2.15) trang 31 VTH Toán 7 Tập 1: Các điểm A, B, C, D trong mỗi hình sau biểu diễn số thực nào?

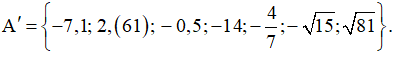
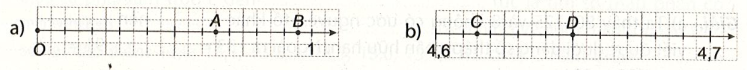
Lời giải:

a) Trong hình, các vạch chia giữa điểm 0 và điểm 1 chia đoạn nối hai điểm này thành 10 phần bằng nhau, mỗi phần có độ dài 0,1. Như vậy các vạch chia trên hình biểu diễn các số 0; 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1. Điểm A nằm chính giữa hai điểm 0,6 và 0,7 nên điểm A biểu diễn số 0,65. Tương tự điểm B nằm chính giữa hai điểm 0,9 và 1 nên điểm B biểu diễn số 0,95.

b) Đoạn nối hai điểm 4,6 và 4,7 có độ dài bằng 0,01. Các vạch chia trong hình chia đoạn này thành 10 phần bằng nhau, mỗi phần có độ dài 0,01. Các vạch chia trong hình biểu diễn các số 4,6; 4,61; 4,62; 4,63; 4,64; 4,65; 4,66; 4,67; 4,68; 4,69; 4,7. Như vậy điểm D biểu diễn số 4,65. Điểm C nằm chính giữa hai điểm 4,61 và 4,62. Do đó điểm C biểu diễn cho số 4,615.

Bài 4 (2.16) trang 31 VTH Toán 7 Tập 1: Tính: a) | -3,5 |

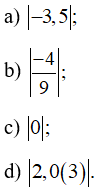
Lời giải:

Ta đã biết nếu a không âm thì |a| = a; nếu a âm thì |a| = – a. Do đó

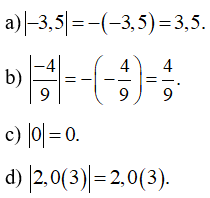
Bài 5 (2.17) trang 31 VTH Toán 7 Tập 1: Xác định dấu và giá trị tuyệt đối của các số sau:

a) a = 1,25;                 b) b = –4,1;      c) c = –1,414213562…

Lời giải:

a) a = 1,25 có dấu dương và $\left|a\right|=\left|1,25\right|=1,25.$

b) b =  –4,1 có dấu âm và $\left|b\right|=\left|-4,1\right|=4,1.$

c) c = –1,414213562… có dấu âm nên $\left|c\right|=\left|-1,\mathrm{414213562...}\right|=1,\mathrm{414213562...}$

Bài 6 (2.18) trang 32 VTH Toán 7 Tập 1: Tìm tất cả các số thực x thỏa mãn điều kiện $\left|x\right|=2,5.$

Lời giải:

Ta đã biết nếu a không âm thì |a| = a; nếu a âm thì |a| =  – a. Do đó có hai số thực x thỏa mãn điều kiện |x| = 2,5 là x = 2,5 và x = – 2,5.