Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề cực trị của hàm số, tài liệu bao gồm 62 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Chuyên đề cực trị của hàm số

Phương pháp trắc nghiệm vận dụng & vận dụng cao ứng dụng đạo hàm để khảo sát hàm số

§2. CỰC TRỊ CỦA HÀM SỐ

1. Những khái niệm cơ bản về cực trị:

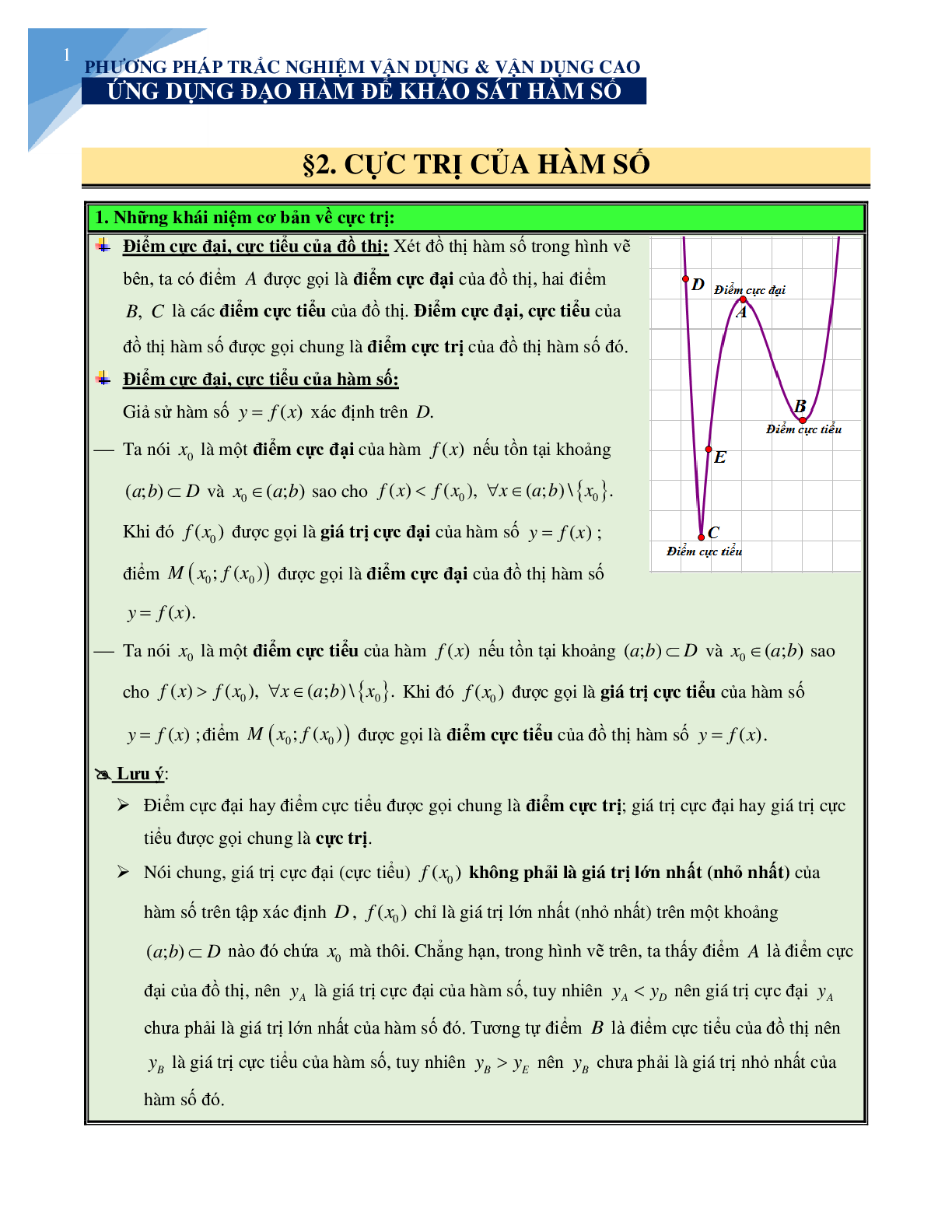
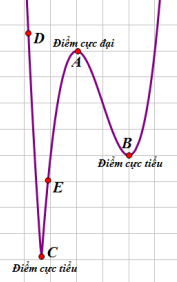
Điểm cực đại, cực tiểu của đồ thị: Xét đồ thị hàm số trong hình vẽ bên, ta có điểm A được gọi là điểm cực đại của đồ thị, hai điểm B, C là các điểm cực tiểu của đồ thị. Điểm cực đại, cực tiểu của đồ thị hàm số được gọi chung là điểm cực trị của đồ thị hàm số đó.

Điểm cực đại, cực tiểu của hàm số:

Giả sử hàm số \[y = f(x)\] xác định trên D.

Ta nói x₀ là một điểm cực đại của hàm \[y = f(x)\] nếu tồn tại khoảng (a;b) Ì D và \[{x_0} \in (a;b)\] sao cho \[f(x) < f({x_0}),\forall x \in (a;b)\backslash \{ {x_0}\} \]

Khi đó\[f({x_0})\] được gọi là giá trị cực đại của hàm số\[y = f(x)\]; điểm \[M\left( {{x_0};f({x_0})} \right)\]được gọi là điểm cực đại của đồ thị hàm số \[y = f(x)\].

Ta nói\[{x_0}\] là một điểm cực tiểu của hàm\[f(x)\] nếu tồn tại (a;b) Ì D và \[{x_0} \in (a;b)\] sao cho \[f(x) > f({x_0}),\forall x \in (a;b)\backslash \{ {x_0}\} \]. Khi đó\[f({x_0})\] được gọi là giá trị cực tiểu của hàm số \[y = f(x)\]; điểm \[M\left( {{x_0};f({x_0})} \right)\] được gọi là điểm cực tiểu của đồ thị hàm số \[y = f(x)\]

Lưu ý:

Điểm cực đại hay điểm cực tiểu được gọi chung là điểm cực trị; giá trị cực đại hay giá trị cực tiểu được gọi chung là cực trị.

Nói chung, giá trị cực đại (cực tiểu) \[f({x_0})\]không phải là giá trị lớn nhất (nhỏ nhất) của hàm số trên tập xác định D, \[f({x_0})\]chỉ là giá trị lớn nhất (nhỏ nhất) trên một khoảng (a;b) Ì D nào đó chứa x₀ mà thôi. Chẳng hạn, trong hình vẽ trên, ta thấy điểm A là điểm cực đại của đồ thị, nên y_A là giá trị cực đại của hàm số, tuy nhiên y_A < y_D nên giá trị cực đại y_A chưa phải là giá trị lớn nhất của hàm số đó. Tương tự điểm B là điểm cực tiểu của đồ thị nên y_B là giá trị cực tiểu của hàm số, tuy nhiên y_B > y_E nên y_B chưa phải là giá trị nhỏ nhất của hàm số đó.

2. Điều kiện có cực trị của hàm số:

a) Điều kiện cần: Nếu hàm số \[y = f(x)\] có đạo hàm trên \[(a;b)\]và đạt cực trị tại \[{x_0} \in (a;b)\]thì \[f'({x_0}) = 0\].

b) Điều kiện đủ:

Định lí 1: Giả sử hàm số \[y = f(x)\] liên tục trên khoảng \[(a;b)\]chứa x₀, đồng thời có đạo hàm trên khoảng\[(a;b)\]hoặc \[(a;b)\backslash \{ {x_0}\} \]. Khi đó:

Nếu \[\left\{ {\begin{array}{*{20}{c}}{f'(x) > 0,\forall x \in (a;{x_0})}\\{f'(x) < 0,\forall x \in ({x_0};b)}\end{array}} \right.\] thì hàm số\[y = f(x)\]đạt cực đại tại điểm \[x = {x_0}\].

Nếu \[\left\{ {\begin{array}{*{20}{c}}{f'(x) < 0,\forall x \in (a;{x_0})}\\{f'(x) > 0,\forall x \in ({x_0};b)}\end{array}} \right.\]thì hàm số\[y = f(x)\]đạt cực tiểu tại điểm \[x = {x_0}\].

BBT 1:Hàm số đạt cực đại tại\[x = {x_0}\].

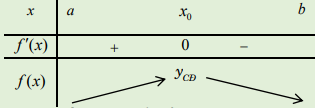
Nhận thấy:\[f'(x)\] đổi dấu từ dương sang âm khi x đi qua x₀.

BBT 2: Hàm số đạt cực tiểu tại \[x = {x_0}\].

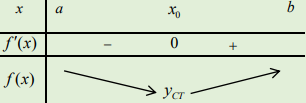
Nhận thấy:\[f'(x)\]đổi dấu từ âm sang dương khi x đi qua x₀.

Định lí 2: Giả sử hàm số\[y = f(x)\]có đạo hàm cấp hai trong khoảng \[(a;b)\]chứa x₀. Khi đó:

Nếu \[\left\{ {\begin{array}{*{20}{c}}{f'({x_0}) = 0}\\{f''({x_0}) < 0}\end{array}} \right.\] thì hàm số \[f(x)\]đạt cực đại tại\[x = {x_0}\].

Nếu \[\left\{ {\begin{array}{*{20}{c}}{f'({x_0}) = 0}\\{f''({x_0}) > 0}\end{array}} \right.\] thì hàm số \[f(x)\]đạt cực tiểu tại\[x = {x_0}\].

Dạng toán 1: Xét dấu đạo hàm để tìm cực trị của hàm số

Bài toán 1: Tính đạo hàm để tìm cực trị của hàm số \[y = f(x)\].

Phương pháp

Quy tắc I

- Tìm tập xác định.

- Tính \[y' = f'(x)\]. Tìm x khi\[f'(x) = 0\]hoặc \[f'(x)\] không xác định.

- Tính các giới hạn cần thiết.

- Lập bảng biến thiên.

- Kết luận các điểm cực trị.

Quy tắc II

- Tìm tập xác định.

- Tính \[y' = f'(x)\]. Giải phương trình\[f'(x) = 0\] để tìm các nghiệm x₁, x₂, ... (nếu có) của nó.

- Tính\[f''(x)\]và suy ra \[f''({x_1})\], \[f''({x_2})\],...

- Dựa vào dấu của \[f''({x_1})\], \[f''({x_2})\],... để kết luận.

Ghi nhớ : Quy tắc II không dùng được trong trường hợp\[f'(x) = 0\]vô nghiệm hoặc \[\left\{ {\begin{array}{*{20}{c}}{f'({x_0}) = 0}\\{f''({x_0}) = 0}\end{array}} \right.\].

Ví dụ 1. Cho hàm số \[y = {x^4} - 2{x^2} + 1\] có bao nhiêu điểm cực trị?

A. 2 .

B. 3 .

C. 1.

D. 0 .

Lời giải:

Tập xác định: D = R.

Đạo hàm:

\[\begin{array}{l}y' = 4{x^3} - 4x = 4x({x^2} - 1);\\y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0,y = 1}\\{x =  \pm 1,y = 0}\end{array}} \right.\end{array}\]

Giới hạn: \[\mathop {\lim }\limits_{x \to  \pm \infty } y =  + \infty \].

Bảng biến thiên:

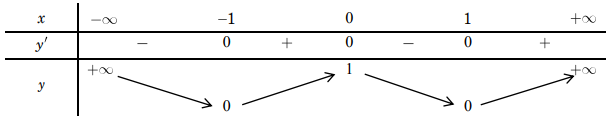
Ta thấy: Hàm số đạt cực tiểu tại \[x =  \pm 1\], giá trị cực tiểu là y_CT = 0; hàm số đạt cực đại tại x = 0, giá trị cực đại là y_CĐ = 1. Do đó hàm số có ba cực trị. Chọn B

Ví dụ 2. Tìm điểm cực đại x₀ của hàm số \[y = {x^3} - 3x + 1\].

A. x₀ = 2.

B. x₀ = 1.

C. x₀ = -1.

D. x₀ = 3.

Lời giải:

Tập xác định: D = R.

Đạo hàm: \[y' = 3{x^2} - 3;y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1 \Rightarrow y =  - 1}\\{x =  - 1 \Rightarrow y = 3}\end{array}} \right.\]

Giới hạn: \[\mathop {\lim }\limits_{x \to  + \infty } y =  + \infty ,\mathop {\lim }\limits_{x \to  - \infty } y =  - \infty .\]

Bảng biến thiên:

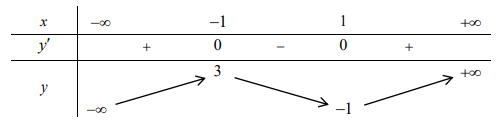
Dựa vào bảng biến thiên, ta thấy hàm số đạt cực đại tại x₀ = -1. Chọn C

Ví dụ 3. Hàm số \[y = \frac{{1 - 2x}}{{ - x + 2}}\] có bao nhiêu cực trị?

A. 3 .

B. 0 .

C. 2 .

D. 1.

Lời giải:

Tập xác định: D = R\{2}.

Ta có: \[y' = \frac{{ - 3}}{{{{( - x + 2)}^2}}} < 0,\forall x \in D\]

Giới hạn: \[\mathop {\lim }\limits_{x \to  \pm \infty } y = 2,\mathop {\lim }\limits_{x \to {2^ + }} y =  + \infty ,\mathop {\lim }\limits_{x \to {2^ - }} y =  - \infty \]

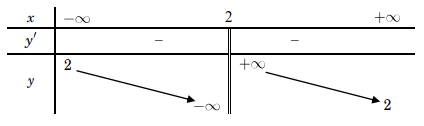
Ta thấy hàm số đã cho không có cực trị. Chọn B

Ví dụ 4. Gọi A, B là các điểm cực trị của đồ thị hàm số \[y = x + \frac{1}{x}\]. Tính khoảng cách AB .

A. \[AB = 3\sqrt 2 \]

B. \[AB = 4\]

C. \[AB = 2\sqrt 5 \]

D. \[AB = 2\sqrt 2 \]

Lời giải:

Tập xác định: D = R\{0}.

Đạo hàm: \[y' = 1 - \frac{1}{{{x^2}}} = \frac{{{x^2} - 1}}{{{x^2}}};y' = 0 \Leftrightarrow x =  \pm 1\]

Giới hạn: \[\mathop {\lim }\limits_{x \to  + \infty } y =  + \infty \], \[\mathop {\lim }\limits_{x \to  - \infty } y =  - \infty \], \[\mathop {\lim }\limits_{x \to {0^ + }} y =  + \infty ,\mathop {\lim }\limits_{x \to {0^ - }} y =  - \infty \]

Bảng biến thiên:

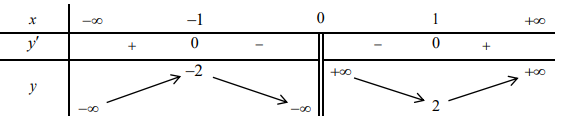
Hai điểm cực trị của đồ thị hàm số là A(-1;-2); B(1;2)

Do đó: \[AB = 2\sqrt 5 \]. Chọn C

Nhắc lại: Khoảng cách hai điểm A(x_A;y_A); B(x_B;y_B)

\[AB = \sqrt {{{({x_B} - {x_A})}^2} + {{({y_B} - {y_A})}^2}} \]

Ví dụ 5. Cho hàm số \[y = \frac{{{x^5}}}{5} + \frac{{{x^4}}}{2} - {x^3} - \frac{1}{5}\]. Mệnh đề nào sau đây là đúng ?

A. Hàm số đạt cực đại tại x = -3, đạt cực tiểu tại x =1.

B. Hàm số đạt cực tiểu tại x = -3, đạt cực đại tại x = 0.

C. Hàm số đạt cực tiểu tại x = -3 và x =1, đạt cực đại tại x = 0.

D. Hàm số đạt cực đại tại x = -3 và x =1, đạt cực tiểu tại x = 0.

Lời giải:

Tập xác định: D = R.  Đạo hàm: \[y' = {x^4} + 2{x^3} - 3{x^2} = {x^2}({x^2} + 2x - 3)\]

Xét \[y = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0 \Rightarrow y =  - \frac{1}{5}}\\{x = 1 \Rightarrow y =  - \frac{1}{2}}\\{x =  - 3 \Rightarrow y = \frac{{187}}{{10}}}\end{array}} \right.\].

Giới hạn: \[\mathop {\lim }\limits_{x \to  + \infty } y =  + \infty \], \[\mathop {\lim }\limits_{x \to  - \infty } y =  - \infty \]

Bài giảng Toán học 12 Bài 2: Cực trị của hàm số