Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Khảo sát và vẽ đồ thị hàm hữu tỉ bậc hai trên bậc nhất Toán lớp 12, tài liệu bao gồm 10 trang, tuyển chọn các bài tập Khảo sát và vẽ đồ thị hàm hữu tỉ bậc hai trên bậc nhất đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:
KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM HỮU TỈ BẬC 2/1
I. Phương pháp giải
Sơ đồ chung về khảo sát và vẽ đồ thị: Gồm 3 bước:
Bước 1: Tập xác định
- Tìm tập xác định
- Xét tính chẵn, lẻ nếu có.
Bước 2: Chiều biến thiên
- Tính các giới hạn.
- Tìm các tiệm cận đứng và tiệm cận xiên
- Tính đạo hàm cấp một, xét dấu
- Lập bảng biến thiên rồi chỉ ra khoảng đồng biến, nghịch biến và cực đại, cực tiểu.
Bước 3: Vẽ đồ thị
- Cho vài giá trị đặc biệt, giao điểm với hai trục tọa độ.
- Vẽ đúng đồ thị, lưu ý tâm đối xứng là giao điểm 2 tiệm cận đứng và tiệm cận xiên.
Các dạng đồ thị hàm hữu tỉ: \(y = \frac{{a{x^2} + bx + c}}{{a'x + b'}}\left( {a \ne 0,\,\,a' \ne 0} \right)\)
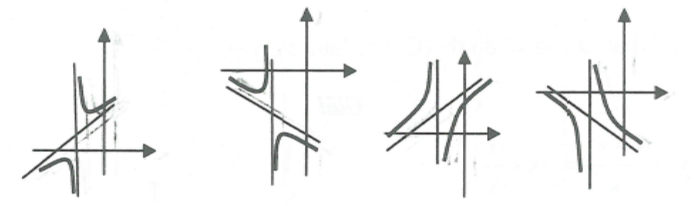
II. Ví dụ minh họa
Bài toán 1. Khảo sát sự biến thiên và vẽ đồ thị \(\left( C \right)\) của hàm số: \(y = \frac{{{x^2} + 4}}{x}.\)
Giải
● Tập xác định \(D = R\backslash \left\{ 0 \right\};\,\,y = x + \frac{4}{x}\) là hàm số lẻ.
● Sự biến thiên:
\(\mathop {\lim }\limits_{x \to {0^ - }} = - \infty ,\,\,\mathop {\lim }\limits_{x \to {0^ + }} = + \infty \) nên đường thẳng \(x = 0\) là tiệm cận đứng
\(\mathop {\lim }\limits_{x \to \pm \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to \pm \infty } \frac{4}{x}\) nên đường thẳng \(y = x\) là tiệm cận xiên.
Ta có: \(y' = 1 - \frac{4}{{{x^2}}} = \frac{{{x^2} - 4}}{{{x^2}}};\,\,y' = 0 \Leftrightarrow x = \pm 2.\)
BBT
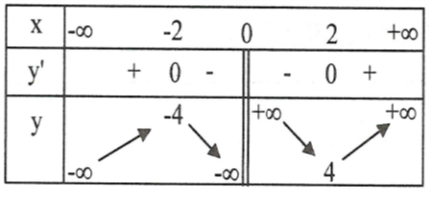
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {2; + \infty } \right)\), nghịch biến trên mỗi khoảng \(\left( { - 2;0} \right)\) và \(\left( {0;2} \right).\)
Hàm số đạt cực đại tại điểm \(x = - 2,\,\,{y_{C\~N }} = - 4\)
Hàm số đạt cực tiểu tại điểm \(x = 2,\,\,{y_{CT}} = 4.\)
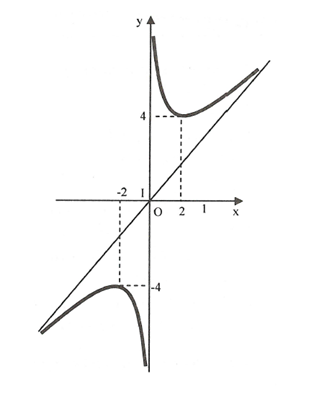
● Đồ thị:
Tâm đối xứng là giao điểm 2 tiệm cận \(O\left( {0;0} \right).\)Bài toán 2. Khảo sát và vẽ đồ thị \(\left( C \right)\) của hàm số: \(y = \frac{{1 - {x^2}}}{x}\)
Giải
Ta có \(y = \frac{{1 - {x^2}}}{x} = - x + \frac{1}{x}\)
- Tập xác định: \(D = R\backslash \left\{ 0 \right\}\). Hàm số lẻ
- Sự biến thiên: TCĐ: \(x = 0\), TCX: \(y = - x\)
\(y' = - 1 - \frac{1}{{{x^2}}} < 0,\,\,\forall x \in D\)
Bảng biến thiên
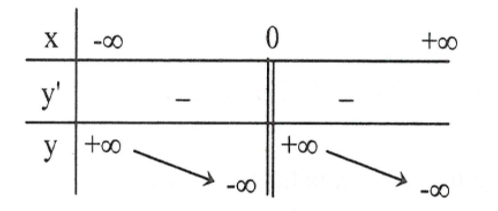
Hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).
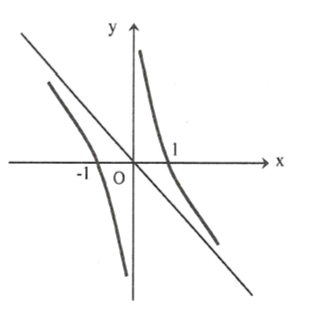
- Đồ thị: \(y = 0 \Rightarrow x = \pm 1\). Tâm đối xứng là giao điểm 2 tiệm cận \(O\left( {0;0} \right).\)
Bài toán 3. Cho hàm số \(y = \frac{{{x^2} + 2x + 5}}{{x + 1}}.\)
a) Khảo sát sự biến thiên và vẽ đồ thị \(\left( C \right)\) của hàm số
b) Tìm m để phương trình sau có hai nghiệm dương phân biệt:
\({x^2} + 2x + 5 = \left( {{m^2} + 2m + 5} \right)\left( {x + 1} \right).\)
Giải
a) \(y = \frac{{{x^2} + 2x + 5}}{{x + 1}} = x + 1 + \frac{4}{{x + 1}}\)
Tập xác định \(D = R\backslash \left\{ { - 1} \right\}.\)
Sự biến thiên: \(y' = 1 - \frac{4}{{x + 1}} = \frac{{{x^2} + 2x - 3}}{{{{\left( {x + 1} \right)}^2}}},\,\,y' = 0 \Leftrightarrow x = 1,\,\,x = - 3.\)
Ta có \[\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = - \infty ,\,\,\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = + \infty \] nên TCĐ: \(x = - 1\)
\(\mathop {\lim }\limits_{x \to \pm \infty } \left( {y - \left( {x + 1} \right)} \right) = \mathop {\lim }\limits_{x \to \pm \infty } \frac{4}{{x + 1}} = 0\) nên TCX: \(y = x + 1.\)
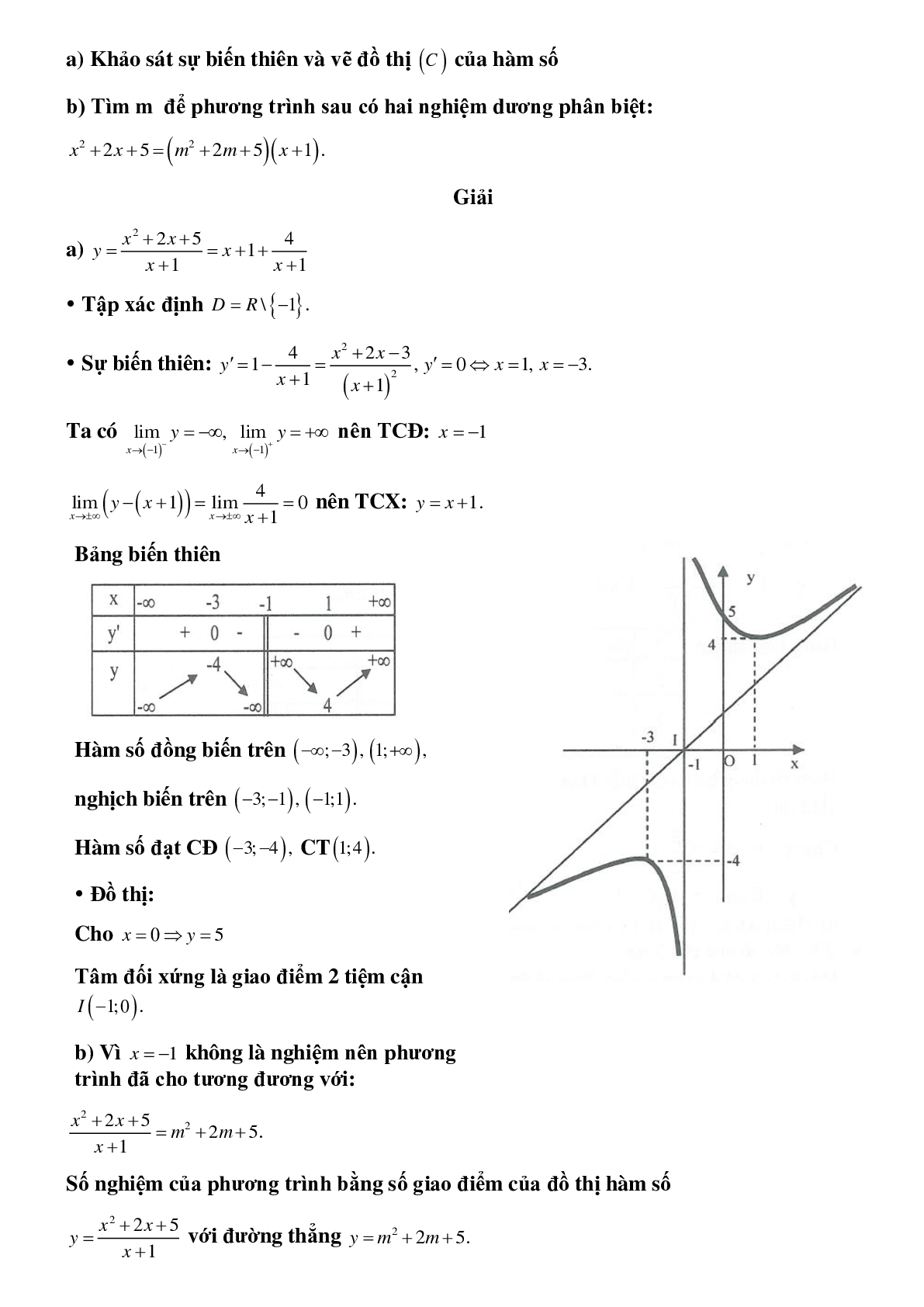
Bảng biến thiên
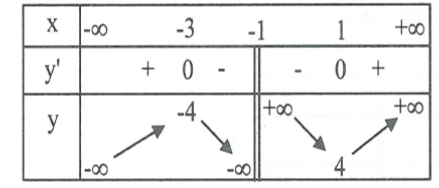
Hàm số đồng biến trên \(\left( { - \infty ; - 3} \right),\,\,\left( {1; + \infty } \right),\)
nghịch biến trên \(\left( { - 3; - 1} \right),\,\,\left( { - 1;1} \right).\)
Hàm số đạt CĐ \(\left( { - 3; - 4} \right),\) CT\(\left( {1;4} \right).\)
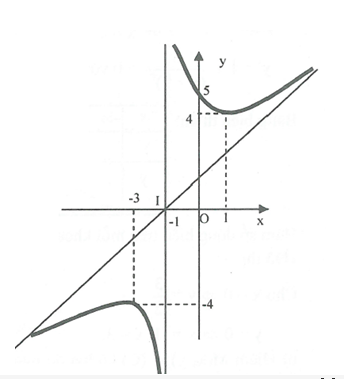
- Đồ thị:
Cho \(x = 0 \Rightarrow y = 5\)
Tâm đối xứng là giao điểm 2 tiệm cận \(I\left( { - 1;0} \right).\)
\(\frac{{{x^2} + 2x + 5}}{{x + 1}} = {m^2} + 2m + 5.\)
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số
\(y = \frac{{{x^2} + 2x + 5}}{{x + 1}}\) với đường thẳng \(y = {m^2} + 2m + 5.\)
Phương trình có hai nghiệm dương khi và chỉ khi:
\(4 < {m^2} + 2m + 5 < 5 \Leftrightarrow \left\{ \begin{array}{l}m \ne - 1\\ - 2 < m < 0\end{array} \right.\)
Bài toán 4. Cho hàm số \(y = \frac{{{x^2} - 2x - 3}}{{x - 2}}\)
a) Khảo sát sự biến thiên và vẽ đồ thị \(\left( C \right)\) của hàm số.
b) Tìm các điểm trên \(\left( C \right)\) có tọa độ là số nguyên. Chứng minh đồ thị \(\left( C \right)\) có tâm đối xứng.
Giải
a) Ta có \(y = x - \frac{3}{{x - 2}}\)
Tập xác định \(D = R\backslash \left\{ 2 \right\}.\)
Sự biến thiên: \(\mathop {\lim }\limits_{x \to {2^ - }} y = + \infty \) và \(\mathop {\lim }\limits_{x \to {2^ + }} y = - \infty \) nên TCĐ: \(x = 2.\)
\(\mathop {\lim }\limits_{x \to \pm \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to \pm \infty } \frac{3}{{x - 2}} = 0\) nên TCX: \(y = x.\)
\(y' = 1 + \frac{3}{{{{\left( {x - 2} \right)}^2}}} > 0\) với mọi \(x \ne 2\)
Bảng biến thiên:
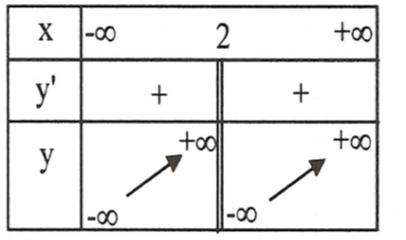
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right).\)
- Đồ thị:
Cho \(x = 0 \Rightarrow y = \frac{3}{2}\)
\(y = 0 \Rightarrow x = - 1,\,\,x = 3.\)
b) Điểm \(M\left( {x;y} \right) \in \left( C \right)\) có tọa độ nguyên khi \(x - 2\) là ước số của của 3 nên \(x - 2 = \pm 1,\,\, \pm 3.\)
Do đó \(\left( C \right)\) có 4 điểm có tọa độ nguyên:
\(\left( {1;4} \right),\,\,\left( {3;0} \right),\,\,\left( { - 1;0} \right)\) và \(\left( {5;4} \right).\)
Giao điểm 2 tiệm cận \(I\left( {2;2} \right)\) chuyển trục bằng phép tịnh tiến vectơ
\(\overrightarrow {OI} :\left\{ \begin{array}{l}x = X + 2\\y = Y + 2\end{array} \right.\)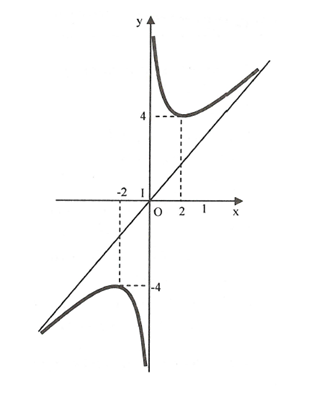
Đồ thị \(\left( C \right):Y + 2 = \left( {X + 2} \right) - \frac{3}{{\left( {X + 2} \right) - 2}} \Leftrightarrow Y = X - \frac{3}{X}\)
Vì \(Y = F\left( X \right):X - \frac{3}{X}\) là hàm số lẻ nên đồ thị \(\left( C \right)\) nhận gốc \(I\left( {2;2} \right)\) làm tâm đối xứng.
\(\frac{{{x^2} + 2x + 5}}{{x + 1}} = {m^2} + 2m + 5.\)
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
