Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề cực trị hàm ẩn, tài liệu bao gồm 17 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Chuyên đề cực trị hàm ẩn

1. Dựa vào bằng biến thiên hoặc đồ thị hàm\[f'(x)\]xác định số lần đổi dấu của\[f'(x)\]. Nếu xác định được số lần đổi dấu từ (+) sang (-) của\[f'(x)\]ta sẽ xác định được số điểm cực đại của\[f(x)\]; số lần đổi dấu từ (-) sang (+) của\[f'(x)\]ta sẽ xác định được số điểm cực tiểu của\[f(x)\].

Lỗi thường gặp: Đếm thừa điểm mà qua đó đạo hàm không đổi dấu.

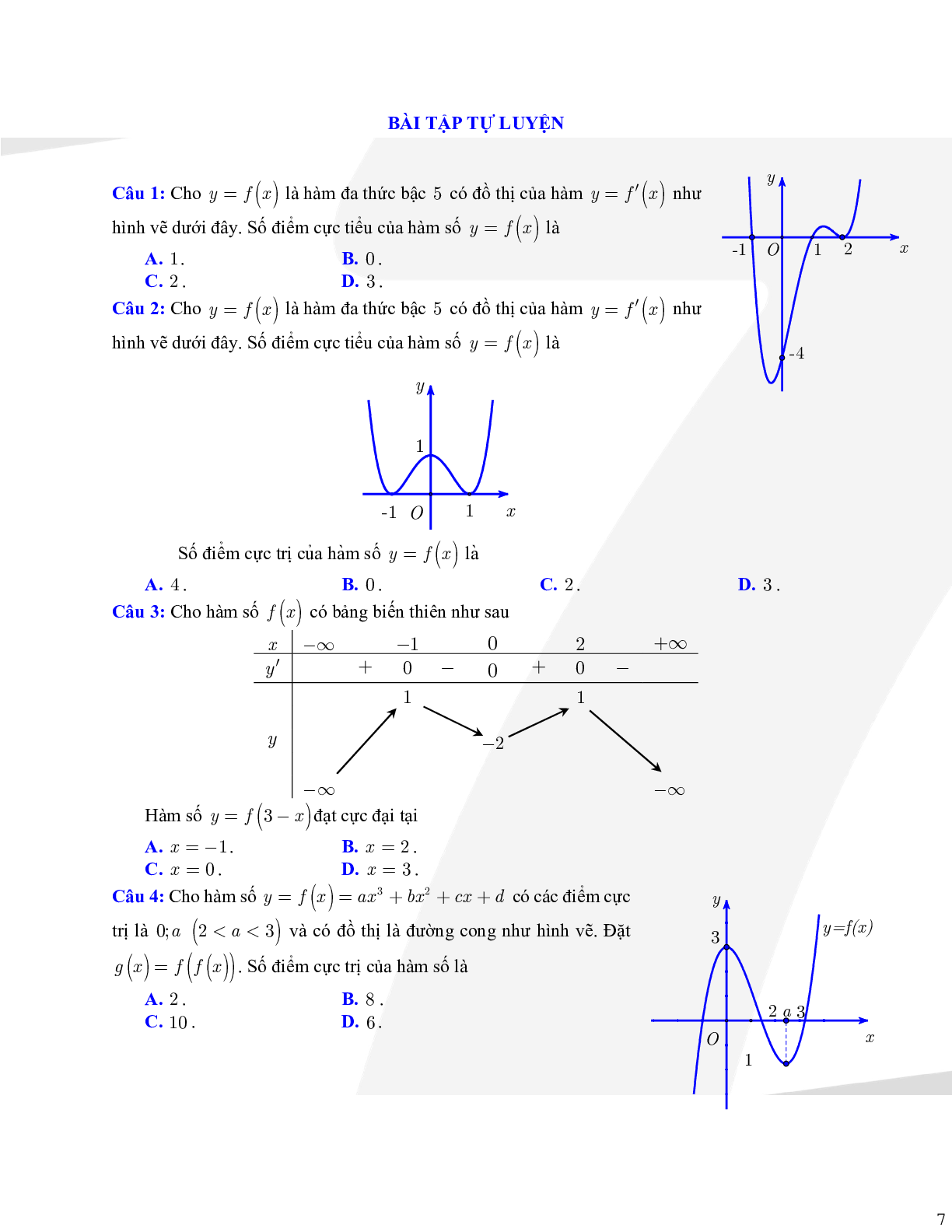
Câu 1: Cho hàm số\[f(x)\]có bảng xét dấu của\[f'(x)\]như sau:

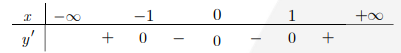
Số điểm cực trị của hàm số đã cho là

A. 0 .

B. 2 .

C. 1.

D. 3 .

Lời giải

Chọn B

Dễ thấy, \[f'(x)\]một lần đổi dấu từ (+) sang (-) và một lần đổi dấu từ (-) sang (+) nên hàm số có hai điểm cực trị.

2. Cực trị hàm \[g(x) = f\left( {u(x)} \right)\].

Để xác định số cực trị của hàm\[g(x) = f\left( {u(x)} \right)\]ta thường hướng đến việc xét dấu

\[g'(x) = u'(x)f'\left( {u(x)} \right)\].

Nếu \[g'(x)\] đổi dấu x₀ Î TXĐ của \[g(x)\] thì x₀ là điểm cực trị. Trường hợp đơn giản khi \[f(x)\],\[u(x)\] là hàm đa thức thì nghiệm đơn và nghiệm bội lẻ là các điểm cực trị của \[g(x)\].

Lỗi thường gặp: Nhầm lẫn giữa nghiệm bộ chẵn và nghiệm bội lẻ.

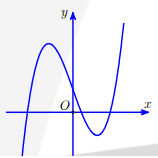
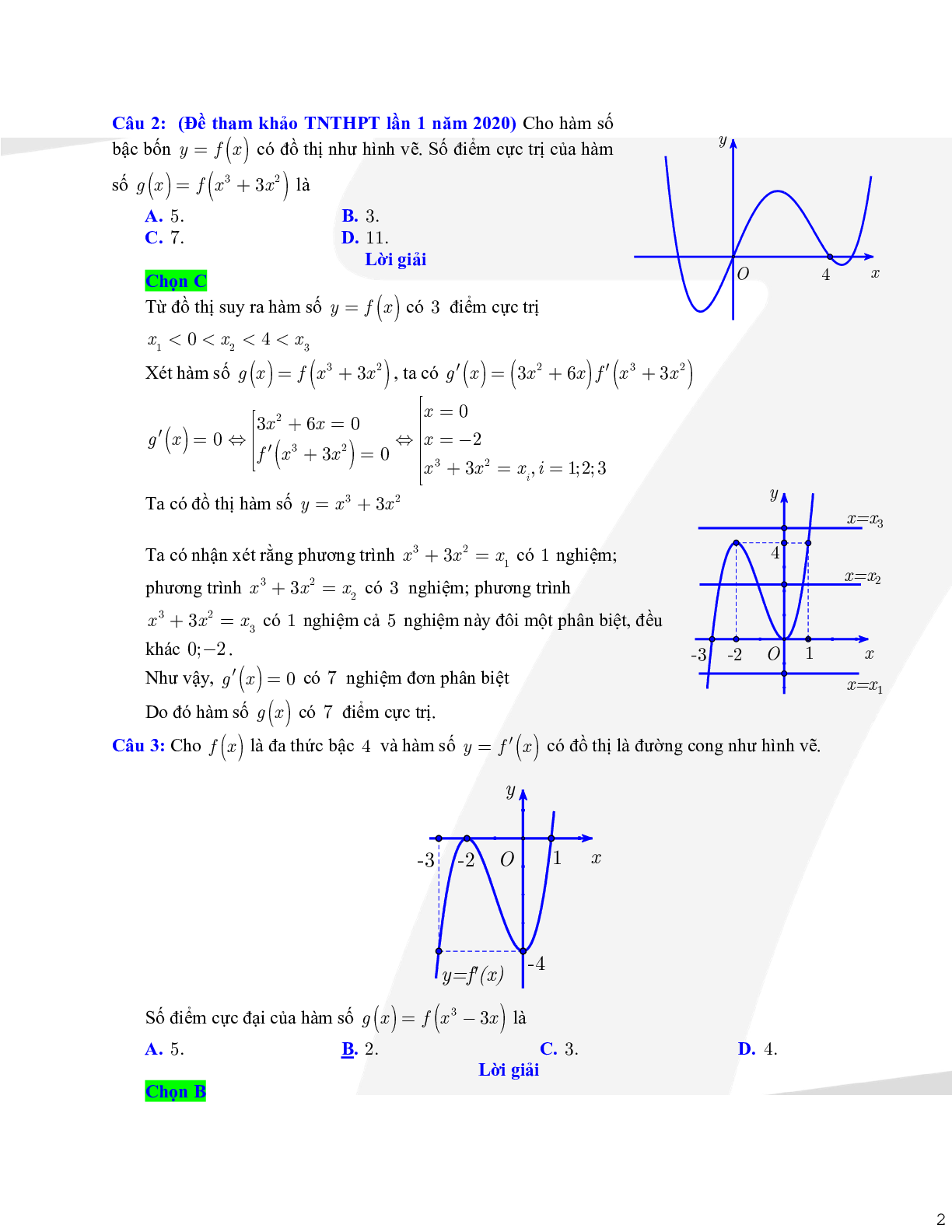
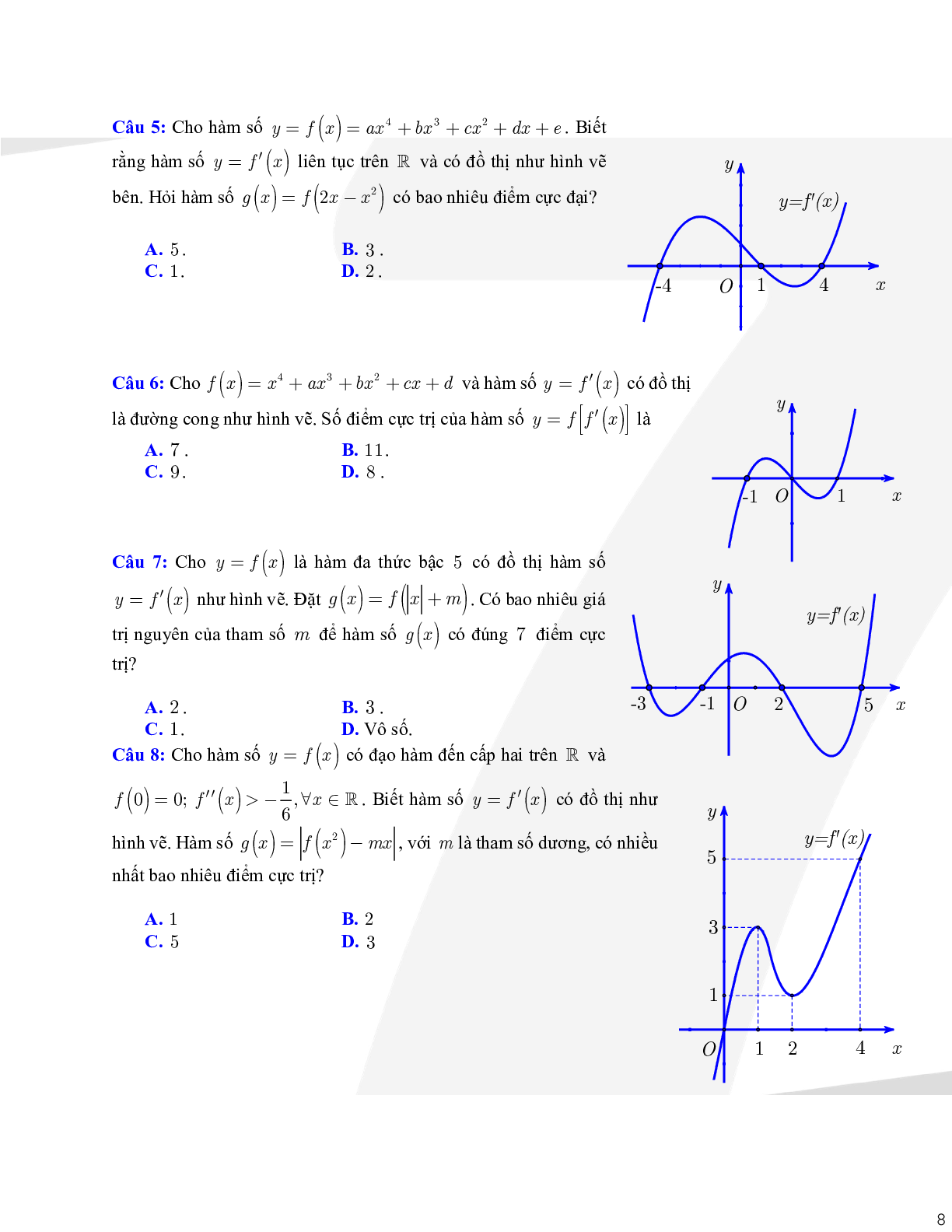
Câu 2: Cho hàm số bậc bốn\[y = f(x)\] có đồ thị như hình vẽ. Số điểm cực trị của hàm số \[g(x) = f({x^3} + 3{x^2})\] là

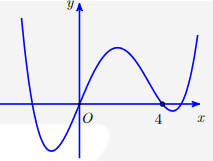
A. 5.

B. 3.

C. 7.

D. 11.

Lời giải

Chọn C

Từ đồ thị suy ra hàm số \[y = f(x)\] có 3 điểm cực trị x₁ < 0 < x₂ < 4 <x₃

Xét hàm số \[g(x) = f({x^3} + 3{x^2})\], ta có \[g'(x) = (3{x^2} + 6x)f'({x^3} + 3{x^2})\]

\[\begin{array}{l}g'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3{x^2} + 6x = 0}\\{f'({x^3} + 3{x^2}) = 0}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x =  - 2}\\{{x^3} + 3{x^2} = {x_i},i = 1;2;3}\end{array}} \right.\end{array}\]

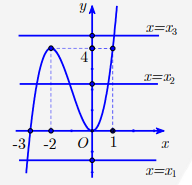
Ta có đồ thị hàm số \[y = {x^3} + 3{x^2}\]

Ta có nhận xét rằng phương trình \[{x^3} + 3{x^2} = {x_1}\] có 1 nghiệm; phương trình \[{x^3} + 3{x^2} = {x_2}\]có 3 nghiệm; phương trình \[{x^3} + 3{x^2} = {x_3}\] có 1 nghiệm cả 5 nghiệm này đôi một phân biệt, đều khác 0; -2.

Như vậy, \[g'(x) = 0\] có 7 nghiệm đơn phân biệt

Do đó hàm số \[g(x)\] có 7 điểm cực trị.

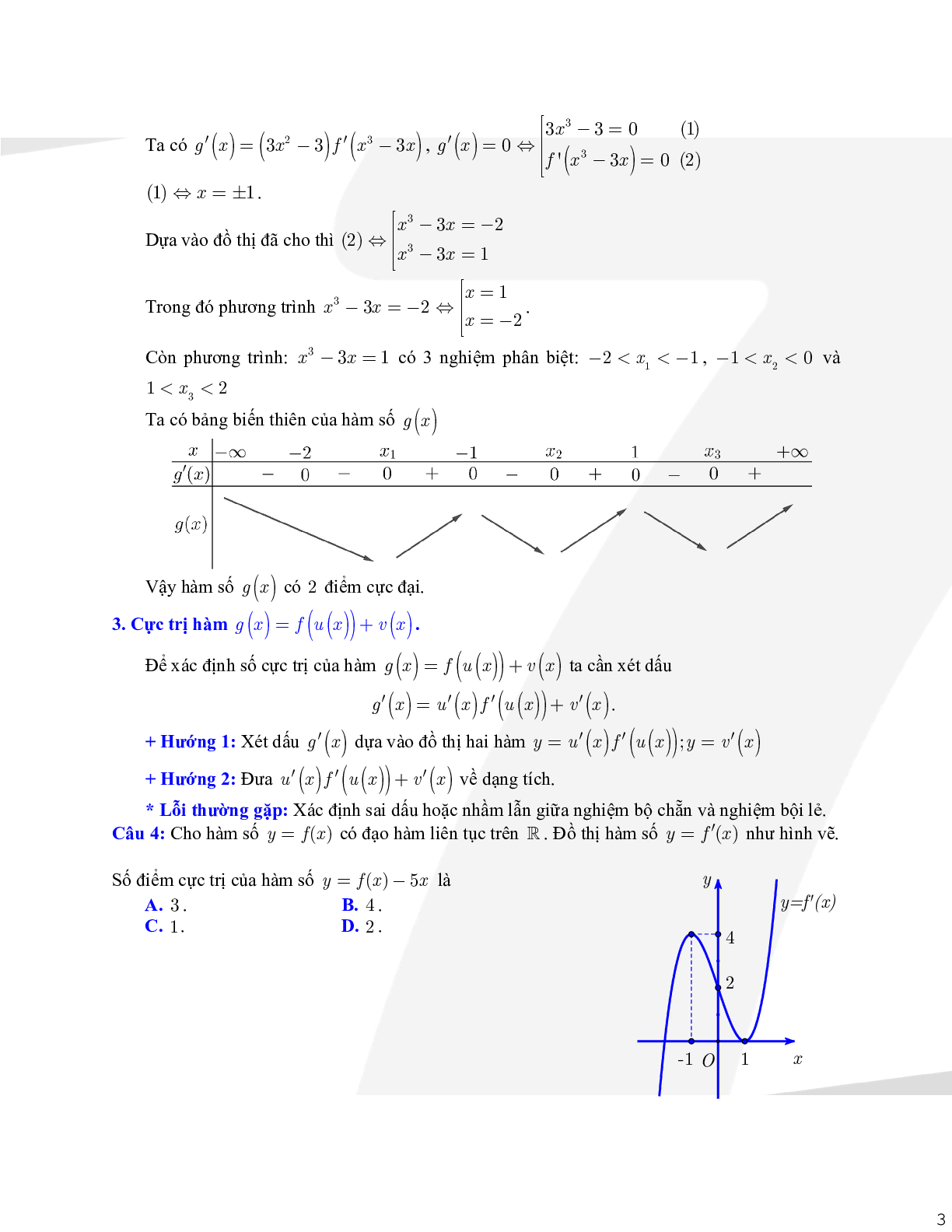
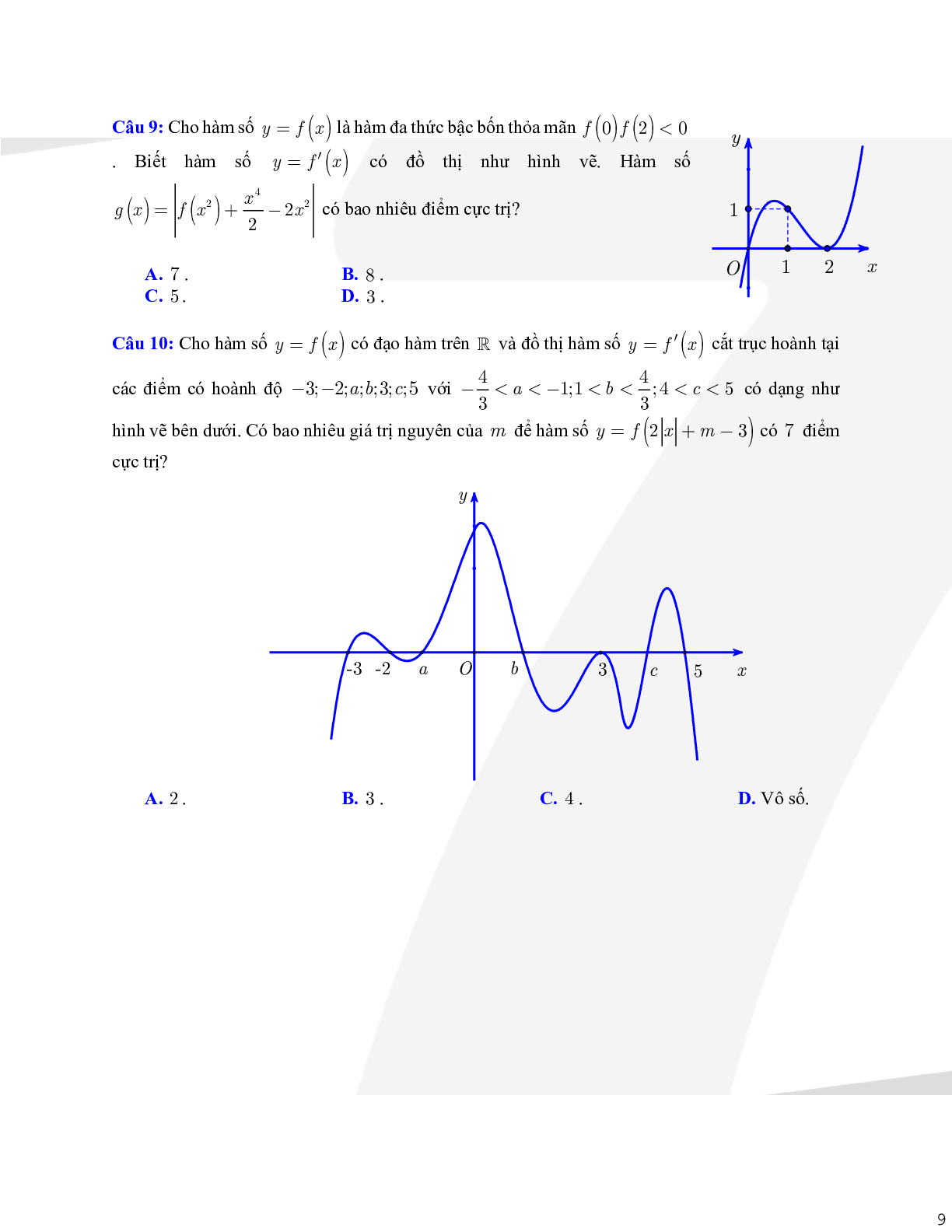
Câu 3: Cho\[f(x)\] là đa thức bậc 4 và hàm số \[y = f'(x)\] có đồ thị là đường cong như hình vẽ.

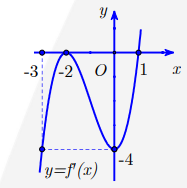
Số điểm cực đại của hàm số \[g(x) = ({x^3} - 3x)\] là

A. 5.

B. 2.

C. 3.

D. 4.

Lời giải

Chọn B

Ta có \[g'(x) = (3{x^2} - 3)f'({x^3} - 3x)\],

\[g'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3{x^2} - 3 = 0(1)}\\{f'({x^3} - 3x) = 0(2)}\end{array}} \right.\]

\[(1) \Leftrightarrow x =  \pm 1\]

Dựa vào đồ thị đã cho thì (2) Û\[\left[ {\begin{array}{*{20}{c}}{{x^3} - 3x =  - 2}\\{{x^3} - 3x = 1}\end{array}} \right.\]

Trong đó phương trình \[{x^3} - 3x =  - 2\] \[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x =  - 2}\end{array}} \right.\].

Còn phương trình: \[{x^3} - 3x = 1\] có 3 nghiệm phân biệt:

 -2 < x₁ < -1, -1 < x₂ < 0 và 1 < x₃ < 2

Ta có bảng biến thiên của hàm số \[g(x)\]

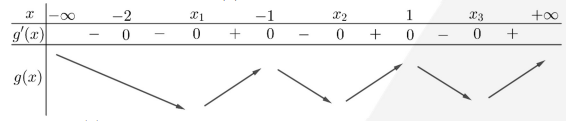
Vậy hàm số\[g(x)\] có 2 điểm cực đại.

3. Cực trị hàm \[g(x) = f\left( {u(x)} \right) + v(x)\].

Để xác định số cực trị của hàm \[g(x) = f\left( {u(x)} \right) + v(x)\] ta cần xét dấu

\[g'(x) = u'(x)f'\left( {u(x)} \right) + v'(x)\].

Hướng 1: Xét dấu \[g'(x)\] dựa vào đồ thị hai hàm \[y = u'(x)f'\left( {u(x)} \right)\]; \[y = v'(x)\]

Hướng 2: Đưa \[u'(x)f'\left( {u(x)} \right) + v'(x)\]về dạng tích.

Lỗi thường gặp: Xác định sai dấu hoặc nhầm lẫn giữa nghiệm bộ chẵn và nghiệm bội lẻ.

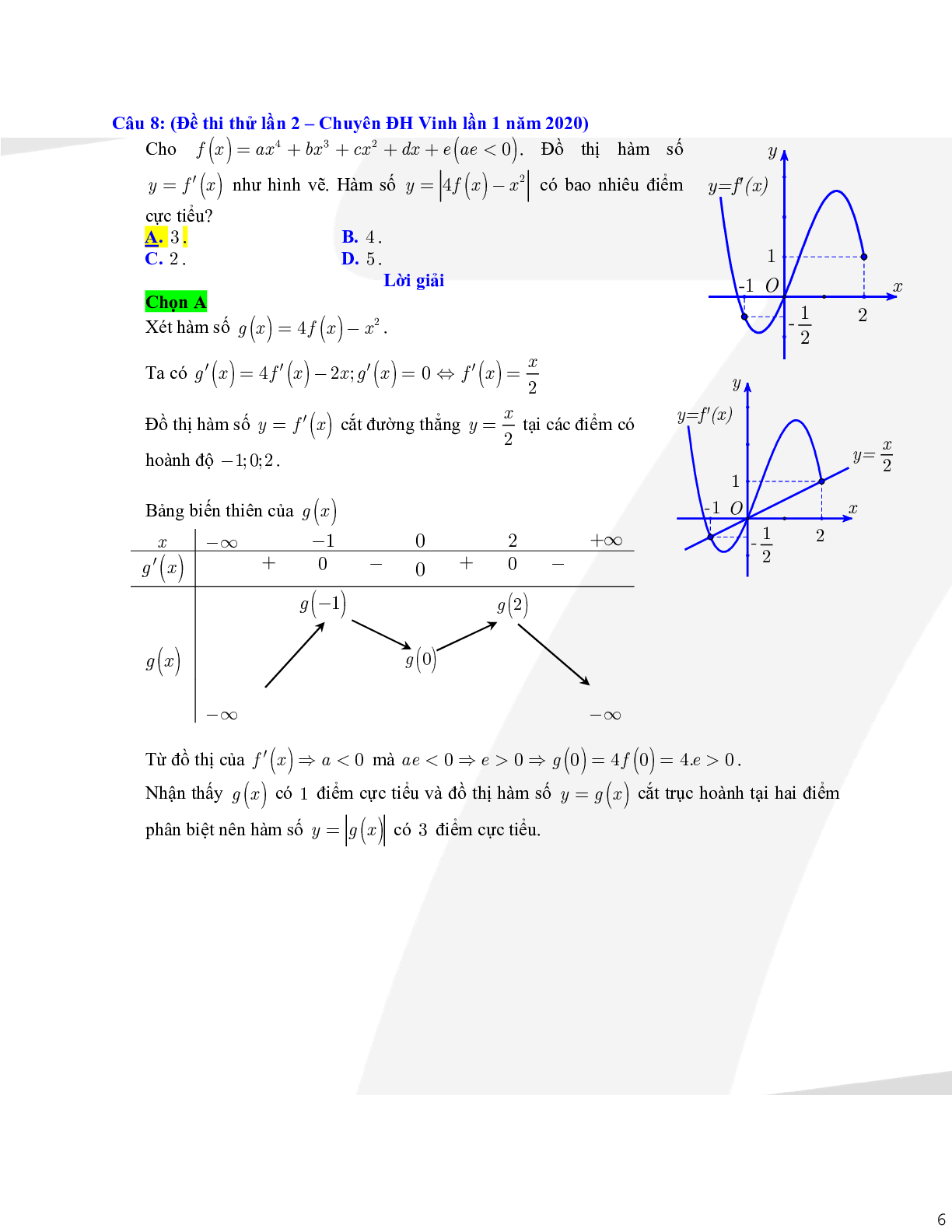
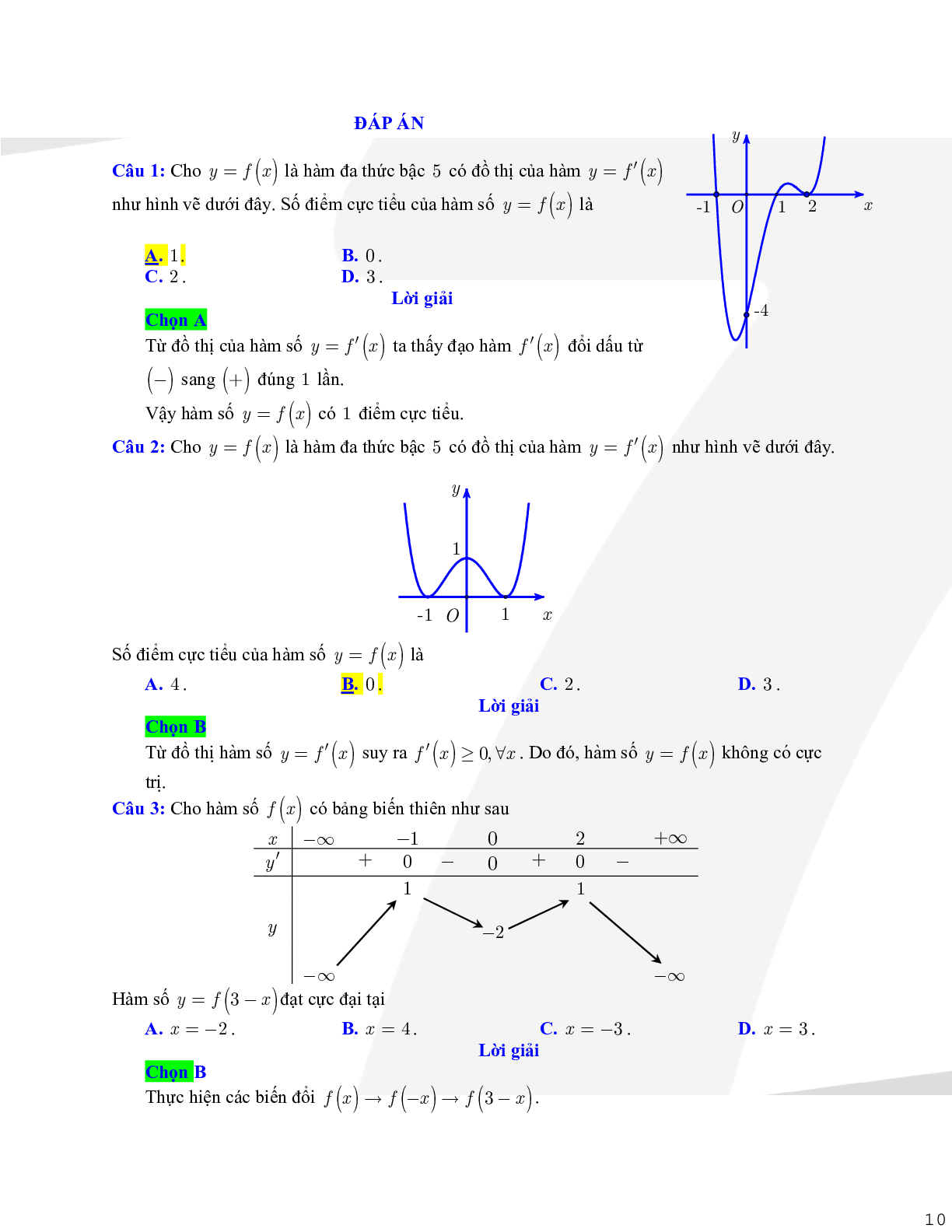
Câu 4: Cho hàm số \[y = f(x)\] có đạo hàm liên tục trên R. Đồ thị hàm số \[y = f'(x)\] như hình vẽ.

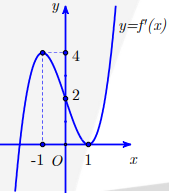
Số điểm cực trị của hàm số \[y = f(x) - 5x\] là

A. 3 .

B. 4 .

C. 1.

D. 2 .

Lời giải

Chọn C

Ta có \[y = f(x) - 5x\]. Suy ra \[y' = f'(x) - 5\].

Dựa vào đồ thị ta có \[y = f'(x)\] cắt đường thẳng y = 5 tại đúng một điểm x₀ (x₀ là nghiệm đơn của phương trình \[f'(x) = 5\]).

Vậy hàm số \[y = f(x) - 5x\] có đúng 1 điểm cực trị.

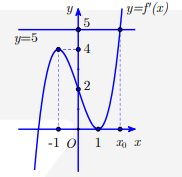
Câu 5: Cho hàm số \[y = f(x)\] là hàm đa thức bậc bốn có đồ thị hàm số \[y = f'(x)\] như hình bên vẽ. Hàm số \[g(x) = f(x) - \frac{{{x^3}}}{3} + {x^2} - x + 2\] đạt cực đại tại điểm nào?

A. x = 1 .

B. x = -1.

C. x = 0 .

D. x = 2 .

Lời giải

Chọn A

Ta có \[g(x)\] xác định trên R và \[g'(x) = f'(x) - {(x - 1)^2}\].

Số nghiệm của phương trình \[g'(x) = 0\] bằng số giao điểm của hai đồ thị \[y = f'(x)\] và parabol \[y = {(x - 1)^2}\]; \[g'(x) > 0\] khi đồ thị \[y = f'(x)\] nằm trên parabol\[y = {(x - 1)^2}\] và ngược lại.

Từ đồ thị suy ra \[g'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\\begin{array}{l}x = 2\\x = 1\end{array}\end{array}} \right.\] nhưng \[g'(x)\] chỉ đổi dấu từ dương sang âm khi qua x = 1. Do đó hàm số đạt cực đại tại x = 1.

4. Dựa vào biến đổi đồ thị

Cho hàm số \[y = f(x)\] có đồ thị (C) và a > 0 . Khi đó

Tịnh tiến (C) lên trên a đơn vị ta được đồ thị hàm số \[y = f(x) + a.\]

Tịnh tiến (C) xuống dưới a đơn vị ta được đồ thị hàm số \[y = f(x) - a.\]

Tịnh tiến (C) sang trái a đơn vị ta được đồ thị hàm số \[y = f(x + a).\]

Tịnh tiến (C) sang phải a đơn vị ta được đồ thị hàm số \[y = f(x - a).\]

Lấy đối xứng (C) qua Ox ta được đồ thị hàm số \[y =  - f(x).\]

Lấy đối xứng (C) qua Oy ta được đồ thị hàm số \[y = f( - x).\]

Lỗi thường gặp: Biến đổi đồ thị sai.

Đặc biệt khi \[f(x)\] là hàm đa thức

1) Với hàm \[y = \left| {f(x)} \right|\] (có thể mở rộng với hàm \[y = \left| {f(x) - m} \right|\])

Số điểm cực trị của đồ thị hàm số\[y = \left| {f(x)} \right|\] bằng tổng số giao điểm của đồ thị hàm số \[y = f(x)\] với Ox và số điểm cực trị không thuộc Ox của đồ thị hàm số \[y = f(x)\].

2) Với hàm \[y = f\left( {\left| x \right|} \right)\](có thể mở rộng với hàm \[y = f\left( {\left| x \right| + m} \right)\])

Số điểm cực trị của hàm số là 2k + 1 trong đó k là số điểm cực trị dương.

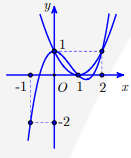
Câu 6: Cho hàm số \[y = a{x^3} + b{x^2} + cx + d\] với a ¹ 0 có đồ thị như hình vẽ. Điểm cực đại của đồ thị hàm số \[y = f\left( {4 - x} \right) + 1\] là

A. A (5;4).

B. B (3;2).

C. C (-3;4).

D. D (5;8).

Lời giải

Chọn A

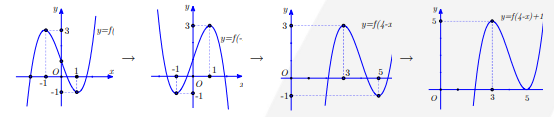
Từ đồ thị hàm số \[f(x)\] ta thực hiện các phép biến đổi

\[y = f(x) \to f( - x) \to f(4 - x) \to f(4 - x) + 1\]

Suy ra đồ thị hàm số \[f(4 - x) + 1\] có điểm cực đại là A (5;4).

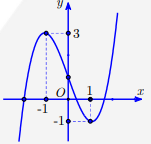
Câu 7: Cho \[y = f(x)\] là hàm đa thức bậc bốn có đồ thị hàm số \[y = f'(x)\] như hình bên vẽ. Hỏi hàm số \[y = f\left( {\left| x \right|} \right)\] có bao nhiêu điểm cực trị?

A. 5 .

B. 3 .

C. 2 .

D. 4 .

Lời giải

Chọn A

Từ đồ thị hàm số của \[f'(x)\] ta thấy \[f(x)\] có hai cực trị dương nên hàm số\[y = f\left( {\left| x \right|} \right)\]có 5 cực trị.