Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Vị trí tương đối của đường thẳng và mặt phẳng Toán lớp 12, tài liệu bao gồm 9 trang, tuyển chọn các bài tập Vị trí tương đối của đường thẳng và mặt phẳng đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có lời giải, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Tài liệu Vị trí tương đối của đường thẳng và mặt phẳng gồm các nội dung chính sau:
I. Phương pháp giải
- tóm tắt lý thuyết ngắn gọn;
- phương pháp giải chi tiết từng dạng bài tập.
II. Một số ví dụ/ Ví dụ minh họa
- gồm 15 ví dụ minh họa đa dạng của các dạng bài tập trên có lời giải chi tiết.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:
Vị trí tương đối của đường thẳng và mặt phẳng
I. Phương pháp giải
Vị trí tương đối của 2 đường thẳng:
Đường thẳng d qua và có vectơ chỉ phương .
Đường thẳng qua và có vectơ chỉ phương .
Có 4 vị trí tương đối:
- Chéo nhau: .
- Cắt nhau: và .
- Trùng nhau: .
- Song song: .
Vị trí tương đối của 1 đường thẳng và 1 mặt phẳng:
Đường thẳng d qua A và có vectơ chỉ phương .
Mặt phẳng qua và có vectơ pháp tuyến .
Có 3 vị trí tương đối:
- Cắt nhau: .
- Song song: và .
- Đường thẳng thuộc mặt phẳng: và .
Chú ý:
Đường thẳng d đi qua và có vectơ chỉ phương .
Phương trình tham số: .
Phương trình chính tắc khi : :
II. Ví dụ minh họa
Bài toán 1: Xác định vị trí tương đối giữa các cặp đường thẳng:
a) và
b) và .
Giải
a) Đường thẳng d đi qua điểm và có vectơ chỉ phương .
Đường thẳng đi qua điểm và có vectơ chỉ phương .
Ta có: nên
Vậy hai đường thẳng và chéo nhau.
b) Đường thẳng d qua điểm và có vectơ chỉ phương ; đường thẳng qua điểm và có vectơ chỉ phương .
Ta có 2 : 6 : 3 = 6 : 4 : 2
Do đó d và song song hoặc trùng nhau. Mặt khác
Vậy hai đường thẳng và trùng nhau.
Bài toán 2: Xét vị trí tương đối của các cặp đường thẳng
a) \[d:\frac{{x - 1}}{2} = \frac{{y + 5}}{1} = \frac{{z - 3}}{4}\] và \[d':\frac{{x - 6}}{3} = \frac{{y + 1}}{2} = \frac{{z + 2}}{1}\]
b) \[d:\frac{{x - 2}}{4} = \frac{y}{{ - 6}} = \frac{{z + 1}}{{ - 8}}\] và \[d':\frac{{x - 7}}{{ - 6}} = \frac{{y - 2}}{9} = \frac{z}{{12}}\]
Giải
a) d qua \[M\left( {1; - 5;\,3} \right)\] và có VTCP \[\overrightarrow u = \left( {2;\,1;\,4} \right)\].
\[d'\] qua \[M'\left( {6;\, - 1;\, - 2} \right)\] và có VTCP \[\overrightarrow {u'} = \left( {3;\,2;\,1} \right)\].
Ta có: \[\left[ {\overrightarrow u ,\,\overrightarrow {u'} \,} \right] = \left( { - 7;10;1} \right)\,;\overrightarrow {MM'} = \left( {5;4;\, - 5} \right)\] nên
\[\left[ {\overrightarrow u ,\,\overrightarrow {u'} \,} \right].\overrightarrow {MM'} = - 35 + 40 - 5 = 0\], do đó \[d\] và \[d'\]đồng phẳng.
Vì \[\left[ {\overrightarrow u ,\,\overrightarrow {u'} \,} \right] \ne 0\] nên 2 đường thẳng cắt nhau.
b) \[d\]qua \[M\left( {2;\,0;\, - 1} \right)\] và có VTCP \[\overrightarrow u = \left( {4;\, - 6;\, - 8} \right)\].
\[d'\] qua \[M'\left( {7;\,2;\,0} \right)\] và có VTCP \[\overrightarrow {u'} = \left( { - 6;\,9;\,12} \right)\].
Ta có: \[\overrightarrow {u'} = - \frac{3}{2}\overrightarrow u \] nên \[d\] , \[d'\]song song hoặc trùng nhau.
Hơn nữa \[\overrightarrow {MM'} = \left( {5;\,2;\,1} \right)\] không cùng phương với \[\overrightarrow u \], \[\overrightarrow {u'} \] nên 2 đường thẳng song song nhau.
Bài toán 3: Trong không gian với hệ tọa độ Oxyz cho 2 đường thẳng:
\[{d_1}:\left\{ {\begin{array}{*{20}{c}}{x = 2 - 2t}\\{y = 2 + t}\\{z = t}\end{array}} \right.\], \[{d_2}:\frac{{x - 1}}{{ - 2}} = \frac{y}{3} = \frac{{z - 2}}{1}\].
Chứng minh 2 đường thẳng chéo nhau.
Giải
Đường thẳng \[{d_1}\] qua \[{M_1}\left( {2;\, - 2;\,0} \right)\] và có VTCP \[\overrightarrow {{u_1}} = \left( { - 2;\,1;\,1} \right)\].
Đường thẳng \[{d_2}\] qua \[{M_2}\left( {1;\,0;\,2} \right)\] và có VTCP \[\overrightarrow {{u_2}} = \left( { - 2;\,3;\,1} \right)\].
Ta có \[\left[ {\overrightarrow {{u_1}} ,\,\overrightarrow {{u_2}} } \right] = \left( { - 2;\,0;\, - 4} \right),\,\,\overrightarrow {{M_1}{M_2}} = \left( { - 1;\, - 2;\,2} \right)\].
Nên \[\left[ {\overrightarrow {{u_1}} ,\,\overrightarrow {{u_2}} } \right].\overrightarrow {{M_1}{M_2}} = 2 + 0 - 8 = - 6 \ne 0\].
Vậy 2 đường thẳng chéo nhau.
Bài toán 4: Cho hai đường thẳng \[d:\left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = - 3 - 4t}\\{z = - 3 - 3t}\end{array}} \right.\] và \[d'\] là giao tuyến của hai mặt phẳng: \[\left( \alpha \right):x + y - z = 0\] và![]()
Chứng minh hai đường thẳng song song nhau.
Giải
Đường thẳng \[d\] đi qua điểm \[M\left( {0;\, - 3;\, - 3} \right)\] và có vectơ chỉ phương \[\overrightarrow u = \left( {1;\, - 4;\, - 3} \right)\].
Đường thẳng \[d'\] có vectơ chỉ phương \[\overrightarrow {u'} = \left( {1;\, - 4;\, - 3} \right)\].
Do đó, \[d\] và \[d'\] có cùng vectơ chỉ phương nên hai đường thẳng \[d\] và \[d'\] hoặc song song hoặc trùng nhau.
Ngoài ra vì điểm \[M\left( {0;\, - 3;\, - 3} \right)\] không nằm trên \[d'\] nên hai đường thẳng song song nhau.
Bài toán 5: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng có phương trình:
\[{d_1}:\frac{{x - 1}}{2} = \frac{{y + 2}}{{ - 3}} = \frac{{z - 5}}{4}\] và \[{d_2}:\frac{{x - 7}}{3} = \frac{{y - 2}}{3} = \frac{{z - 1}}{{ - 2}}\].
a) Chứng tỏ rằng đường thẳng đã cho cùng nằm trong một mặt phẳng.
b) Viết phương trình mặt phẳng đó.
Giải
a) \[{d_1}\] qua \[{M_1}\left( {1;\, - 2;\,5} \right)\] và có VTCP \[\overrightarrow {{u_1}} = \left( {2;\, - 3;\,4} \right)\].
\[{d_2}\] qua \[{M_2}\left( {7;\,2;\,1} \right)\] và có VTCP \[\overrightarrow {{u_2}} = \left( {3;\,2;\, - 2} \right)\].
Ta có: \[\left[ {\overrightarrow {{u_1}} ,\,\overrightarrow {{u_2}} } \right] = \left( { - 2;\,16;\,13} \right),\,\,\overrightarrow {{M_1}{M_2}} = \left( {6;\,4;\, - 4} \right)\]
Nên \[\left[ {\overrightarrow {{u_1}} ,\,\overrightarrow {{u_2}} } \right].\overrightarrow {{M_1}{M_2}} = \left( { - 2} \right)6 + 16.4 + 13\left( { - 4} \right) = 0\].
Vậy hai đường thẳng cùng nằm trong mặt phẳng.
b) Mặt phẳng \[\left( P \right)\] chứa 2 đường thẳng nên có VTPT \[\overrightarrow n = \left[ {\overrightarrow {{u_1}} ,\,\overrightarrow {{u_2}} } \right] = \left( { - 2;\,16;\,2} \right)\].
Mặt phẳng \[\left( P \right)\] đi qua \[{M_1}\] nên có phương trình:
\[ - 2\left( {x - 1} \right) + 16\left( {y + 2} \right) + 13\left( {z - 5} \right) = 0\] hay \[2{\rm{x}} - 16y - 13{\rm{z}} + 31 = 0\]
Bài toán 6: Cho hai đường thẳng \[d:\frac{{x - 1}}{2} = \frac{{y + 2}}{{ - 3}} = \frac{{z - 5}}{4}\] và \[d':\left\{ {\begin{array}{*{20}{c}}{x = 7 + 3t}\\{y = 2 + 2t}\\{z = - 1 - 3t}\end{array}} \right.\].
a) Chứng tỏ rằng hai đường thẳng cắt nhau.
b) Viết phương trình mặt phẳng chứa hai đường thẳng đó.
Giải
a) Phương trình tham số của đường thẳng d là: \[\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2{\rm{s}}}\\{y = - 2 - 3{\rm{s}}}\\{z = 5 + 4{\rm{s}}}\end{array}} \right.\].
Để tìm giao điểm của hai đường thẳng ta giải hệ: \[\left\{ {\begin{array}{*{20}{c}}{1 + 2{\rm{s}} = 7 + 3t}\\{ - 2 - 3{\rm{s}} = 2 + 2t}\\{5 + 4{\rm{s}} = - 1 - 3t}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{s = 0}\\{t = - 2}\end{array}} \right.\].
Suy ra có giao điểm \[A\left( {1;\, - 2;\,5} \right)\] nên \[d\] và \[d'\] cắt nhau.
b) Vectơ pháp tuyến của mặt phẳng \[\left( P \right)\] chứa \[d\] và \[d'\] là: \[\overrightarrow n = \left[ {\overrightarrow u ,\,\overrightarrow {u'} } \right] = \left( {1;\,18;\,13} \right)\].
Mặt phẳng \[\left( P \right)\] chứa \[d\] nên đi qua \[M\left( {1;\, - 2;\,5} \right)\].
Vậy phương trình mặt phẳng chứa \[d\] và \[d'\] là:
\[1\left( {x - 1} \right) + 18\left( {y + 2} \right) + 13\left( {z - 5} \right) = 0 \Leftrightarrow x + 18y + 13{\rm{z}} - 30 = 0\].
Bài toán 7: Cho điểm \[A\left( {1;\, - 1;\,1} \right)\] và hai đường thẳng:
\[{d_1}:\left\{ {\begin{array}{*{20}{c}}{x = t}\\{y = - 1 - 2t}\\{z = 3t}\end{array}} \right.\] và \[{d_2}:\left\{ {\begin{array}{*{20}{c}}{x = t'}\\{y = 1 + 2t'}\\{z = 4 + 5t'}\end{array}} \right.\].
Chứng minh \[\left( {{d_1}} \right),\,\left( {{d_2}} \right)\] và A cùng thuộc một mặt phẳng.
Giải
\[\left( {{d_2}} \right)\] qua \[B\left( {0;\,1;\,4} \right)\] và có VTCP \[\overrightarrow u = \left( {1;\,2;\,5} \right)\].
MP\[\left( {A,{d_2}} \right)\] qua B và có VTPT \[\overrightarrow n = \left[ {\overrightarrow u ,\,\overrightarrow {AB} } \right] = \left( { - 4;\, - 8;\, - 4} \right)\] hay \[\left( {1;\,2;\, - 1} \right)\] nên có phương trình:
\[1\left( {x - 1} \right) + 2\left( {y + 1} \right) - 1\left( {z - 1} \right) = 0 \Leftrightarrow x + 2y - z + 2 = 0\]
Ta có \[\left( {{d_1}} \right)\] qua \[M\left( {0;\, - 1;\,0} \right)\] và \[N\left( { - 1;\,1;\,3} \right)\].
Vì M, N thuộc mp \[\left( {A,{d_2}} \right)\] nên \[{d_1}\] thuộc mp \[\left( {A,{d_2}} \right)\].
Vậy A, \[\left( {{d_1}} \right),\,\left( {{d_2}} \right)\] cùng thuộc một mặt phẳng.
Bài toán 8: Trong không gian tọa độ Oxyz, cho đường thẳng \[d:\left\{ {\begin{array}{*{20}{c}}{x = 1 + 2t}\\{y = - 1 + t}\\{z = 2 - t}\end{array}} \right.\].
Gọi \[d'\] là giao tuyến của hai mặt phẳng: \[\left( \alpha \right):3y - z - 7 = 0\] và \[\left( {\alpha '} \right):3{\rm{x}} + 3y - 2{\rm{z}} - 17 = 0\].
a) Chứng minh \[d\], \[d'\] chéo nhau và vuông góc với nhau.
b) Viết phương trình mặt phẳng \[\left( P \right)\] đi qua \[d'\] và vuông góc với \[d\]. Tìm tọa độ giao điểm H của \[d\] và \[\left( P \right)\].
Giải
a) Đường thẳng \[d'\] là giao tuyến của hai mặt phẳng có vectơ pháp tuyến là \[\overrightarrow n = \left( {0;\,3;\, - 1} \right)\] và \[\overrightarrow {n'} = \left( {3;\,3;\, - 2} \right)\] nên \[d'\] có một vectơ chỉ phương là:
\[\overrightarrow {{u_{d'}}} = \left[ {\overrightarrow n ,\,\overrightarrow {n'} } \right] = \left( { - 3;\, - 3;\, - 3} \right)\] hay \[\left( {1;\,1;\,3} \right)\].
Vectơ chỉ phương \[\overrightarrow {{u_d}} \] của \[d\] là \[\overrightarrow {{u_d}} = \left( {2;\,1;\, - 1} \right)\].
Ta có: \[\overrightarrow {{u_d}} .\overrightarrow {{u_{d'}}} = 0\] nên \[d \bot d'\].
Hệ \[\left\{ {\begin{array}{*{20}{c}}{3\left( { - 1 + t} \right) - \left( {2 - t} \right) - 7 = 0}\\{3\left( {1 + 2t} \right) + 3\left( { - 1 + t} \right) - 2\left( {2 - t} \right) - 17 = 0}\end{array}} \right.\] vô nghiệm nên \[d\] và \[d'\] không có điểm chung. Vậy chúng chéo nhau.
b) Cho \[y = 0\] thì \[z = - 7\], \[x = 1\], ta có \[A\left( {1;\,0;\, - 7} \right) \in d'\]. Vì \[d \bot d'\] nên mặt phẳng đi qua A và vuông góc với \[d\] sẽ đi qua \[d'\]. Vậy phương trình mặt phẳng \[\left( P \right)\] là:
\[2\left( {x - 1} \right) + \left( {y - 0} \right) - \left( {z + 7} \right) = 0 \Leftrightarrow 2{\rm{x}} + y - z - 9 = 0\].
Tọa độ giao điểm \[H\left( {x;\,y;\,z} \right)\] của \[d\] và \[\left( P \right)\] thỏa mãn hệ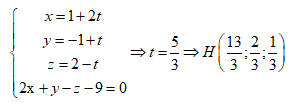
Bài toán 9: Xét vị trí tương đối của đường thẳng và mặt phẳng:
a) \[d:\frac{{x - 12}}{4} = \frac{{y - 9}}{3} = \frac{{z - 1}}{1}\] , \[\left( P \right):3{\rm{x}} + 5y - z - 2 = 0\].
b) \[d:\frac{{x + 1}}{2} = \frac{{y - 3}}{4} = \frac{z}{3}\], \[\left( P \right):3x - {\rm{3}}y + 2z - 5 = 0\]
c) \[d:\frac{{x - 13}}{8} = \frac{{y - 1}}{2} = \frac{{z - 4}}{3}\], \[\left( P \right):x + 2y - 4z + 1 = 0\].
Giải
a) Đường thẳng \[d\] có vectơ chỉ phương \[\overrightarrow u = \left( {4;\,3;\,1} \right)\].
Mặt phẳng \[\left( P \right)\] có vectơ pháp tuyến \[\overrightarrow n = \left( {3;\,5;\, - 1} \right)\].
Ta có \[\overrightarrow u .\overrightarrow n = 12 + 15 - 1 = 26 \ne 0\]. Vậy đường thẳng \[d\] cắt \[\left( P \right)\].
b) \[d\] qua \[A\left( { - 1;\,3;\,0} \right)\] và có VTCP \[\overrightarrow u = \left( {2;\,4;\,3} \right)\].
Mặt phẳng \[\left( P \right)\] có vectơ pháp tuyến \[\overrightarrow n = \left( {3;\, - 3;\,2} \right)\].
Ta có \[\overrightarrow u .\overrightarrow n = 6 - 12 + 6 = 0\] nên \[d\] song song \[\left( P \right)\] hoặc \[d\] thuộc \[\left( P \right)\].
Mà \[A \notin \left( P \right)\] nên \[d//\left( P \right)\].
c) \[d\] qua \[M\left( {13;\,1;\,4} \right)\] và có VTCP \[\overrightarrow u = \left( {8;\,2;\,3} \right)\].
Mặt phẳng \[\left( P \right)\] có vectơ pháp tuyến \[\overrightarrow n = \left( {1;\,2;\, - 4} \right)\].
Ta có \[\overrightarrow n .\overrightarrow u = 0\] mà \[M \in \left( P \right)\] nên đường thẳng \[d\] nằm trên \[\left( P \right)\].
Bài toán 10: Chứng minh đường thẳng:
a) \[d:\left\{ {\begin{array}{*{20}{c}}{x = 5t}\\{y = - \frac{7}{5} + 9t}\\{z = \frac{2}{5} + t}\end{array}} \right.\] thuộc mặt phẳng \[\left( P \right):4x - 3y + 7z - 7 = 0\].
b) \[d:\frac{{x - 1}}{2} = \frac{{y - 2}}{3} = \frac{{z - 3}}{4}\] cắt mặt phẳng \[\left( P \right):4x - y + 5z - 1 = 0\].
Giải
a) Đường thẳng \[d\] qua \[A\left( {0;\, - \frac{7}{5};\,\frac{2}{5}} \right)\] và có VTCP \[\overrightarrow u = \left( {5;\,9;\,1} \right)\].
Mặt phẳng \[\left( P \right)\] có vectơ pháp tuyến \[\overrightarrow n = \left( {4;\, - 3;\,7} \right)\].
Ta có : \[\overrightarrow n .\overrightarrow u = 0\] và \[A \in \left( P \right)\] nên \[d\] nằm trên \[\left( P \right)\].
b) Đường thẳng \[d\] có VTCP \[\overrightarrow u = \left( {2;\,3;\,4} \right)\].
Mặt phẳng \[\left( P \right)\] có vectơ pháp tuyến \[\overrightarrow n = \left( {4;\, - 1;\,5} \right)\].
Ta có \[\overrightarrow n .\overrightarrow u = 8 - 3 + 20 = 25 \ne 0\] nên \[d\] cắt mp\[\left( P \right)\].
Bài toán 11: Tìm k để đường thẳng \[d\] là giao tuyến của 2 mặt phẳng \[\left( P \right):2kx + y - z + 1 = 0\], \[\left( Q \right):x - ky + z - 1 = 0\] nằm trong mặt phẳng (Oyz).
Giải
Giao tuyến \[d\] có VTCP:
\[\overrightarrow u = \left( {\left| {\begin{array}{*{20}{c}}1&{ - 1}\\{ - k}&1\end{array}} \right|;\,\left| {\begin{array}{*{20}{c}}{ - 1}&{2k}\\1&1\end{array}} \right|;\,\left| {\begin{array}{*{20}{c}}{2k}&1\\1&{ - k}\end{array}} \right|} \right) = \left( {1 - k;\, - 1 - 2k;\, - 2{k^2} - 1} \right)\].
Mp(Oyz) có VTPT \[\overrightarrow i = \left( {1;\,0;\,0} \right)\]
Để \[d\] nằm trong mặt phẳng (Oyz) thì cần có:
\[\overrightarrow i .\overrightarrow u = 0 \Leftrightarrow \left( {1 - k} \right)1 + \left( { - 1 - 2k} \right).0 + \left( { - 2{k^2} - 1} \right).0 = 0 \Leftrightarrow k = 1\].
Thay \[k = 1\] vào phương trình của 2 mặt phẳng chứa d:
\[\left( P \right):2x + y - z + 1 = 0\], \[\left( Q \right):x - y + z - 1 = 0\].
Ta có điểm \[M\left( {0;\,0;\,1} \right)\] thuộc \[d\] và cùng thuộc mặt phẳng (Oyz) nên thỏa mãn.
Vậy để \[d\] nằm trong mặt phẳng (Oyz) thì cần và đủ là: \[k = 1\].
Bài toán 12: Trong không gian có hệ tọa độ Oxyz, cho các điểm \[A\left( {2;\,1;\,0} \right)\], \[B\left( {1;\,2;\,2} \right)\], \[C\left( {1;\,1;\,0} \right)\] và mặt phẳng \[\left( P \right):x + y + z - 20 = 0\].
Xác định tọa độ điểm D thuộc đường thẳng AB sao cho đường thẳng CD song song với mặt phẳng \[\left( P \right)\].
Giải
Ta có \[\overrightarrow {AB} = \left( { - 1;\,1;\,2} \right)\], phương trình AB: \[\left\{ {\begin{array}{*{20}{c}}{x = 2 - t}\\{y = 1 + t}\\{z = 2t}\end{array}} \right.\].
D thuộc đường thẳng AB \[ \Rightarrow D\left( {2 - t;\,1 + t;\,2t} \right) \Rightarrow \overrightarrow {C{\rm{D}}} = \left( {1 - t;\,t;\,2t} \right)\].
Vectơ pháp tuyến của mặt phẳng \[\left( P \right)\]: \[\overrightarrow n = \left( {1;\,1;\,1} \right)\].
Vì C không thuộc mặt phẳng \[\left( P \right)\] nên:
\[C{\rm{D}}//\left( P \right) \Leftrightarrow \overrightarrow n .\overrightarrow {C{\rm{D}}} = 0 \Leftrightarrow 1.\left( {1 - t} \right) + 1.t + 1.2t = 0 \Leftrightarrow t = - \frac{1}{2}\].
Vậy \[D\left( {\frac{5}{2};\,\frac{1}{2};\, - 1} \right)\].
Bài toán 13: Chứng minh các mặt phẳng: \[\left( {{P_m}} \right):\left( {2 + m} \right)x + \left( {1 + m} \right)y + \left( {1 + m} \right)z + m - 1 = 0\] luôn đi qua một đường thẳng cố định.
Giải
\[\left( {{P_m}} \right):2{\rm{x}} + y + z - 1 + m\left( {x + y + z + 1} \right) = 0\].
Mặt phẳng \[\left( {{P_m}} \right)\] đi qua các điểm \[M\left( {x;\,y;\,z} \right)\] có tọa độ không phụ thuộc m khi và chỉ khi: \[\left\{ {\begin{array}{*{20}{c}}{2{\rm{x}} + y + z - 1 = 0}\\{{\rm{x}} + y + z + 1 = 0}\end{array}} \right.\].

Bài toán 14: Chứng minh các đường thẳng \[{d_k}\] là giao tuyến của 2 mặt phẳng: \[x + k{\rm{z}} - k = 0\], \[\left( {1 - k} \right)x - ky = 0\], \[k \ne 0\] luôn nằm trên mặt phẳng cố định
Giải
Giao tuyến \[{d_k}\] chứa các điểm \[M\left( {x;\,y;\,z} \right)\] có tọa độ thỏa mãn hệ:
\[\left\{ {\begin{array}{*{20}{c}}{x + k{\rm{z}} - k = 0}\\{\left( {1 - k} \right)x - ky = 0}\end{array}} \right.;\,k \ne 0\].
Suy ra: \[x - \left( {1 - k} \right)x + k{\rm{z}} - k + ky = 0\].
\[ \Rightarrow k\left( {x + y + z - 1} \right) = 0 \Rightarrow x + y + z - 1 = 0\], vì \[k \ne 0\]
Vậy các đường thẳng \[{d_k}\] luôn luôn nằm trong mặt phẳng cố định \[\left( P \right):x + y + z - 1 = 0\]
Bài toán 15: Trong không gian Oxyz có tập hợp các mặt phẳng \[\left( {{\alpha _m}} \right)\] có phương trình là: \[m{\rm{x}} - 2\left( {m - 1} \right)y + \left( {m + 1} \right)z - 1 = 0\] và đường thẳng d có phương trình tham số:
\[\left\{ {\begin{array}{*{20}{c}}{x = 1 - 2t}\\{y = 3t}\\{z = - 2 - t}\end{array}} \right.\].
a) Chứng tỏ rằng các mặt phẳng \[\left( {{\alpha _m}} \right)\] đi qua một đường thẳng cố định \[\Delta \].
b) Chứng tỏ rằng hai đường thẳng d và \[\Delta \] chéo nhau.
Giải
a) Phương trình các mặt phẳng \[\left( {{\alpha _m}} \right)\] có thể viết thành:
\[2y + z - 1 + m\left( {x - 2y + z} \right) = 0\].
Đẳng thức này đúng với mọi m nên ta suy ra: \[\left\{ {\begin{array}{*{20}{c}}{2y + z - 1 = 0}\\{x - 2y + z = 0}\end{array}} \right.\].
Hệ phương trình này xác định một đường thẳng \[\Delta \] cố định là giao tuyến của 2 mặt phẳng \[2y + z - 1 = 0\], \[x - 2y + z = 0\].
\[\Delta \] có VTCP \[\overrightarrow n = \left[ {\overrightarrow {{n_1}} ,\,\overrightarrow {{n_2}} } \right] = \left( {4;\,1;\, - 2} \right)\] và đi qua \[B\left( { - 1;\,0;\,1} \right)\].
Vậy các mặt phẳng \[\left( {{\alpha _m}} \right)\] đi qua đường thẳng cố định \[\Delta :\frac{{x + 1}}{4} = \frac{y}{1} = \frac{{z - 1}}{{ - 2}}\].
b) d qua \[A\left( {1;\,0;\, - 2} \right)\] và có VTCP \[\overrightarrow u = \left( { - 2;\,3;\, - 1} \right)\]
Ta có \[\left[ {\overrightarrow u ,\,\overrightarrow v } \right].\overrightarrow {AB} \ne 0\] nên d và \[\Delta \] chéo nhau.