Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề tính đơn điệu của hàm số, tài liệu bao gồm 38 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Chuyên đề tính đơn điệu của hàm số

PHẦN I. CHUYÊN ĐỀ ĐẠI SỐ

Bài 1. Tính đơn điệu

A. Lý thuyết

1. Định nghĩa

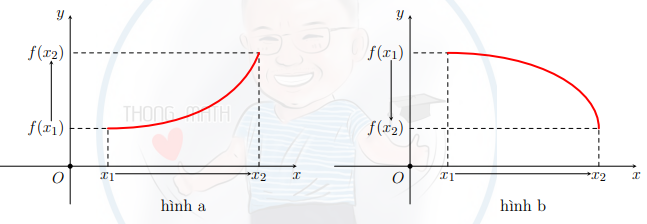
Cho hàm số \[y = f(x)\]xác định trên K, với K là một khoảng, nửa khoảng hoặc một đoạn. Hàm số\[y = f(x)\]đồng biến (tăng) trên K nếu \[\forall {x_1},{x_2} \in K,{x_1} < {x_2}\]

\[ \Rightarrow f({x_1}) < f({x_2})\] (hình a).

Hàm số\[y = f(x)\]nghịch biến (giảm) trên K nếu \[\forall {x_1},{x_2} \in K,{x_1} < {x_2}\]

\[ \Rightarrow f({x_1}) > f({x_2})\] (hình b).

2. Điều kiện cần để hàm số đơn điệu

Giả sử hàm số\[y = f(x)\] có đạo hàm trên khoảng K.

Nếu hàm số đồng biến trên khoảng K thì \[f'(x) \ge 0,\forall x \in K\].

Nếu hàm số nghịch biến trên khoảng K thì \[f'(x) \le 0,\forall x \in K\].

3. Điều kiện đủ để hàm số đơn điệu

Giả sử hàm số\[y = f(x)\]có đạo hàm trên khoảng K.

Nếu \[f'(x) > 0,\forall x \in K\] thì hàm số đồng biến trên khoảng K.

Nếu \[f'(x) < 0,\forall x \in K\] thì hàm số nghịch biến trên khoảng K.

Nếu \[f'(x) = 0,\forall x \in K\] thì hàm số không đổi trên khoảng K.

Nếu K là một đoạn hoặc nửa khoảng thì phải bổ sung giả thiết “Hàm số\[y = f(x)\] liên tục trên đoạn hoặc nửa khoảng đó ”. Chẳng hạn: Nếu hàm số\[y = f(x)\] liên tục trên đoạn [a; b] và có đọa hàm\[f'(x) > 0,\forall x \in K\] trên khoảng (a; b) thì hàm số đồng biến trên đoạn [a; b].

Nếu\[f'(x) \ge 0,\forall x \in K\] (hoặc\[f'(x) \le 0,\forall x \in K\]) và\[f'(x) = 0\] chỉ tại một số điểm hữu hạn của K thì hàm số đồng biến trên khoảng K (hoặc nghịch biến trên khoảng K).

Nếu\[f(x)\] đồng biến trên khoảng (a; b) thì \[f(a) < f(b)\].

Nếu\[f(x)\]nghịch biến trên khoảng (a; b) thì \[f(a) < f(b)\].

B. Phương pháp vận dụng

1. Lập bảng xét dấu của một biểu thức \[P(x)\]

Bước 1. Tìm nghiệm của biểu thức\[P(x)\], hoặc giá trị của x làm biểu thức\[P(x)\]không xác định.

Bước 2. Sắp xếp các giá trị của x tìm được theo thứ tự từ nhỏ đến lớn.

Bước 3. Sử dụng máy tính hoặc quy tắc xét dấu tìm dấu của\[P(x)\] trên từng khoảng của bảng xét dấu.

2. Xét tính đơn điệu của hàm số \[y = f(x)\] trên tập xác định

Bước 1. Tìm tập xác định.

Bước 2. Tính đạo hàm \[y' = f'(x)\].

Bước 3. Tìm nghiệm của \[f'(x)\]hoặc những giá trị x làm cho \[f'(x)\] không xác định.

Bước 4. Lập bảng biến thiên.

Bước 5. Kết luận.

3. Xét tính đơn điệu của hàm số \[y = f(x)\] qua Bảng biến thiên

Xét hàm số \[y = f(x)\] có đạo hàm trên (a; b), ta dựa vào bảng biến thiên để xét tính đơn điệu:

\[f'(x)\]mang dấu + (dương) thì\[f'(x)\] đồng biến trên (a; b).

Khi đó: Chiều mũi tên hướng lên trên

\[f'(x)\]mang dấu - (âm) thì\[f'(x)\]nghịch biến trên (a; b).

Khi đó: Chiều mũi tên hướng xuống dưới

Minh họa bảng biến thiên:

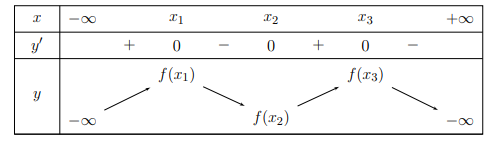
Dựa vào bảng biến thiên:

Hàm số\[y = f(x)\] đồng biến trên các khoảng (−∞; x₁) và (x₂; x₃).

Hàm số \[y = f(x)\] nghịch biến trên các khoảng (x₁; x₂) và (x₃; +∞).

4. Một số ví dụ

Ví dụ 1. Xét tính đơn điệu của hàm số sau \[y = \frac{1}{3}{x^3} - {x^2} - 3x + 1\].

Lời giải.

Tập xác định D = R.

Ta có \[y' = {x^2} - 2x - 3;y' = 0 \Leftrightarrow {x^2} - 2x - 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x =  - 1}\\{x = 3}\end{array}} \right.\].

BBT

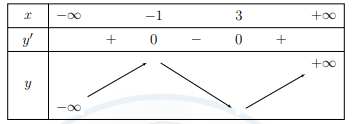
Suy ra hàm số đồng biến trên khoảng (−∞; −1) và (3; +∞); hàm số nghịch biến trên khoảng (−1; 3).

Do hàm số liên tục trên R (nghĩa là liên tục tại x = 1; x = 3) nên ta có thể kết luận như sau: Hàm số đồng biến trên (−∞; −1] và [3; +∞); hàm số nghịch biến trên [−1; 3].

Ví dụ 2. Xét tính đơn điệu của hàm số sau: \[y = {x^4} - 2{x^2} + 3\]

Lời giải.

Tập xác định D = R.

Ta có \[y' = 4{x^3} - 4x.\]

\[y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x =  \pm 1}\end{array}} \right.\]

BBT:

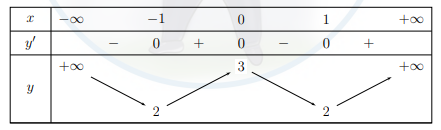
Hàm số \[y = {x^4} - 2{x^2} + 3\]nghịch biến trên (−∞; −1) nên nghịch biến trên (−2; −1).

Ví dụ 3. Xét tính đơn điệu của hàm số sau: \[y = \frac{{2x + 1}}{{x - 1}}\]

Lời giải.

Tập xác định: D = (−∞; 1) ∪ (1; +∞) ⇒ \[y' = \frac{{ - 3}}{{{{\left( {x - 1} \right)}^2}}} < 0,\forall x \ne 1\].

Hàm số nghịch biến trên từng khoảng (−∞; 1) và (1; +∞).

Ví dụ 4. Xét tính đơn điệu của hàm số sau: \[y = \sqrt {2018x - {x^2}} \]

Lời giải.

Tập xác định D = [0; 2018]; \[y' = \frac{{2018 - 2x}}{{2\sqrt {2018x - {x^2}} }};y' = 0 \Rightarrow x = 1009\]

Bảng biến thiên:

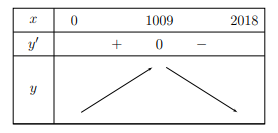
Hàm số đồng biến trên khoảng (0; 1009) và nghịch biến trên khoảng (1009; 2018).

Ví dụ 5. Xét tính đơn điệu của hàm số sau: \[y = \frac{{{x^2} - 2x + 1}}{{x - 2}}\]

Lời giải.

Tập xác định: D = R \ {2}.

Ta có \[y' = \frac{{{x^2} - 4x + 3}}{{{{\left( {x - 2} \right)}^2}}};y' = 0 \Leftrightarrow {x^2} - 4x + 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = 3}\end{array}} \right.\].

Ta có bảng biến thiên

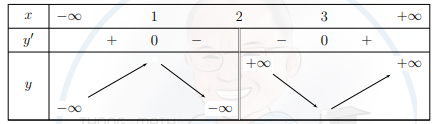
Suy ra hàm số đồng biến trên khoảng (−∞; 1) và (3; +∞).

Hàm số nghịch biến trên khoảng (1; 2) và (2; 3).

Phiếu bài tập rèn luyện số 1

Câu 1. Trong các hàm số sau, hàm số nào đồng biến trên R?

A. \[y = {x^2} + 2x - 1.\]

B. \[y = {x^4} - 2{x^2}.\]

C. \[y = {x^3} + 2x - 2019.\]

D. \[y = \frac{{2x - 1}}{{x + 3}}.\]

Câu 2. Hàm số \[y = {x^3} + 3{x^2} - 4\] nghịch biến trên khoảng nào sau đây?

A. R.

B. (−∞; −2).

C. (0; +∞).

D. (−2; 0).

Câu 3. Hàm số \[ - {x^3} - 3{x^2} + 9x + 20\] đồng biến trên các khoảng nào

A. (−3; 1).

B. (−∞; 1).

C. (−3; +∞).

D. (1; 2).

Câu 4. Cho hàm số \[y = {x^3} - 3x + 1.\] Mệnh đề nào sau đây đúng?

A. Hàm số đã cho nghịch biến trên khoảng (−2; 1).

B. Hàm số đã cho nghịch biến trên khoảng (−1; 3).

C. Hàm số đã cho đồng biến trên khoảng (−1; 1).

D. Hàm số đã cho đồng biến trên khoảng (−∞; −1) và khoảng (1; +∞).

Câu 5. Hàm số nào sau đây đồng biến trên R.

A. \[y = {x^3} - x + 2.\]

B.\[y = {x^3} + x - 1.\]

C. \[y = {x^3} - 3x + 5.\]

D. \[y = {x^4} + 4\].

Câu 6. Cho hàm số \[y = {x^4} - 8{x^2} - 4.\] Hàm số đã cho nghịch biến trên các khoảng

A. (−2; 0) và (2; +∞).

B. (−∞; −2) và (0; 2).

C. (−2; 0) và (0; 2).

D. (−∞; −2) và (2; +∞).

Câu 7. Cho hàm số\[y = {x^4} - 2{x^2}\]. Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng (−1; 1).

B. Hàm số đồng biến trên khoảng (−∞; −2).

C. Hàm số nghịch biến trên khoảng (−∞; −2).

D. Hàm số đồng biến trên khoảng (−1; 1).

Câu 8. Cho hàm số \[y = \frac{{2x - 3}}{{x + 1}}.\] Mệnh đề nào sau đây đúng?

A. Hàm số đồng biến trên tập xác định của nó.

B. Hàm số nghịch biến trên tập R.

C. Hàm số đồng biến trên (−∞; −1) và (−1; +∞).

D. Hàm số nghịch biến trên R\ {−1}.

Câu 9. Cho hàm số \[y = \frac{{x - 1}}{x}.\] Mệnh đề nào sau đây là đúng?

A. Hàm số đã cho chỉ đồng biến trên (0; +∞).

B. Hàm số đã cho chỉ đồng biến trên (−∞; 0).

C. Hàm số đã cho đồng biến trên R\ {0}.

D. Hàm số đã cho đồng biến trên mỗi khoảng xác định.

Câu 10. Cho hàm số \[y = \frac{{2x + 1}}{{x + 2}}.\] Khẳng định nào sau đây là đúng?

A. Hàm số nghịch biến trên R.

B. Hàm số đồng biến trên R.

C. Hàm số nghịch biến trên các khoảng (−∞; −2) và (−2; +∞).

D. Hàm số đồng biến trên các khoảng (−∞; −2) và (−2; +∞).