Với giải Hoạt động khám phá 4 trang 75 Toán 11 Tập 1 Chân trời sáng tạo chi tiết trong Bài 2: Giới hạn của hàm số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 2: Giới hạn của hàm số
Hoạt động khám phá 4 trang 75 Toán 11 Tập 1: Cho hàm số có đồ thị như Hình 3.
a) Tìm các giá trị còn thiếu trong bảng sau:
|
x |
10 |
100 |
1 000 |
10 000 |
100 000 |
|
y = f(x) |
0,1 |
0,01 |
? |
? |
? |
Từ đồ thị và bảng trên, nêu nhận xét về giá trị f(x) khi x càng lớn (dần tới +∞)?
b) Tìm các giá trị còn thiếu trong bảng sau:
|
x |
– 100 000 |
– 10 000 |
– 1 000 |
– 100 |
– 10 |
|
y = f(x) |
? |
? |
? |
–0,01 |
–0,1 |
Từ đồ thị và bảng trên, nêu nhận xét về giá trị f(x) khi x càng bé (dần tới – ∞)?
Lời giải:
a) Với x = 1 000 suy ra ;
Với x = 10 000 suy ra ;
Với x = 100 000 suy ra .
Từ đó ta có bảng sau:
|
x |
10 |
100 |
1 000 |
10 000 |
100 000 |
|
y = f(x) |
0,1 |
0,01 |
0,001 |
0,0001 |
0,00001 |
b) Với x = – 100 000 suy ra ;
Với x = – 10 000 suy ra ;
Với x = – 1 000 suy ra .
Từ đó ta có bảng sau:
|
x |
– 100 000 |
– 10 000 |
– 1 000 |
– 100 |
– 10 |
|
y = f(x) |
–0,00001 |
–0,0001 |
–0,001 |
–0,01 |
–0,1 |
Lý thuyết Giới hạn hữu hạn của hàm số tại vô cực
Cho hàm số xác định trên khoảng . Ta nói hàm số có giới hạn là số L khi nếu với dãy số bất kì và ta có , kí hiệu hay khi .
Cho hàm số xác định trên khoảng . Ta nói hàm số có giới hạn là số L khi nếu với dãy số bất kì và ta có , kí hiệu hay khi .
* Nhận xét:
Xem thêm các lời giải bài tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Thực hành 1 trang 72 Toán 11 Tập 1: Tìm các giới hạn sau:....
Hoạt động khám phá 2 trang 72 Toán 11 Tập 1: Cho hai hàm số y = f(x) = 2x và y = g(x) = .....
Thực hành 2 trang 73 Toán 11 Tập 1: Tìm các giới hạn sau:.....
Thực hành 3 trang 75 Toán 11 Tập 1: Cho hàm số 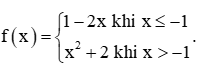
Hoạt động khám phá 4 trang 75 Toán 11 Tập 1: Cho hàm số có đồ thị như Hình 3....
Thực hành 4 trang 76 Toán 11 Tập 1: Tìm các giới hạn sau:....
Hoạt động khám phá 5 trang 77 Toán 11 Tập 1: Cho hàm số có đồ thị như Hình 4....
Thực hành 5 trang 78 Toán 11 Tập 1: Tìm các giới hạn sau....
Bài 1 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau:....
Bài 2 trang 79 Toán 11 Tập 1: Cho hàm số 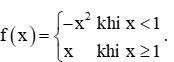
Bài 3 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau:....
Bài 4 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau:...
Xem thêm các bài giải SGK Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác: