Thực hành 3 trang 75 Toán 11 Tập 1 Chân trời sáng tạo | Giải bài tập Toán lớp 11

Thực hành 3 trang 75 Toán 11 Tập 1 Chân trời sáng tạo | Giải bài tập Toán lớp 11

Van Anh Ngày: 20-08-2024 Lớp 11

459

Với giải Thực hành 3 trang 75 Toán 11 Tập 1 Chân trời sáng tạo chi tiết trong Bài 2: Giới hạn của hàm số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 2: Giới hạn của hàm số

Thực hành 3 trang 75 Toán 11 Tập 1: Cho hàm số

Tìm các giới hạn $\lim_{x \to - 1^{+}} f (x), \lim_{x \to - 1^{-}} f (x)$ và $\lim_{x \to - 1} f (x)$ (nếu có).

Lời giải:

+) Với dãy số (x_n) bất kì, x_n ≤ – 1 và x_n → – 1. Khi đó f(x_n) = 1 – 2x_n nên limf(x_n) = lim(1 – 2x_n) = 3.

Vì vậy $\lim_{x \to - 1^{-}} f (x) = 3$ .

+) Với dãy số (x_n) bất kì, x_n > – 1 và x_n → – 1. Khi đó f(x_n) = $x_{n}^{2} + 2$ nên limf(x_n) = lim( $x_{n}^{2} + 2$ ) = 3.

Vì vậy $\lim_{x \to - 1^{+}} f (x) = 3$ .

Vì $\lim_{x \to - 1^{+}} f (x) = \lim_{x \to - 1^{-}} f (x) = 3$ nên $\lim_{x \to - 1} f (x) = 3$ .

Lý thuyết Giới hạn một phía

Cho hàm số $y = f (x)$ xác định trên khoảng $(x_{0}; b)$ .

Ta nói $y = f (x)$ có giới hạn bên phải là số L khi $x \to x_{0}$ nếu với dãy số $(x_{n})$ bất kì, $x_{0} < x_{n} < b$ và $x_{n} \to x_{0}$ ta có $f (x_{n}) \to L$ , kí hiệu $lim_{x \to {x_{0}}^{+}} f (x) = L$ .

Cho hàm số $y = f (x)$ xác định trên khoảng $(a; x_{0})$ .

Ta nói $y = f (x)$ có giới hạn bên phải là số L khi $x \to x_{0}$ nếu với dãy số $(x_{n})$ bất kì, $a < x_{n} < x_{0}$ và $x_{n} \to x_{0}$ ta có $f (x_{n}) \to L$ , kí hiệu $lim_{x \to {x_{0}}^{-}} f (x) = L$ .

*Chú ý:

$lim_{x \to x_{0}} f (x) = L \Leftrightarrow lim_{x \to {x_{0}}^{-}} f (x) = lim_{x \to {x_{0}}^{+}} f (x) = L$

$lim_{x \to {x_{0}}^{-}} f (x) \neq lim_{x \to {x_{0}}^{+}} f (x)$ thì không tồn tại $lim_{x \to x_{0}} f (x)$ .

Các phép toán về giới hạn hữu hạn của hàm số ở Mục 2 vẫn đúng khi ta thay $x \to x_{0}$ bằng $x \to {x_{0}}^{+}$ hoặc $x \to {x_{0}}^{-}$ .

Xem thêm các lời giải bài tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Hoạt động khởi động trang 71 Toán 11 Tập 1: Quan sát hình bên, cho biết hình chữ nhật OHMK thay đổi nhưng điểm M luôn nằm trên đồ thị hàm số $y = \frac{1}{x^{2}}$ (x > 0). Diện tích hình chữ nhật sẽ thay đổi như thế nào khi điểm H tiến gần đến gốc tọa độ? Khi H tiến xa sang phía bên phải thì sao?...

Thực hành 1 trang 72 Toán 11 Tập 1: Tìm các giới hạn sau:....

Hoạt động khám phá 2 trang 72 Toán 11 Tập 1: Cho hai hàm số y = f(x) = 2x và y = g(x) = $\frac{x}{x + 1}$ .....

Thực hành 2 trang 73 Toán 11 Tập 1: Tìm các giới hạn sau:.....

Hoạt động khám phá 3 trang 73 Toán 11 Tập 1: Giá cước vận chuyển bưu kiện giữa hai thành phố do một đơn vị được cho bởi bảng sau....:

Thực hành 3 trang 75 Toán 11 Tập 1: Cho hàm số ....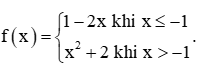

Hoạt động khám phá 4 trang 75 Toán 11 Tập 1: Cho hàm số $f (x) = \frac{1}{x}$ có đồ thị như Hình 3....

Thực hành 4 trang 76 Toán 11 Tập 1: Tìm các giới hạn sau:....

Vận dụng 1 trang 76 Toán 11 Tập 1: Một cái hồ đang chứa 200m³ nước mặn với nồng độ muối 10kg/m³. Người ta ngọt hóa nước hồ bằng cách bơm nước ngọt vào hồ với tốc độ 2m³/phút.....

Hoạt động khám phá 5 trang 77 Toán 11 Tập 1: Cho hàm số $f (x) = \frac{1}{x - 1}$ có đồ thị như Hình 4....

Thực hành 5 trang 78 Toán 11 Tập 1: Tìm các giới hạn sau....

Vận dụng 2 trang 78 Toán 11 Tập 1: Xét tình huống ở hoạt động khởi động đầu bài học. Gọi x là hoành độ điểm H. Tính diện tích S(x) của hình chữ nhật OHMK theo x. Diện tích này thay đổi như thế nào khi x → 0⁺ và khi x → +∞.....

Bài 1 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau:....

Bài 2 trang 79 Toán 11 Tập 1: Cho hàm số ....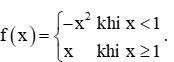

Bài 3 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau:....

Bài 4 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau:...

Bài 5 trang 79 Toán 11 Tập 1: Trong hồ có chứa 6 000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 30 gam/lít vào hồ với tốc độ 15 lít/phút.....

Bài 6 trang 79 Toán 11 Tập 1: Một thấu kính hội tụ có tiêu cự là f > 0 không đổi. Gọi d và d’ lần lượt là khoảng cách từ vật thật và ảnh của nó tới quang tâm O của thấu kính (Hình 5). Ta có công thức $\frac{1}{d} + \frac{1}{d'} = \frac{1}{f}$ hay $d' = \frac{d f}{d - f}$ ....

Xem thêm các bài giải SGK Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Giới hạn của dãy số

Bài 2: Giới hạn của hàm số

Bài 3: Hàm số liên tục

Bài tập cuối chương 3

Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian

Từ khóa :

Toán 11

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

164

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

137

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.