Với giải Luyện tập 2 trang 73 Toán lớp 8 Tập 1 Cánh diều chi tiết trong Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a khác 0) giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a khác 0)

Video bài giải Toán lớp 8 Bài 4: Đồ thị hàm số bậc nhất y = ax + b (a khác 0) - Cánh diều

Luyện tập 2 trang 73 Toán 8 Tập 1: Vẽ đồ thị của mỗi hàm số sau:

a) y = 3x;

b) y = 2x + 2.

Lời giải:

a) Đồ thị hàm số y = 3x.

Với x = 1 thì y = 3 . 1 = 3, ta được điểm A(1; 3) thuộc đồ thị của hàm số y = 3x.

Vậy đồ thị của hàm số y = 3x là đường thẳng đi qua hai điểm O(0; 0) và A(1; 3).

Khi đó, đồ thị hàm số y = 3x được biểu diễn như hình vẽ:

b) Đồ thị hàm số y = 2x + 2.

• Với x = 0 thì y = 2 . 0 + 2 = 0 + 2 = 2, ta được điểm M(0; 2) thuộc đồ thị của hàm số y = 2x + 2.

• Với y = 0 thì 2x + 2 = 0 suy ra x = – 1, ta được điểm N(– 1; 0) thuộc đồ thị của hàm số y = 2x + 2.

Vậy đồ thị của hàm số y = 2x + 2 là đường thẳng đi qua hai điểm M(0; 2) và N(– 1; 0).

Khi đó, đồ thị hàm số y = 2x + 2 được biểu diễn như hình vẽ:

 Lý thuyết Vẽ đồ thị của hàm số bậc nhất

Hàm số y = ax (a$\ne$0)

Để vẽ đồ thị của hàm số y = ax (a$\ne$0), ta có thể xác định điểm A(1; a) rồi vẽ đường thẳng đi qua hai điểm O và A.

Hàm số y = ax + b (a$\ne$0)

Để vẽ đồ thị của hàm số y = ax + b (a$\ne$0, b$\ne$0), ta có thể xác định hai điểm P(0; b) và Q$\left(-\frac{b}{a};0\right)$ rồi vẽ dường thẳng đi qua hai điểm đó.

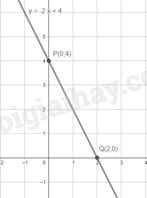
Ví dụ: Cho hàm số y = -2x + 4

Với x = 0 thì y =  4, ta được điểm P(0;4)