Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 8 Bài 2: Hình chóp tứ giác đều chi tiết sách Toán 8 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:

Giải bài tập Toán lớp 8 Bài 2: Hình chóp tứ giác đều

Video bài giải Toán lớp 8 Bài 2: Hình chóp tứ giác đều - Cánh diều

Giải Toán 8 trang 84 Tập 1

Khởi động trang 84 Toán 8 Tập 1: Trong thực tiễn ta thường gặp những vật thể có dạng như ở Hình 11.

Những hình khối có dạng như ở Hình 11 được gọi là hình gì?

Lời giải:

Những hình khối có dạng như ở Hình 11 được gọi là hình chóp tứ giác đều.

I. Hình chóp tứ giác đều

Hoạt động 1 trang 84 Toán 8 Tập 1: Thực hiện các hoạt động sau:

a) Vẽ trên giấy (hay bìa mỏng) 1 hình vuông và 4 hình tam giác với các cạnh và vị trí như ở Hình 12;

b) Cắt rời theo đường viền (màu đỏ) của hình vừa vẽ (phần tô màu) và gấp lại để được hình chóp tứ giác đều như ở Hình 13;

c) Quan sát hình chóp tứ giác đều ở Hình 13 và nêu số mặt, số cạnh của hình chóp tứ giác đều đó.

Lời giải:

a) Học sinh thực hiện theo hướng dẫn.

b) Học sinh thực hiện theo hướng dẫn.

c) Quan sát hình chóp tứ giác đều ở Hình 13, ta thấy hình chóp tứ giác đều có 5 mặt và 8 cạnh.

Hoạt động 2 trang 84 Toán 8 Tập 1: Quan sát hình chóp tứ giác đều ở Hình 14 và đọc tên các mặt, các cạnh, đỉnh của hình chóp tứ giác đều đó.

Lời giải:

Hình chóp tứ giác đều S.ABCD ở Hình 14 có:

• Các mặt là ABCD, SAB, SBC, SCD, SDA;

• Các cạnh là AB, BC, CD, DA, SA, SB, SC, SD;

• Đỉnh là S.

II. Diện tích xung quanh của hình chóp tứ giác đều

Giải Toán 8 trang 85 Tập 1

Luyện tập trang 85 Toán 8 Tập 1: Cho một hình chóp tứ giác đều có độ dài cạnh đáy bằng 10 cm và độ dài trung đoạn bằng 15 cm. Tính diện tích xung quanh của hình chóp tứ giác đều đó.

Lời giải:

Diện tích xung quanh của hình chóp tứ giác đều đó là:

$S_{xq}=\frac{1}{2}.\left(10.4\right).15=300\left(c{m}^2\right)$

III. Thể tích của hình chóp tứ giác đều

Bài tập

Giải Toán 8 trang 87 Tập 1

Bài 1 trang 87 Toán 8 Tập 1: Trong các miếng bìa ở hình 19a, 19b, 19c, 19d, 19e, miếng bìa nào có thể gấp lại (theo các nét đứt) để được hình chóp tứ giác đều?

Lời giải:

Hình chóp tứ giác đều có 5 mặt, trong đó có 1 mặt đáy là hình vuông và 4 mặt bên là các hình tam giác cân bằng nhau.

Quan sát hình 19 ta thấy trong các miếng bìa, chỉ có miếng bìa ở hình 19c thỏa mãn có 1 hình vuông và 4 hình tam giác cân bằng nhau nên khi gấp lại (theo các nét đứt) thì được hình chóp tứ giác đều.

Bài 2 trang 87 Toán 8 Tập 1: Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 7 cm và độ dài trung đoạn bằng 10 cm. Tính diện tích xung quanh của hình chóp tứ giác đều đó.

Lời giải:

Diện tích xung quanh của hình chóp tứ giác đều S.ABCD là:

$S_{xq}=\frac{1}{2}.\left(7.4\right).10=140\left(c{m}^2\right)$

Bài 3 trang 87 Toán 8 Tập 1: Cho một hình chóp tứ giác đều có độ dài cạnh đáy là 15 cm và chiều cao là 8 cm. Tính thể tích của hình chóp tứ giác đều đó.

Lời giải:

$V=\frac{1}{3}{.15}^2.8=600\left(c{m}^3\right)$

Bài 4 trang 87 Toán 8 Tập 1: Một mái che giếng trời có dạng hình chóp tứ giác đều với độ dài cạnh đáy khoảng 2,2 m và độ dài trung đoạn khoảng 2,8 m (Hình 20). Cần phải trả bao nhiêu tiền để làm mái che giếng trời đó? Biết rằng giá để làm mỗi mét vuông mái che được tính là 1 800 000 đồng (bao gồm tiền vật liệu và tiền công).

Lời giải:

Diện tích xung quanh của mái che giếng trời có dạng hình chóp tứ giác đều đó là:

$S_{xq}\approx \frac{1}{2}.\left(\mathrm{2,2}.4\right)\mathrm{.2,8}=\mathrm{12,32}\left(m^2\right)$.

Số tiền cần phải trả (bao gồm tiền vật liệu và tiền công) để làm mái che giếng trời đó là:

12,32 . 1 800 000 = 22 176 000 (đồng).

Video bài giảng Toán 8 Bài 2: Hình chóp tứ giác đều - Cánh diều

Xem thêm các bài giải SGK Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài 1: Hình chóp tam giác đều

Bài 2: Hình chóp tứ giác đều

Bài tập cuối chương 4

Chủ đề 2: Thực hành tạo dựng Hologram

Bài 1: Định lí Pythagore

Lý thuyết Hình chóp tứ giác đều

1. Khái niệm

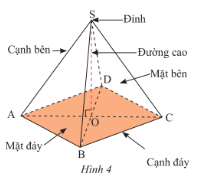
Hình chóp tứ giác đều có:

- Đáy là hình vuông.

- 4 cạnh bên bằng nhau.

- 4 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.

- 4 cạnh đáy bằng nhau là bốn cạnh của hình vuông đáy.

- Chân đường cao trùng với giao điểm của hai đường chéo của mặt đáy.

2. Công thức tính diện tích xung quanh của hình chóp tứ giác đều

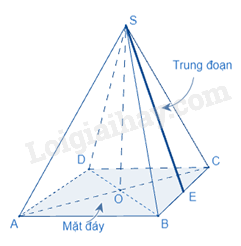
Diện tích xung quanh của hình chóp tam giác đều bằng nửa chu vi đáy với độ dài trung đoạn.

$S_{xq}=p.d$

($S_{xq}$ là diện tích xung quanh, p là nửa chu vi đáy, d là trung đoạn)

3. Công thức tính thể tích của hình chóp tứ giác đều

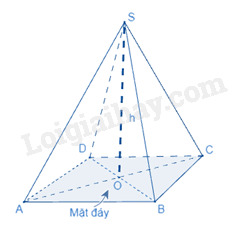
Thể tích của hình chóp tam giác đều (hình chóp tứ giác đều) bằng $\frac{1}{3}$ diện tích đáy nhân với chiều cao.

$V=\frac{1}{3}{S}_{đáy}.h$

(V là thể tích, $S_{đáy}$ là diện tích đáy, h là chiều cao)

Ví dụ: 

Cho hình chóp tứ giác đều sau:

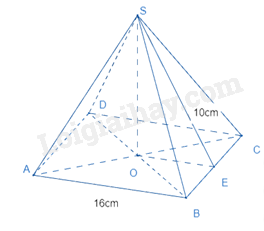
Thể tích của hình chóp là: $V=\frac{1}{3}.6.16.16=512(c{m}^3)$