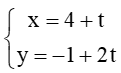Với giải Bài 32 trang 74 SBT Toán lớp 10 Cánh diều chi tiết trong Bài 3: Phương trình đường thẳng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài 3: Phương trình đường thẳng
Bài 32 trang 74 SBT Toán 10 Tập 2: Cho ba điểm A(- 2; 2), B(7; 5), C(4; - 5) và đường thẳng ∆: 2x + y – 4 = 0.
a) Tìm tọa độ điểm M thuộc ∆ và cách đều hai điểm A và B.
b*) Tìm tọa độ điểm N thuộc ∆ sao cho || có giá trị nhỏ nhất.
Lời giải:
a) Do M thuộc đường thẳng ∆ nên M(t; 4 – 2t).
Suy ra =(t+2;2-2t) và =(t-7;-1-2t).
Do M cách đều 2 điểm A, B nên MA = MB.
Hay ||= ||
⇔ 5t2 – 4t + 8 = 5t2 – 10t + 50
⇔ 6t = 42
⇔ t = 7
Vậy M(7; -10).
b) Do N thuộc đường thẳng ∆ nên N(m; 4 – 2m).
Suy ra =(-2-2;2m-2), =(7-m;2m+1) và =(4-1;2m-9)
= (9-3m;6m-10)
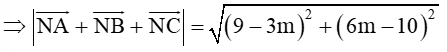
Gọi A= (9-3m)2+(6m-10)2
A=45m2 - 174m+181=45
Suy ra GTNN của || là đạt được khi m=
Hay .
Xem thêm lời giải SBT Toán lớp 10 Cánh diều hay, chi tiết khác:
Bài 24 trang 73 SBT Toán 10 Tập 2: Cho đường thẳng ∆: 2x – 3y + 5 = 0. Vectơ nào dưới đây là một vectơ pháp tuyến của ∆?...
Bài 26 trang 73 SBT Toán 10 Tập 2: Cho đường thẳng ∆: 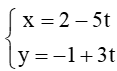 . Trong các điểm có tọa độ dưới đây, điểm nào nằm trên đường thẳng ∆?...
. Trong các điểm có tọa độ dưới đây, điểm nào nằm trên đường thẳng ∆?...
Bài 27 trang 73 SBT Toán 10 Tập 2: Cho đường thẳng ∆: x – 3y + 4 = 0. Phương trình nào dưới đây là phương trình tham số của ∆?...
Bài 28 trang 73 SBT Toán 10 Tập 2: Cho đường thẳng ∆:  . Phương trình nào dưới đây là phương trình tổng quát của ∆?...
. Phương trình nào dưới đây là phương trình tổng quát của ∆?...
Bài 29 trang 73 SBT Toán 10 Tập 2: Cho tam giác ABC, biết tọa độ trung điểm các cạnh BC, CA, AB lần lượt là M(-1; 1), N(3; 4), P(5; 6)...
Bài 30 trang 73 SBT Toán 10 Tập 2: Cho tam giác ABC có A(3; 7), B(-2; 2), C(6; 1). Viết phương trình tổng quát của các đường cao của tam giác ABC...
Bài 31 trang 74 SBT Toán 10 Tập 2: Cho đường thẳng ∆: 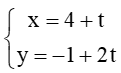 và điểm A(2; 1). Hai điểm M, N nằm trên ∆...
và điểm A(2; 1). Hai điểm M, N nằm trên ∆...
Bài 32 trang 74 SBT Toán 10 Tập 2: Cho ba điểm A(- 2; 2), B(7; 5), C(4; - 5) và đường thẳng ∆: 2x + y – 4 = 0...
Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:
SBT Toán 10 Bài 2: Biểu thức tọa độ của các phép toán vectơ
SBT Toán 10 Bài 3: Phương trình đường thẳng
SBT Toán 10 Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng
SBT Toán 10 Bài 5: Phương trình đường tròn
SBT Toán 10 Bài 6: Ba đường conic