Với giải Bài 104 trang 99 SBT Toán lớp 7 Cánh diều chi tiết trong Bài tập cuối chương VII giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài tập cuối chương VII

Bài 104 trang 99 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có AB < AC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.

a) Chứng minh AC = EB và AC song song với EB.

b) Gọi I là một điểm trên AC, K là một điểm trên EB sao cho AI = EK. CHứng minh ba điểm I, M, K thẳng hàng.

c) Từ E kẻ EH vuông góc với BC tại H. Cho biết $\widehat{HBE}=50°;\widehat{MEB}=25°$. Tính số đo các góc HEB và HEM.

Lời giải:

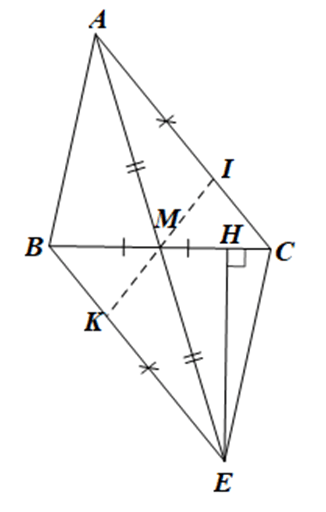
a) Xét ∆AMC và ∆EMB có:

AM = ME (giả thiết),

$\widehat{AMC}=\widehat{EMB}$ (hai góc đối đỉnh),

BM = CM (vì M là trung điểm của BC)

Do đó ∆AMC = ∆EMB (c.g.c)

Suy ra AC = EB (hai cạnh tương ứng) và $\widehat{MAC}=\widehat{MEB}$ (hai góc tương ứng)

Mà $\widehat{MAC}$ và $\widehat{MEB}$ ở vị trí so le trong nên AC // BE.

Vậy AC = EB và AC song song với EB.

b) Xét ∆AMI và ∆EMK có:

AM = ME (giả thiết),

$\widehat{MAI}=\widehat{MEK}$ (do $\widehat{MAC}=\widehat{MEB}$),

AI = EK (giả thiết)

Do đó ∆AMI = ∆EMK (c.g.c)

Suy ra $\widehat{AMI}=\widehat{EMK}$ (hai góc tương ứng)

Mà $\widehat{AMI}+\widehat{IME}=180°$ (hai góc kề bù)

Suy ra $\widehat{EMK}+\widehat{IME}=180°$

Hay $\widehat{IMK}=180°$

Do đó ba điểm I, M, K thẳng hàng.

Vậy ba điểm I, M, K thẳng hàng.

c) Trong tam giác HBE vuông tại H có:

$\widehat{HBE}+\widehat{HEB}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Suy ra $\widehat{HEB}=90°-\widehat{HBE}=90°-50°=40°$ .

Ta có $\widehat{HEB}=\widehat{HEM}+\widehat{MEB}$ (hai góc kề nhau)

Hay $40°=\widehat{HEM}+25°$

Suy ra $\widehat{HEM}=40°-25°=15°$ .

Vậy $\widehat{HEB}=40°;\widehat{HEM}=15°$.