Với giải sách bài tập Toán 7 Bài 3: Hai tam giác bằng nhau sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 3: Hai tam giác bằng nhau

Giải SBT Toán 7 trang 72 Tập 2

Bài 19 trang 72 sách bài tập Toán lớp 7 Tập 2: Quan sát các hình 9a, 9b, viết các cặp tam giác bằng nhau.

Lời giải:

Hình a)

Xét tam giác XYT và tam giác XOT có:

+) XY = XO, YT = OT, XT là cạnh chung;

+) $\widehat{T\text{XY}}=\widehat{T\text{X}O},\hat{Y}=\hat{O},\widehat{XTY}=\widehat{OT\text{X}}$ .

Do đó ∆XYT = ∆XOT.

Vậy ∆XYT = ∆XOT.

Hình b)

Xét tam giác ABC và tam giác NPM có:

+) AB = NP, BC = PM, AC = NM;

+) $\hat{A}=\hat{N},\hat{B}=\hat{P},\hat{C}=\hat{M}$ .

Do đó ∆ABC = ∆NPM.

Vậy ∆ABC = ∆NPM.

Bài 20 trang 72 sách bài tập Toán lớp 7 Tập 2: Cho hai tam giác bằng nhau: tam giác ABC và một tam giác có ba đỉnh là X, Y, Z. Viết kí hiệu sự bằng nhau của hai tam giác đó trong mỗi trường hợp sau:

a) $\hat{A}=\hat{X},\hat{B}=\hat{Z}$ ;

b) AB = XY, BC = YZ.

Lời giải:

Vì tam giác ABC và tam giác có ba đỉnh X, Y, Z bằng nhau nên để viết được kí hiệu sự bằng nhau của hai tam giác đó, ta sẽ tìm các đỉnh tương ứng của hai tam giác này.

a) Do $\hat{A}=\hat{X},\hat{B}=\hat{Z}$ nên đỉnh A tương ứng với đỉnh X, đỉnh B tương ứng với đỉnh Z.

Khi đó đỉnh C tương ứng với đỉnh Y.

Do đó kí hiệu sự bằng nhau của hai tam giác này là ∆ABC = ∆XZY.

Vậy ∆ABC = ∆XZY.

b) Ta cóAB = XY, BC = YZnên đỉnh B tương ứng với đỉnh Y.

Khi đó đỉnh A tương ứng với đỉnh X và đỉnh C tương tứng với đỉnh Z.

Do đó kí hiệu sự bằng nhau của hai tam giác này là∆ABC = ∆XYZ.

Vậy ∆ABC = ∆XYZ.

Bài 21 trang 72 sách bài tập Toán lớp 7 Tập 2: Bạn Sơn cho rằng “Nếu độ dài các cạnh của tam giác ABC đều là số tự nhiên và ∆ABC = ∆MNP thì tổng chu vi của tam giác ABC và tam giác MNP là số lẻ”. Bạn Sơn nói như vậy có đúng không? Vì sao?

Lời giải:

Vì ∆ABC = ∆MNP nên AB = MN, BC = NP, AC = MP (các cặp cạnh tương ứng).

Suy ra AB + BC + AC = MN + NP + MP.

Hay chu vi của tam giác MNP bằng chu vi của tam giác ABC.

Do độ dài các cạnh của tam giác ABC đều là số tự nhiên nên chu vi của tam giác ABC cũng là số tự nhiên.

Gọi chu vi của tam giác ABC là x (x là số tự nhiên).

Khi đó, chu vi của tam giác MNP là x.

Do đó, tổng chu vi của tam giác ABC và tam giác MNP là:

x + x = 2x (là số chẵn).

Vậy bạn Sơn nói không đúng.

Giải SBT Toán 7 trang 73 Tập 2

Bài 22 trang 73 sách bài tập Toán lớp 7 Tập 2: Cho ∆ABC = ∆DEG có AB = 4 dm, BC = 7 dm, CA = 9,5 dm. Tính chu vi của tma giác DEG.

Lời giải:

Vì ∆ ABC = ∆ DEG nên ta có: AB = DE, BC = EG, AC = DG (các cặp cạnh tương ứng).

Do đó chu vi của tam giác DEG bằng chu vi của tam giác ABC.

Mà chu vi tam giác ABC là: 4 + 7 + 9,5 = 20,5 (dm).

Do đó chu vi tam giác DEG bằng 20,5 dm.

Vậy chu vi tam giác DEG bằng 20,5 dm.

Bài 23 trang 73 sách bài tập Toán lớp 7 Tập 2: Cho ∆ABC = ∆GIK có số đo $\hat{G},\hat{I},\hat{K}$ tỉ lệ với 2; 3; 4. Tính số đo mỗi góc của tam giác ABC.

Lời giải:

Vì số đo $\hat{G},\hat{I},\hat{K}$ tỉ lệ với 2; 3; 4 nên ta có: $\frac{\hat{G}}{2}=\frac{\hat{I}}{3}=\frac{\hat{K}}{4}$ .

Xét DGIK có $\hat{G}+\hat{I}+\hat{K}={180}^o$ (tổng ba góc của một tam giác).

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

$\frac{\hat{G}}{2}=\frac{\hat{I}}{3}=\frac{\hat{K}}{4}=\frac{\hat{G}+\hat{I}+\hat{K}}{9}=\frac{180°}{9}=20°$

Suy ra

• $\hat{G}=2.20°=40°;$

• $\hat{I}=3.20°=60°;$

• $\hat{K}=4.20°=80°.$

Do ∆ABC = ∆GIK nên $\hat{A}=\hat{G},\hat{B}=\hat{I},\hat{C}=\hat{K}$ (các cặp góc tương ứng).

Mà $\hat{G}=40°,\hat{I}=60°,\hat{K}=80°$

Suy ra $\hat{A}=40°,\hat{B}=60°,\hat{C}=80°.$

Vậy $\hat{A}=40°,\hat{B}=60°,\hat{C}=80°.$

Bài 24 trang 73 sách bài tập Toán lớp 7 Tập 2: Cho ∆ABC = ∆XYZ có 3BC = 5AB, YZ – XY = 10 cm và AC = 35 cm. Tính độ dài mỗi cạnh của tam giác XYZ.

Lời giải:

Do ∆ABC = ∆XYZ (giả thiết)

Nên AB = XY, BC = YZ, AC = XZ (các cặp cạnh tương ứng)

Mà AC = 35 cm nên XZ = 35 cm.

Ta có YZ – XY = 10 (cm) suy ra BC – AB = 10 (cm).

Hay BC = AB +10.

Mà 3BC = 5AB

Suy ra 3(AB + 10) = 5AB

Hay 5AB – 3AB = 30

Do đó 2AB = 30

Suy ra AB = 15 (cm)

Khi đó BC = 25 (cm)

Lại có AB = XY, BC = YZ nên XY = 15 (cm) và YZ = 25 (cm).

Vậy XY = 15 cm, YZ = 25 cm, XZ = 35 cm.

Bài 25 trang 73 sách bài tập Toán lớp 7 Tập 2: Cho ∆ABC = ∆XYZ, có $\hat{A}+\hat{Y}=120°$ và $\hat{A}-\hat{Y}=40°$ . Tính số đo mỗi góc của từng tam giác trên.

Lời giải:

Do $\hat{A}+\hat{Y}=120°$ và $\hat{A}-\hat{Y}=40°$ nên $2\hat{A}=120°+40°=160°$

Suy ra $\hat{A}=160°:2=80°$

Do đó $\hat{Y}=120°-\hat{A}=120°-80°=40°$

Vì ∆ABC = ∆XYZ (giả thiết)

Nên $\hat{A}=\hat{X},\hat{B}=\hat{Y},\hat{C}=\hat{Z}$ (các cặp góc tương ứng).

Mà $\hat{A}=80°,\hat{Y}=40°$

Suy ra $\hat{X}=80°,\hat{B}=40°$

Xét ∆ABC có: $\hat{C}+\hat{B}+\hat{A}=180°$ (tổng ba góc của một tam giác).

Do đó $\hat{C}=180°-\hat{B}-\hat{A}=180°-40°-80°=60°$

Suy ra $\hat{Z}=60°$ .

Vậy $\hat{A}=80°,\hat{B}=40°,\hat{C}=60°,\hat{X}=80°,\hat{Y}=40°,\hat{Z}=60°.$

Bài 26 trang 73 sách bài tập Toán lớp 7 Tập 2: Cho ∆ABC = ∆MNP. Hai tia phân giác của góc B và C cắt nhau tại O tạo thành góc BOC bằng 120°. Tính tổng số đo các góc MNP và MPN của tam giác MNP.

Lời giải:

Vì BO là phân giác của góc ABC nên $\widehat{ABO}=\widehat{CBO}=\frac{\widehat{ABC}}{2}$

Vì CO là phân giác của góc ACB nên $\widehat{ACO}=\widehat{BCO}=\frac{\widehat{ACB}}{2}$

Xét DCOB ta có: $\widehat{BOC}+\widehat{OBC}+\widehat{OCB}=180°$ (tổng ba góc của một tam giác).

Suy ra $\widehat{OBC}+\widehat{OCB}=180°-\widehat{BOC}=180°-120°=60°.$

Mà $\widehat{CBO}=\frac{\widehat{ABC}}{2},\widehat{BCO}=\frac{\widehat{ACB}}{2}.$

Suy ra $\frac{\widehat{ABC}}{2}+\frac{\widehat{ACB}}{2}=60°$

Do đó $\widehat{ABC}+\widehat{ACB}=2.60°=120°.$

Mặt khác ∆ABC = ∆MNP nên ta có:

$\widehat{ABC}=\widehat{MNP}$ và $\widehat{ACB}=\widehat{MPN}$ (các cặp góc tương ứng).

Suy ra $\widehat{MNP}+\widehat{MPN}=\widehat{ABC}+\widehat{ACB}=120°$

Vậy $\widehat{MNP}+\widehat{MPN}=120°$.

Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:

SBT Toán 7 Bài 2 : Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

SBT Toán 7 Bài 3 : Hai tam giác bằng nhau

SBT Toán 7 Bài 4 : Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh

SBT Toán 7 Bài 5 : Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh

SBT Toán 7 Bài 6 : Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc

Lý thuyết Hai tam giác bằng nhau

– Định nghĩa: Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.

Ví dụ: Cho hai tam giác ABC và A’B’C’ như hình vẽ dưới đây:

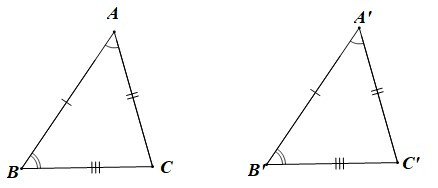
Hai tam giác này có bằng nhau không? Vì sao?

Hướng dẫn giải

Xét tam giác ABC và tam giác A'B'C' có:

+) AB = A'B', AC = A'C', BC = B'C';

+) $\widehat{\mathrm{A}}=\widehat{{\mathrm{A}}^{\text{'}}},\widehat{\mathrm{B}}=\widehat{{\mathrm{B}}^{\text{'}}},\widehat{\mathrm{C}}=\widehat{{\mathrm{C}}^{\text{'}}}.$ 

Do đó hai tam giác ABC và A’B’C’ là hai tam giác bằng nhau.

– Khi tam giác ABC và tam giác A'B'C' bằng nhau thì ta kí hiệu là: DABC = DA'B'C'.

– Quy ước: Khi viết hai tam giác bằng nhau, tên đỉnh của hai tam giác đó phải viết theo đúng thứ tự tương ứng với sự bằng nhau.

- Chú ý:

+ Nếu AB = A'B', AC = A'C', BC = B'C' và $\widehat{\mathrm{A}}=\widehat{{\mathrm{A}}^{\text{'}}},\widehat{\mathrm{B}}=\widehat{{\mathrm{B}}^{\text{'}}},\widehat{\mathrm{C}}=\widehat{{\mathrm{C}}^{\text{'}}}$thì DABC = DA'B'C'.

+ Nếu DABC = DA'B'C' thì AB = A'B', AC = A'C', BC = B'C' và $\widehat{\mathrm{A}}=\widehat{{\mathrm{A}}^{\text{'}}},$$\widehat{\mathrm{B}}=\widehat{{\mathrm{B}}^{\text{'}}},$ $\widehat{\mathrm{C}}=\widehat{{\mathrm{C}}^{\text{'}}}.$

Ở đây:

• Hai góc A và A' (B và B', C và C') là hai góc tương ứng;

• Hai cạnh AB và A'B' (BC và B'C', AC và A'C') là hai cạnh tương ứng.

Ví dụ: Cho hai tam giác ABC và DEF như hình vẽ dưới đây:

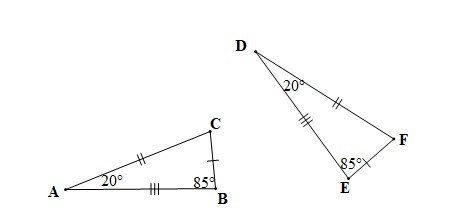
Hai tam giác ABC và DEF có bằng nhau không? Nếu bằng nhau hãy viết kí hiệu bằng nhau của hai tam giác đó.

Hướng dẫn giải

Xét tam giác FDE có $\widehat{\mathrm{F}}+\widehat{\mathrm{D}}+\widehat{\mathrm{E}}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{\mathrm{F}}=180°-\widehat{\mathrm{E}}-\widehat{\mathrm{D}}$

Hay $\widehat{\mathrm{F}}=180°-85°-20°=75°$ 

Xét tam giác BCA ta cũng có: $\widehat{\mathrm{B}}+\widehat{\mathrm{C}}+\widehat{\mathrm{A}}=180°$(định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{\mathrm{C}}=180°-\widehat{\mathrm{B}}-\widehat{\mathrm{A}}$

Hay $\widehat{\mathrm{C}}=180°-85°-30°=75°$

Xét tam giác FDE và tam giác BCA có:

+) AB = DE, AC = DF, BC = EF

+) $\widehat{\mathrm{A}}=\widehat{\mathrm{D}}\left(=20°\right),\widehat{\mathrm{B}}=\widehat{\mathrm{E}}\left(=85°\right),\widehat{\mathrm{C}}=\widehat{\mathrm{F}}\left(=75°\right)$ 

Do đó DABC = DDEF.