Với giải Vở bài tập Toán 7 Bài 3: Hai tam giác bằng nhau sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 7. Mời các bạn đón xem:

Giải VBT Toán lớp 7 Bài 3: Hai tam giác bằng nhau

I. Kiến thức trọng tâm

Câu 1 trang 77 vở bài tập Toán lớp 7 Tập 2:

- Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng………. và các góc tương ứng………….

- Khi hai tam giác ABC và A’B’C’ bằng nhau thì ta kí hiệu là: ………………………

(Hình 20)

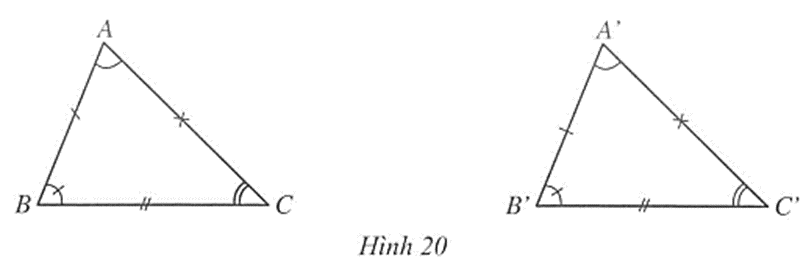
Quy ước: Khi viết hai tam giác bằng nhau, tên đỉnh của hai tam giác đó phải viết theo đúng thứ tự tương ứng với sự bằng nhau.

+ Nếu AB = A’B’, BC = B’C’, CA = C’A’ và $\hat{A}=\widehat{A\text{'}}$, $\hat{B}=\widehat{B\text{'}}$, $\hat{C}=\widehat{C\text{'}}$ thì ∆ABC = …

+ Nếu ∆ABC = ∆A’B’C’ thì AB = …., …. = B’C’, CA = …. và ….= $\widehat{A\text{'}}$, $\hat{B}$=…., …= $\hat{C}\text{'}$

Lời giải:

- Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.

- Khi hai tam giác ABC và A’B’C’ bằng nhau thì ta kí hiệu là: ∆ABC = ∆A’B’C’.

+ Nếu AB = A’B’, BC = B’C’, CA = C’A’ và $\hat{A}=\widehat{A\text{'}}$, $\hat{B}=\widehat{B\text{'}}$, $\hat{C}=\widehat{C\text{'}}$ thì ∆ABC = ∆A’B’C’.

+ Nếu ∆ABC = ∆A’B’C’ thì AB = A’B’, BC = B’C’, CA = C’A’ và $\hat{A}=\widehat{A\text{'}}$, $\hat{B}=\widehat{B\text{'}}$, $\hat{C}=\widehat{C\text{'}}$.

II. Luyện tập

• Câu 1 trang 77 vở bài tập Toán lớp 7 Tập 2:Cho ∆ABC = ∆MNP, AC = 4 cm, $\widehat{\mathrm{MPN}}$ = 45^o. Tính độ dài cạnh MP và số đo góc ACB.

  Lời giải:

  Vì ∆ABC = ∆MNP nên

  AC = MP (hai cạnh tương ứng); $\widehat{\mathrm{ACB}}$ = $\widehat{\mathrm{MPN}}$(hai góc tương ứng)

  Mà AC = 4 cm và $\widehat{\mathrm{MPN}}$ = 45^o nên MP = 4 cm, $\widehat{\mathrm{ACB}}$= 45^o.

• III. Bài tập

  • Câu 1 trang 77 vở bài tập Toán lớp 7 Tập 2:Cho biết ∆ABC = ∆DEG, AB = 3cm, BC = 4 cm, CA = 6 cm. Tính độ dài các cạnh của tam giác DEG

    Lời giải:

    Vì ∆ABC = ∆DEG nên AB = DE, BC = EG, CA = GD

    Mà AB = 3cm, BC = 4 cm, CA = 6 cm nên DE = 3 cm, EG = 4 cm, GD = 6 cm.

  • Câu 2 trang 77 vở bài tập Toán lớp 7 Tập 2:Cho ∆PQR = ∆IHK, $\hat{P}$ = 71^o, $\hat{Q}$ = 49^o. Tính số đo góc K của tam giác IHK.

    Lời giải:

    Ta có: $\hat{P}$+ $\hat{Q}$+ $\hat{R}$= 180^o (tổng ba góc của một tam giác), $\hat{P}$ = 71^o, $\hat{Q}$ = 49^o.

    Suy ra: $\hat{R}$= 180^o – ( $\hat{P}$+ $\hat{Q}$ ) = 180^o – (71^o + 49^o) = 60^o

    Do ∆PQR = ∆IHK nên $\hat{R}$= $\hat{K}$(hai góc tương ứng). Suy ra $\hat{K}$= 60^o.

  • Câu 3 trang 78 vở bài tập Toán lớp 7 Tập 2:Cho ∆ABC = ∆MNP và $\hat{A}$+ $\hat{N}$= 125^o. Tính số đo góc P.

    Lời giải:

    Vì ∆ABC = ∆MNP nên $\hat{A}$= $\hat{M}$( hai góc tương ứng)

    Do $\hat{A}$+ $\hat{N}$= $\hat{M}$+ $\hat{N}$Mà $\hat{A}$+ $\hat{N}$= 125^o nên $\hat{M}$+ $\hat{N}$= 125^o.

    Ta có $\hat{M}$+ $\hat{N}$+ $\hat{P}$= 180^o (tổng ba góc của một tam giác)

    Suy ra 125^o + $\hat{P}$= 180^o vì thế $\hat{P}$= 180^o – 125^o = 55^o.

  • Câu 4 trang 78 vở bài tập Toán lớp 7 Tập 2:Cho tam giác ABC và điểm M thuộc cạnh BC thoả mãn ∆AMB = ∆AMC (Hình 21). Chứng minh rằng:

    a) M là trung điểm của đoạn thẳng BC;

    b) Tia AM là tia phân giác của góc BAC và AM $\perp$ BC.

    Lời giải:

    Vì ∆AMB = ∆AMC nên: MB = MC (hai cạnh tương ứng);

    $\widehat{\mathrm{BAM}}$= $\widehat{\mathrm{CAM}}$, $\widehat{\mathrm{AMB}}$= $\widehat{\mathrm{AMC}}$(hai góc tương ứng)

    a) Do điểm M nằm giữa hai điểm B, C và MB = MC nên M là trung điểm của đoạn thẳng BC.

    b) Do tia AM nằm trong góc BAC và $\widehat{\mathrm{BAM}}$= $\widehat{\mathrm{CAM}}$nên tia AM là tia phân giác của góc BAC

    Ta có $\widehat{\mathrm{AMB}}$+ $\widehat{\mathrm{AMC}}$= 180^o (hai góc kề bù) và $\widehat{\mathrm{AMB}}$= $\widehat{\mathrm{AMC}}$nên $\widehat{\mathrm{AMB}}$= $\widehat{\mathrm{AMC}}$= 90^o.

    Vậy AM $\perp$ BC.

  • Câu 5 trang 78 vở bài tập Toán lớp 7 Tập 2: Cho Hình 22, ở đó ∆OAB = ∆OCD. Chứng minh a // b.

    

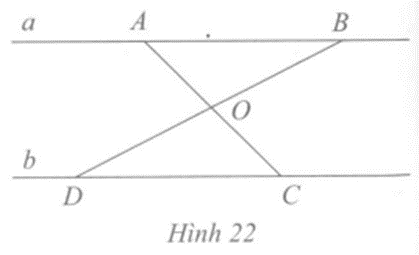
    Lời giải:

    Ta có ∆OAB = ∆OCD nên $\widehat{\mathrm{OAB}}$= $\widehat{\mathrm{OCD}}$

    Lại có $\widehat{\mathrm{OAB}}$và $\widehat{\mathrm{OCD}}$là hai góc so le trong

    Suy ra a // b.