Với giải Vở bài tập Toán 7 Bài 1: Tổng các góc của một tam giác sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 7. Mời các bạn đón xem:

Giải VBT Toán lớp 7 Bài 1: Tổng các góc của một tam giác

I. Kiến thức trọng tâm

Câu 1 trang 67 vở bài tập Toán lớp 7 Tập 2:

- Tổng ba góc trong một tam giác bằng………………..

- Tam giác có 3 góc ………. gọi là tam giác nhọn.

Tam giác có một góc……….. gọi là tam giác vuông.

Tam giác có một góc…………..gọi là tam giác tù.

- Tổng hai góc nhọn trong một tam giác vuông bằng……………

Lời giải:

- Tổng ba góc trong một tam giác bằng 180^o.

- Tam giác có 3 góc nhọn gọi là tam giác nhọn.

Tam giác có một góc vuông gọi là tam giác vuông.

Tam giác có một góc tù gọi là tam giác tù.

- Tổng hai góc nhọn trong một tam giác vuông bằng 90^o.

II. Luyện tập

• Câu 1 trang 67 vở bài tập Toán lớp 7 Tập 2:Cho tam giác đều ABC. Tính số đo mỗi góc của tam giác đó

  Lời giải:

  Tam giác ABC đều nên ba góc ở các đỉnh A, B, C bằng nhau. Giả sử $\hat{A}$ = $\hat{B}$ = $\hat{C}$ = x. Ta có $\hat{A}$ + $\hat{B}$ + $\hat{C}$ = 180^o (tổng ba góc của một tam giác).

  Hay x + x + x = 180^o. Suy ra 3.x = 180^o. Do đó x = 60^o.

  Vậy $\hat{A}=\hat{B}=\hat{C}=60°$.

• Câu 2 trang 67 vở bài tập Toán lớp 7 Tập 2:Toà tháp Capital Gate (thuộc Các Tiểu vương quốc Ả - Rập Thống nhất) nghiêng 18^o so với phương thẳng đứng (góc nghiêng biểu diễn như Hình 1). Tính độ nghiêng của tháp so với phương nằm ngang.

  Lời giải:

  

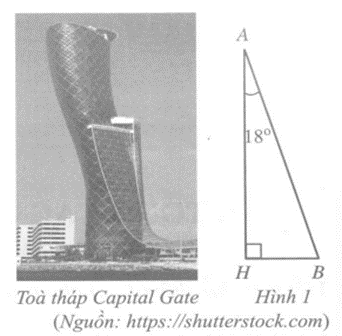
  Vì tam giác AHB vuông tại H nên $\hat{A}+\hat{B}$ = 90^o

  (tổng hai góc nhọn trong tam giác vuông)

  Suy ra: 18^o + $\hat{B}$ = 90^o

  $\hat{B}$ = 90^o – 18^o

  $\hat{B}$ = 72^o

  Vậy độ nghiêng của tháp so với phương nằm ngang là 72^o.

• III. Bài tập

• Câu 1 trang 68 vở bài tập Toán lớp 7 Tập 2:Một khung thép có dạng hình tam giác ABC với số đo các góc ở đỉnh B và đỉnh C cùng bằng 23^o (Hình 2). Tính số đo góc ở đỉnh A

  

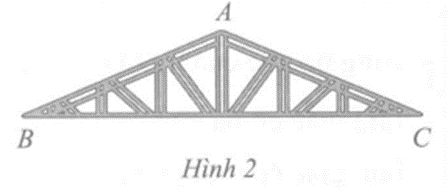
  Lời giải:

  Ta có $\hat{A}$ + $\hat{B}$ + $\hat{C}$ = 180^o (tổng ba góc của một tam giác)

  $\hat{A}$ = 180^o – ( $\hat{B}$ + $\hat{C}$ ) = 180^o – (23^o + 23^o) = 134^o

  Vậy $\hat{A}$ = 134^o

• Câu 2 trang 68 vở bài tập Toán lớp 7 Tập 2:Hình 3 biểu diễn một chiếc cầu trượt gồm máng trượt và thang leo. Tính độ nghiêng của máng trượt so với phương thẳng đứng biết rằng độ nghiêng của máng trượt so với mặt đất là 38^o.

  

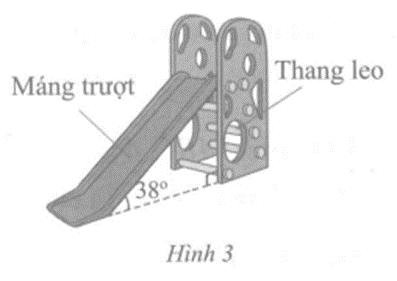
  Lời giải:

  Gọi x là số đo chỉ độ nghiêng của máng trượt so với phương thẳng đứng.

  Ta có: 38^o + x = 90^o (tổng hai góc nhọn trong một tam giác vuông)

  Suy ra: x = 90^o – 38^o Hay x = 52^o.

  Vậy độ nghiêng của máng trượt so với phương thẳng đứng là 52^o

• Câu 3 trang 68 vở bài tập Toán lớp 7 Tập 2:Trong Hình 4 MN // BC. Tính số đo góc C

  

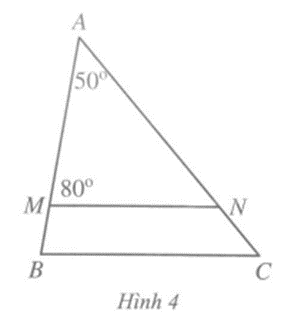
  Lời giải:

  Xét tam giác ANM, ta có

  $\hat{A}+\widehat{\mathrm{AMN}}+\widehat{\mathrm{ANM}}=$180° (tổng ba góc trong một tam giác)

  50^o + 80^o + $\widehat{\mathrm{ANM}}$ = 180^o

  $\widehat{\mathrm{ANM}}$ = 180^o – (50^o + 80^o) = 50^o

  Vì MN // BC nên $\widehat{\mathrm{ANM}}$ = $\widehat{\mathrm{ACB}}$ = 50^o (hai góc đồng vị)

  Vậy $\hat{C}$ = 50^o

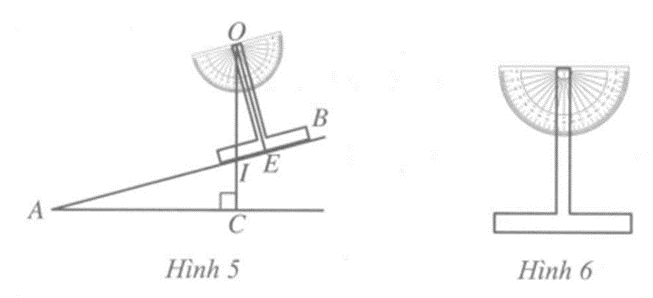
• Câu 4 trang 69 vở bài tập Toán lớp 7 Tập 2:Hình 5 biểu diễn mặt cắt đứng của một đường lên dốc AB. Để đo độ dốc của con đường biểu diễn bởi góc nhọn BAC tạo bởi đường thẳng AB với phương nằm ngang AC, người ta làm như sau:

  - Làm một thước chữ T như hình 6;

  - Đặt thước chữ T dọc theo cạnh AB như hình 5, $\mathrm{OE}\perp \mathrm{AB}$;

  - Buộc một sợi dây vào chân O của thước chữ T và buộc một vật nặng vào đầu dây còn lại, sau đó thả vật nặng để sợi dây có phương thẳng đứng (trong xây dựng gọi là thả dây dọi);

  - Tính góc BAC, biết rằng dây dọi OI tạo với trục OE của thước chữ T một góc 15^o.

  

  Lời giải:

  Vì tam giác AIC vuông tại C nên

  $\widehat{\mathrm{BAC}}$ + $\widehat{\mathrm{AIC}}$ = 90^o (tổng hai góc nhọn trong tam giác vuông).

  Tương tự, tam giác OIE vuông tại E nên $\widehat{\mathrm{COE}}$ + $\widehat{\mathrm{OIE}}$ = 90^o.

  Suy ra $\widehat{\mathrm{BAC}}$ + $\widehat{\mathrm{AIC}}$ = $\widehat{\mathrm{COE}}$ + $\widehat{\mathrm{OIE}}$. Mà $\widehat{\mathrm{AIC}}$ = $\widehat{\mathrm{OIE}}$ (hai góc đối đỉnh)

  Do đó $\widehat{\mathrm{BAC}}$ = $\widehat{\mathrm{COE}}$ = 15°

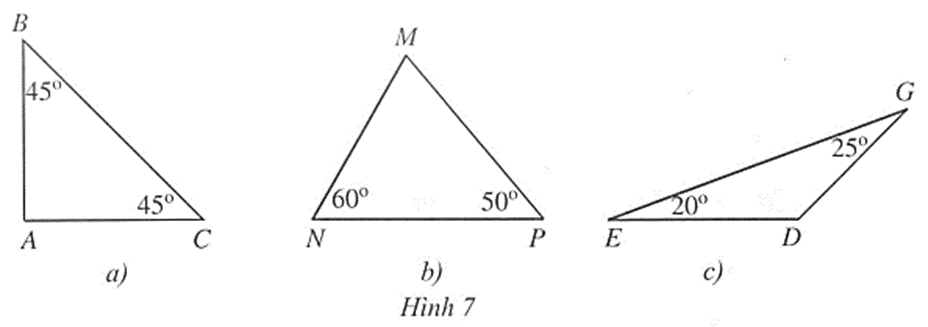
• Câu 5 trang 70 vở bài tập Toán lớp 7 Tập 2:Trong Hình 7, tam giác nào là tam giác nhọn? Tam giác vuông? Tam giác tù? Vì sao?

  

  Lời giải:

  Ở Hình 7a, ta có $\hat{A}$ + 45^o + 45^o = 180^o (tổng ba góc của một tam giác)

  Suy ra $\hat{A}$ = 180^o – (45^o +45^o) = 90^o

  Vì $\hat{A}$ = 90^o nên tam giác ABC là tam giác vuông

  Ở Hình 7b, ta có: $\hat{M}$ + 60^o + 50^o = 180^o (tổng ba góc của một tam giác)

  Suy ra $\hat{M}$ = 180^o – (60^o +50^o) = 70^o

  Vì Suy ra $\hat{M}$ < 90^o, $\hat{N}$ < 90^o, $\hat{P}$ < 90^o nên tam giác MNP là tam giác nhọn

  Ở Hình 7c, ta có: $\hat{D}$ + 20^o + 25^o = 180^o (tổng ba góc của một tam giác)

  Suy ra $\hat{D}$ = 180^o – (20^o + 25^o) = 135^o

  Vì Suy ra $\hat{D}$> 90^o nên tam giác DEG là tam giác tù.

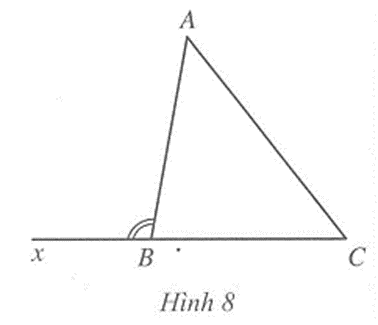
• Câu 6 trang 70 vở bài tập Toán lớp 7 Tập 2:Quan sát Hình 8. Chứng minh $\widehat{\mathrm{xBA}}$= $\hat{A}$+ $\hat{C}$

  

  Lời giải:

  Xét tam giác ABC, ta có:

  $\widehat{\mathrm{ABC}}$ + $\hat{A}$ + $\hat{C}$ = 180^o (tổng ba góc của một tam giác)

  Suy ra $\hat{A}$ + $\hat{C}$ = 180^o – $\widehat{\mathrm{ABC}}$ (1)

  Mặt khác $\widehat{\mathrm{xBA}}$ + $\widehat{\mathrm{ABC}}$ = 180^o (hai góc kề bù)

  Suy ra $\widehat{\mathrm{xBA}}$ = 180^o – $\widehat{\mathrm{ABC}}$ (2)

  Từ (1) và (2) suy ra $\widehat{\mathrm{xBA}}$ = $\hat{A}$ + $\hat{C}$ .

•