Với giải Bài 7 trang 77 Toán lớp 10 Cánh diều chi tiết trong Bài 2: Giải tam giác. Tính diện tích tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 2: Giải tam giác. Tính diện tích tam giác
Bài 7 trang 77 Toán lớp 10: Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là và . Biết khoảng cách giữa hai vị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
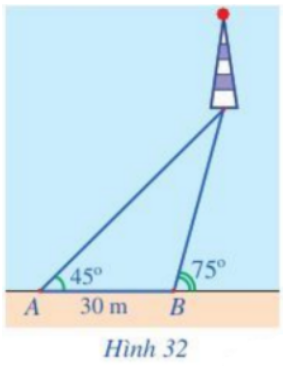
Phương pháp giải:
Gọi C là vị trí ngọn hải đăng, H là hình chiếu của C trên AB.
Bước 1: Tính góc ACB, ABC.
Bước 2: Tính AC bằng cách áp dụng định lí sin trong tam giác ABC:
Bước 3: Tính AH bằng công thức: AH = AC. cos A.
Lời giải:
Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.
Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.
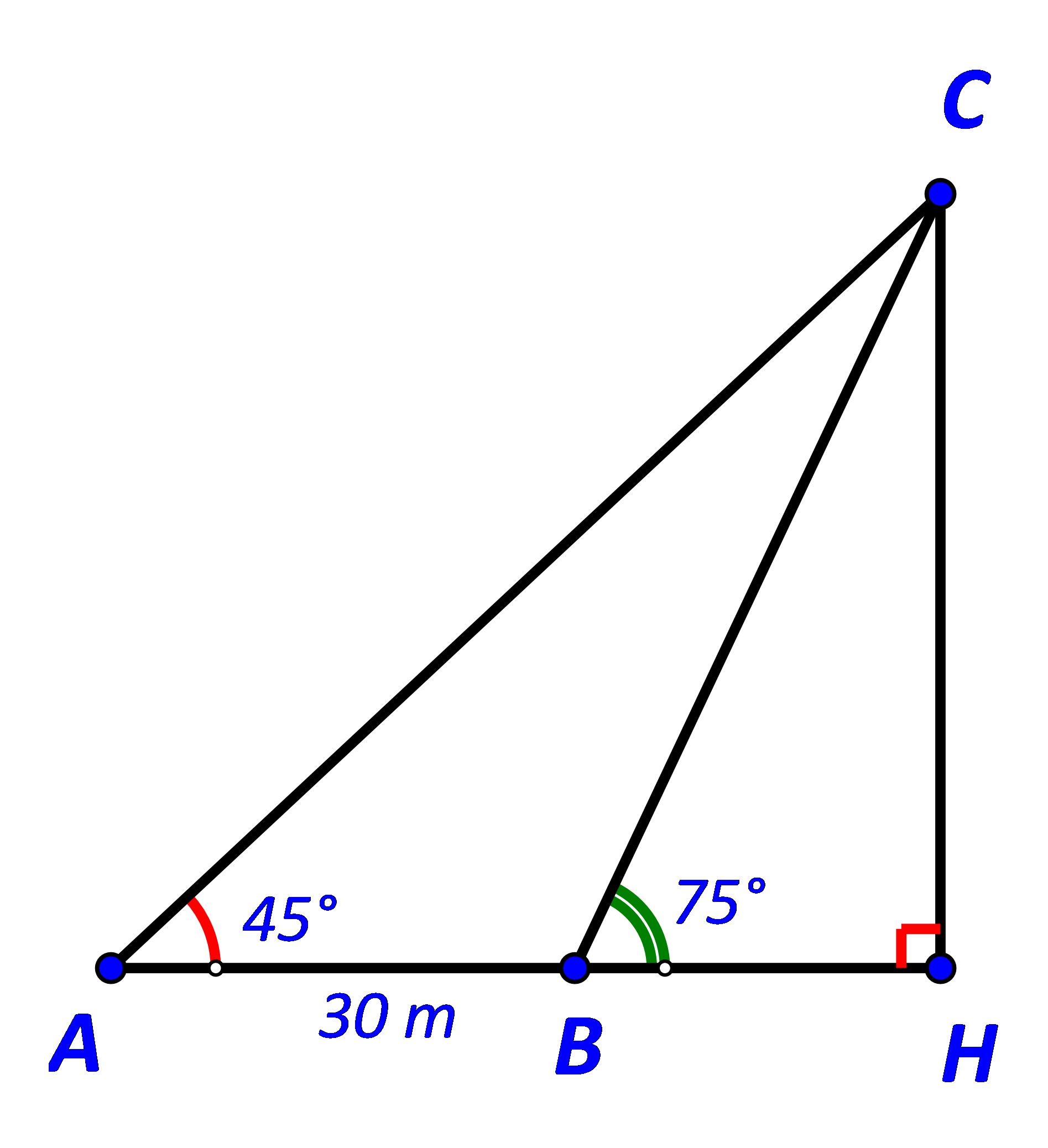
Ta có:
Áp dụng định lí sin trong tam giác ABC ta có:
Tam giác ACH vuông tại H nên ta có:
Vậy ngọn hải đăng cách bờ biển 56 m.
Bài tập vận dụng:
Bài 1. Một hành khách ngồi trong máy bay, bay ở độ cao 10 km nhìn xuống hai thị trấn dưới mặt đất. Góc hợp bởi phương ngang và hai thị trấn lần lượt là 28° và 55° (hình vẽ). Tính khoảng cách giữa hai thị trấn.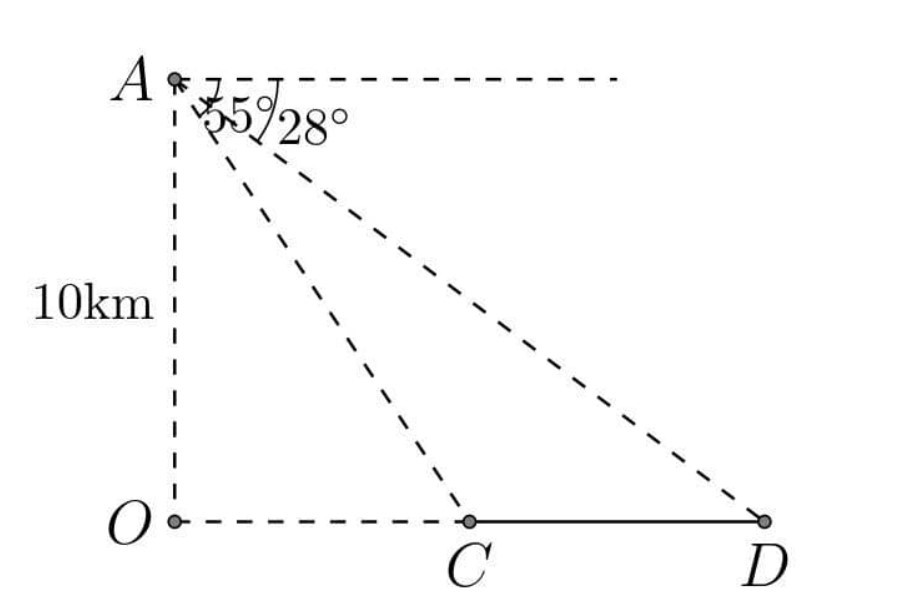
Hướng dẫn giải:
Đề bài yêu cầu chúng ta tính độ dài CD.
Ta có = 55° – 28° = 27°.
= 90° – 55° = 35°.
Và cos= . Do đó, AC = = ≈ 12,2km.
= 180° – – = 180° – 90° – 35° = 55°
Trong tam giác ACD có = 180° – = 125°
Và = 180° – (+) = 180° – (125° + 27°) = 28°.
Áp dụng định lí sin trong tam giác ACD, ta có:
⇔ CD = ≈ 11,79km.
Vậy khoảng cách giữa hai thị trấn là 11,79km.
Bài 2. Một cây cột điện cao 20 m được đóng trên một triền dốc thẳng nghiêng hợp với phương nằm ngang một góc 17°. Người ta nối một dây cáp từ đỉnh cột điện đến cuối dốc. Tính chiều dài của dây cáp biết rằng đoạn đường từ đáy cọc đến cuối dốc bằng 72 m (làm tròn đến chữ số thập phân thứ 2).
Hướng dẫn giải:
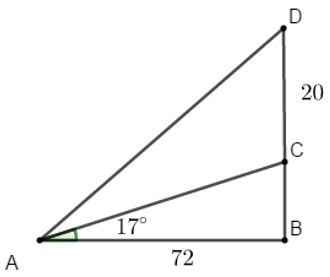
Bài toán được mô phỏng lại như hình vẽ với A, B lần lượt là điểm cuối dốc, chân của triền dốc; C, D lần lượt là chân và đỉnh của cây cột điện.
Suy ra chiều dài của dây cáp là đoạn AD.
Theo bài ra ta có: CD = 20 m, AB = 72 m, = 17°, = 90°.
= 180° – – = 180° – 17° – 90° = 73° (tổng ba góc một tam giác bằng 180°).
= 180° – = 180° – 73° = 107°
Tam giác ABC vuông tại B ⇒ AC = = ≈ 75,3 (m)
Áp dụng định lí côsin trong tam giác ACD, ta có:
AD2 = AC2 + CD2 – 2AC.CD.
= (75,3)2 + 202 – 2.75,3.20.cos107° ≈ 6950,7
AD = 83,4m
Vậy chiều dài của dây cáp là 83,4m.
Câu 1. Tam giác ABC có a = 21, b = 17, c = 10. Diện tích của tam giác ABC bằng:
A. ;
B. ;
C. ;
D. .
Hướng dẫn giải
Đáp án đúng là: D
Ta có:
Nửa chu vi của tam giác ABC là:
(đvđd).
Do đó
Diện tích tam giác ABC là:
(đvdt).
Xem thêm các bài giải Toán lớp 10 Cánh diều hay, chi tiết khác:
Hoạt động 1 trang 72 Toán lớp 10: Cho tam giác ABC có...
Hoạt động 2 trang 72 Toán lớp 10: Cho tam giác ABC có...
Hoạt động 3 trang 73 Toán lớp 10: Viết công thức định lí sin cho tam giác ABC....
Luyện tập vận dụng 1 trang 74 Toán lớp 10: Cho tam giác ABC có AB = 12;...
Luyện tập vận dụng 2 trang 76 Toán lớp 10: Từ trên nóc của một tòa nhà cao 18,5 m, bạn Nam quan sát một cái cây cách tòa nhà 30 m...
Bài 1 trang 77 Toán lớp 10: Cho tam giác ABC có...
Bài 2 trang 77 Toán lớp 10: Cho tam giác ABC có...
Bài 3 trang 77 Toán lớp 10: Cho tam giác ABC có...
Bài 4 trang 77 Toán lớp 10: Cho tam giác ABC có...
Bài 5 trang 77 Toán lớp 10: Tính độ dài cạnh AB trong mỗi trường hợp sau:...
Bài 6 trang 77 Toán lớp 10: Để tính khoảng cách giữa hai địa điểm A và B mà ta không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …),...
Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:
Bài 1: Giá trị lượng giác của một góc từ 0° đến 180°. Định lí côsin và định lí sin trong tam giác
Bài 2: Giải tam giác. Tính diện tích tam giác
Bài 4: Tổng và hiệu của hai vectơ
Bài 5: Tích của một số với một vectơ