Với giải Hoạt động 2 trang 72 Toán lớp 10 Cánh diều chi tiết trong Bài 2: Giải tam giác. Tính diện tích tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 2: Giải tam giác. Tính diện tích tam giác
Hoạt động 2 trang 72 Toán lớp 10: Cho tam giác ABC có . Viết công thức tính cos A.
Phương pháp giải:
Áp dụng định lí cosin cho tam giác ABC, từ đó suy ra công thức tính cos A.
Lời giải:
Áp dụng định lí cosin trong tam giác ABC ta có:
Chú ý:
Tương tự, ta suy ra công thức tính như sau:
Lý thuyết Giải tam giác
Như ta đã biết, một tam giác hoàn toàn xác định nếu biết một trong những dữ kiện sau:
– Biết độ dài hai cạnh và độ lớn góc xen giữa hai cạnh đó;
– Biết độ dài ba cạnh;
– Biết độ dài một cạnh và độ lớn hai góc kề với cạnh đó.
Giải tam giác là tính các cạnh và các góc của tam giác dựa trên những dữ kiện cho trước.
Ví dụ: Cho tam giác ABC có AB = 4, BC = 6, AC = . Điểm M thuộc đoạn BC sao cho MC = 2MB.
a) Tính cos các góc của tam giác ABC.
b) Tính độ dài cạnh AM.
Hướng dẫn giải:
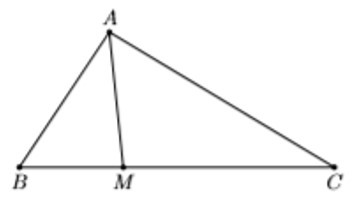
a) Theo định lí cosin trong tam giác ABC ta có:
cosB = = =
⇒ = 60°.
cosC = = =
cosA = = =
b) Ta có:
MC = 2MB ⇒ = ⇒ =
⇒ MB = BC = .6 = 2
Áp dụng định lí côsin trong tam giác AMB ta có:
AM2 = AB2 + BM2 – 2AB.BM.cosB = 42 + 22 – 2.4.2. = 12
⇒ AM = =
Ví dụ: Cho tam giác ABC có ; và cạnh AC = 15 cm. Tính các cạnh còn lại của tam giác ABC (làm tròn đến chữ số thập phân thứ 2).
Hướng dẫn giải:
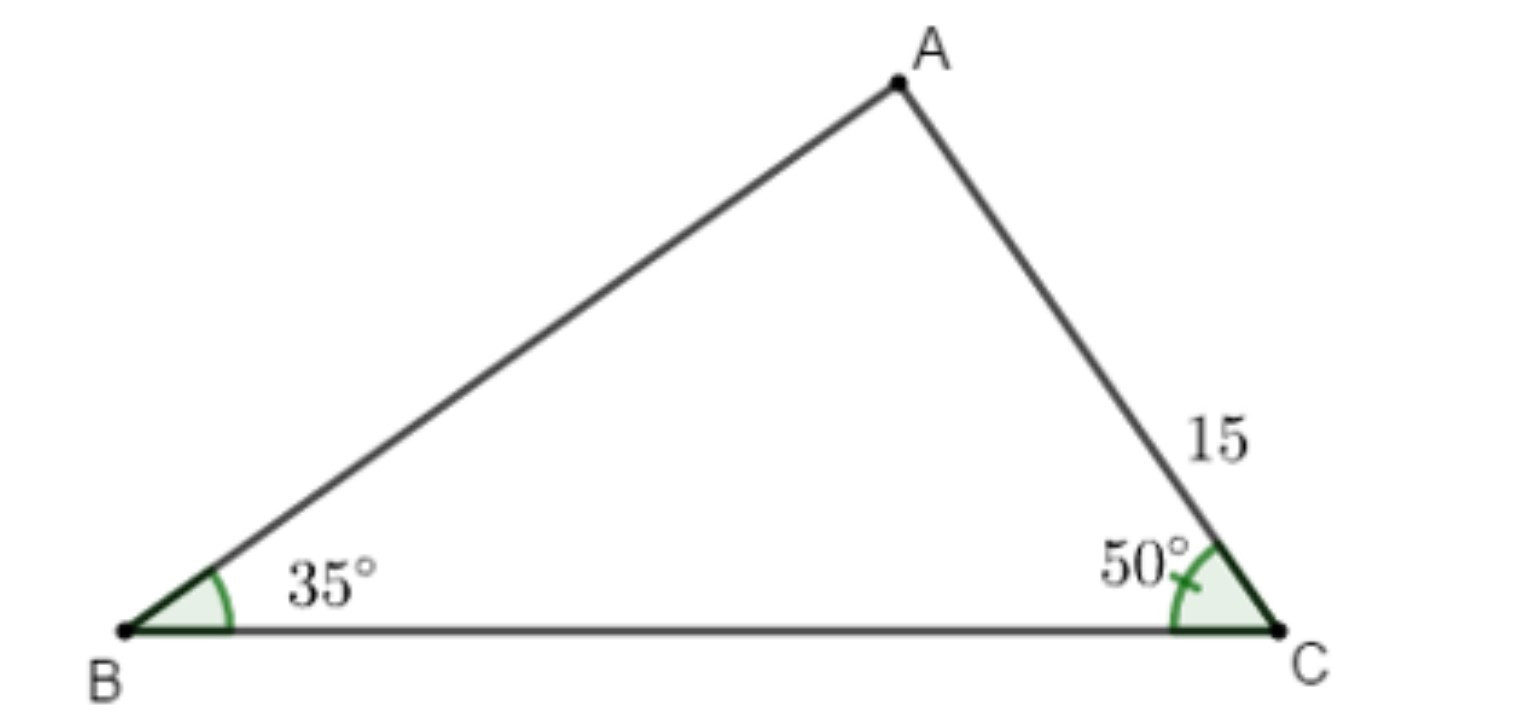
Ta có:
+ + = 180° (tổng ba góc trong tam giác)
Suy ra:
= 180° – – = 180° – 35° – 50° = 95°
Áp dụng định lí sin trong tam giác ABC ta có:
= =
Suy ra:
BC = = ≈ 26,05cm
AB = = ≈ 20,03cm
Vậy BC = 26,05cm và AB ≈ 20,03 cm.
Xem thêm các bài giải Toán lớp 10 Cánh diều hay, chi tiết khác:
Hoạt động 1 trang 72 Toán lớp 10: Cho tam giác ABC có...
Hoạt động 3 trang 73 Toán lớp 10: Viết công thức định lí sin cho tam giác ABC....
Luyện tập vận dụng 1 trang 74 Toán lớp 10: Cho tam giác ABC có AB = 12;...
Luyện tập vận dụng 2 trang 76 Toán lớp 10: Từ trên nóc của một tòa nhà cao 18,5 m, bạn Nam quan sát một cái cây cách tòa nhà 30 m...
Bài 1 trang 77 Toán lớp 10: Cho tam giác ABC có...
Bài 2 trang 77 Toán lớp 10: Cho tam giác ABC có...
Bài 3 trang 77 Toán lớp 10: Cho tam giác ABC có...
Bài 4 trang 77 Toán lớp 10: Cho tam giác ABC có...
Bài 5 trang 77 Toán lớp 10: Tính độ dài cạnh AB trong mỗi trường hợp sau:...
Bài 6 trang 77 Toán lớp 10: Để tính khoảng cách giữa hai địa điểm A và B mà ta không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …),...
Bài 7 trang 77 Toán lớp 10: Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là...
Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:
Bài 1: Giá trị lượng giác của một góc từ 0° đến 180°. Định lí côsin và định lí sin trong tam giác
Bài 2: Giải tam giác. Tính diện tích tam giác
Bài 4: Tổng và hiệu của hai vectơ
Bài 5: Tích của một số với một vectơ