Với giải Bài 5 trang 43 Toán lớp 10 Cánh diều chi tiết trong Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 2: Hàm số bậc hai và ứng dụng

Bài 5 trang 43 Toán lớp 10: Nêu khoảng đồng biến, khoảng nghịch biến của mỗi hàm số sau:

a) $y=5x^2+4x-1$

b) $y=-2x^2+8x+6$

Lời giải:

a) Hệ số $a=5>0,b=4\Rightarrow \frac{-b}{2a}=\frac{-4}{2.5}=\frac{-2}{5}$

Vậy hàm số nghịch biến trên khoảng $\left(-\mathrm{\infty };\frac{-2}{5}\right)$ và đồng biến trên $\left(\frac{-2}{5};+\mathrm{\infty }\right)$

b) Ta có $a=-2<0,b=8$

$\Rightarrow -\frac{b}{2a}=\frac{-8}{2.\left(-2\right)}=2$

Vậy hàm số đã cho đồng biến trên khoảng $\left(-\mathrm{\infty };2\right)$ và nghịch biến trên khoảng $\left(2;+\mathrm{\infty }\right)$

Bài tập vận dụng:

Bài 1. Xác định parabol y = ${\text{ax}}^2+\mathrm{b}\text{x}+4$ trong mỗi trường hợp sau:

a) Đi qua điểm M(1; 12) và N(–3; 4);

b) Có đỉnh là I(–3; –5).

Hướng dẫn giải

a) Thay x = 1; y = 12 vào phương trình y = ${\text{ax}}^2+\mathrm{b}\text{x}+4$ ta được:

12 = a. $1^2$+ b.1 + 4 = a + b = 8 (1)

Thay x = –3; y = 4 vào phương trình y = ${\text{ax}}^2+\mathrm{b}\text{x}+4$ ta được:

4 = a.${(-3)}^2$+ (–3).b + 4 = 9a – 3b = 0 (2)

Từ (1) và (2) ta có: $\left\{\begin{array}{l}\mathrm{a}+\mathrm{b}=8\\ 9\text{a}-3\mathrm{b}=0\end{array}\right.$$\iff$$\left\{\begin{array}{l}\mathrm{a}=2\\ \mathrm{b}=6\end{array}\right.$ . Như vậy y = ${\text{2x}}^2+6\text{x}+4$

b) Ta có: Toạ độ đỉnh I $\left(-\frac{\mathrm{b}}{2\text{a}};-\frac{\mathrm{\Delta }}{4\text{a}}\right)$= (–3; –5)

$\mathrm{\Delta }={\mathrm{b}}^2-4\text{a}\mathrm{c}$= ${\mathrm{b}}^2$ – 4.a.4 = ${\mathrm{b}}^2$ – 16a

$\left\{\begin{array}{l}-\frac{\mathrm{b}}{2\text{a}}=-3\\ -\frac{{\mathrm{b}}^2-16\text{a}}{4\text{a}}=-5\end{array}\right.$$\iff$$\left\{\begin{array}{l}\mathrm{b}-6\text{a}=0\\ {\mathrm{b}}^2-36\text{a}=0\end{array}\right.$$\iff$$\left\{\begin{array}{l}6\mathrm{b}-36\text{a}=0\\ {\mathrm{b}}^2-36\text{a}=0\end{array}\right.$$\iff$${\mathrm{b}}^2$– 6b = 0 $\iff$b(b – 6) = 0

$\iff$$\left[\begin{array}{l}\mathrm{b}=0\\ \mathrm{b}=6\end{array}\right.$$\iff$$\left[\begin{array}{l}\mathrm{a}=0\\ \mathrm{a}=1\end{array}\right.$. Như vậy trường a = 0; b = 0 không thoả mãn, ta chọn được:

a = 1; b = 6 ⇒ phương trình y = x² + 6x + 4.

Bài 2. Vẽ đồ thị của mỗi hàm số sau:

a) y = 2x² – 6x + 4;                   

b) y = –3x² – 6x – 3.

Hướng dẫn giải

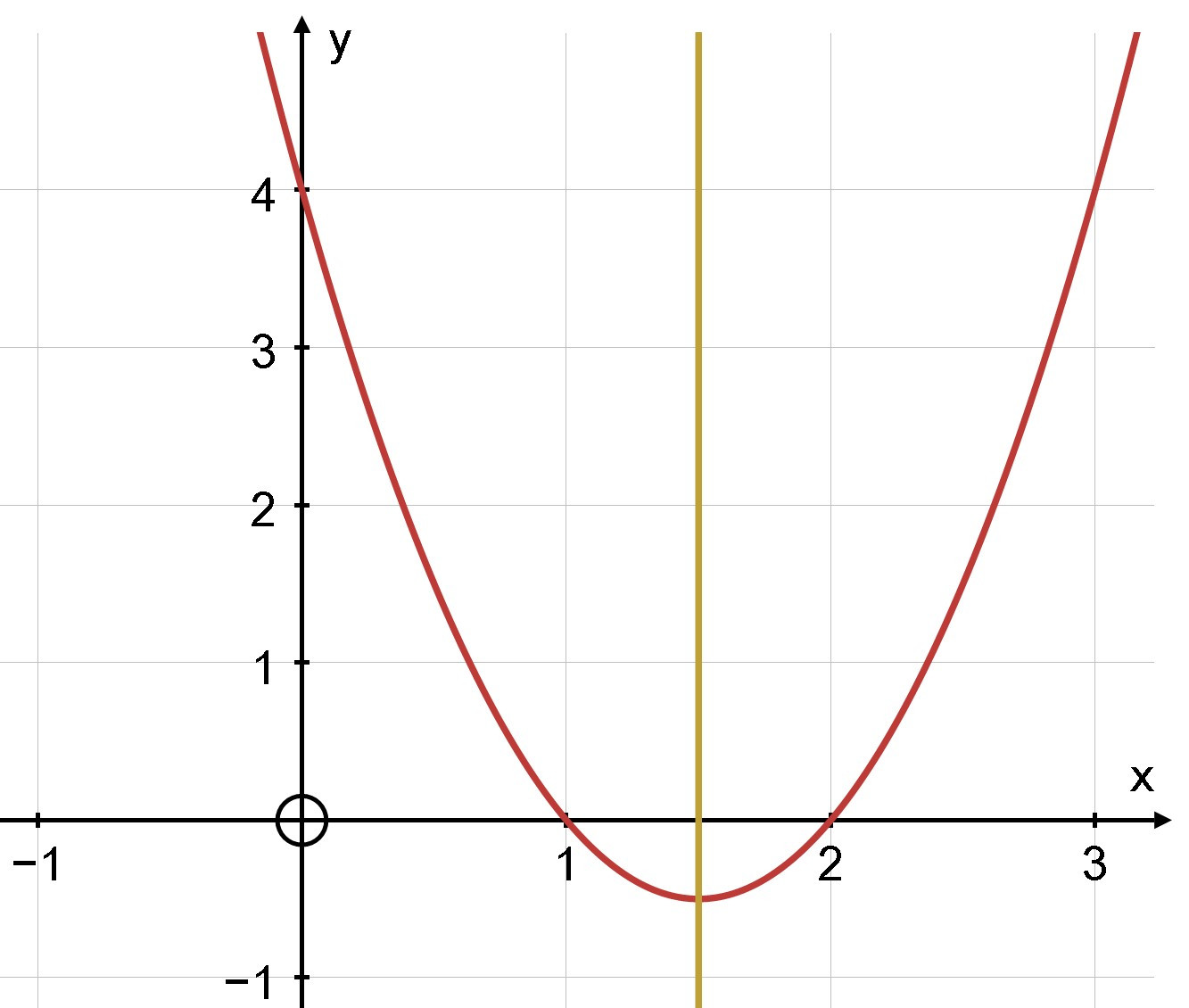
a)

– Tập xác định: D = ℝ

– Ta có: a = 2; b = –6; c = 4; $\mathrm{\Delta }={\mathrm{b}}^2-4\text{a}\mathrm{c}$ = (– 6)² – 4.2.4 = 4

– Toạ độ đỉnh I = $\left(-\frac{\mathrm{b}}{2\text{a}};-\frac{\mathrm{\Delta }}{4\text{a}}\right)$ = $\left(\frac{6}{2.2};\frac{-4}{4.2}\right)=\left(\frac{3}{2};-\frac{1}{2}\right)$

– Trục đối xứng $\mathrm{x}=-\frac{\mathrm{b}}{2\text{a}}$= $\frac{3}{2}$

– Giao điểm của parabol với trục Oy là A(0; 4)

– Giao điểm của parabol với trục Ox là B (1; 0); (2; 0)

– Chọn một điểm thuộc đồ thị cho x = –1 thay vào y = 2x² – 6x + 4 ta được điểm

D(–1; 12)

Vẽ parabol qua các điểm trên:

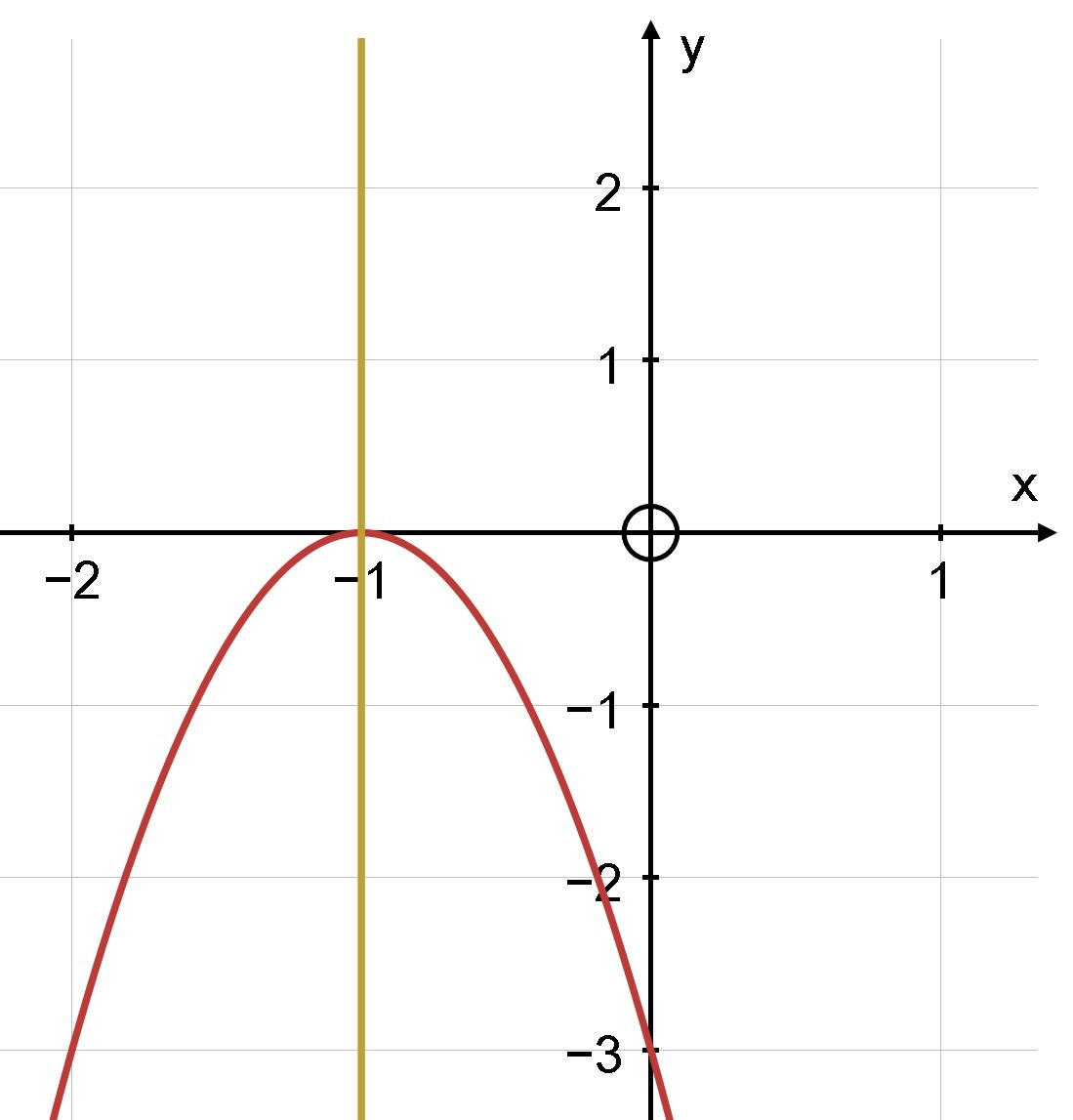
b)

– Tập xác định: D = ℝ

– Ta có: a = –3; b = –6; c = –3; $\mathrm{\Delta }={\mathrm{b}}^2-4\text{a}\mathrm{c}$ = (– 6)² – 4.(–3).(–3) = 0

– Toạ độ đỉnh I = $\left(-\frac{\mathrm{b}}{2\text{a}};-\frac{\mathrm{\Delta }}{4\text{a}}\right)$ = $\left(\frac{6}{2.(-3)};\frac{0}{4.(-3)}\right)=\left(-1;0\right)$

– Trục đối xứng $\mathrm{x}=-\frac{\mathrm{b}}{2\text{a}}$= –1

– Giao điểm của parabol với trục Oy là A(0; –3)

– Giao điểm của parabol với trục Ox là B (–1; 0)

– Chọn một điểm thuộc đồ thị cho x = 1 thay vào y = –3x² – 6x – 3 ta được điểm

D(1; –12)

– Chọn một điểm thuộc đồ thị cho x = –2 thay vào y = –3x² – 6x – 3 ta được điểm

D(–2; –3)

Vẽ parabol qua các điểm trên:

Câu 1. Cho hàm số $\mathrm{y}={\mathrm{ax}}^2+\mathrm{bx}+\mathrm{c}$$\left(\mathrm{a}\ne 0\right)$ có đồ thị như hình sau. Khẳng định nào sau đây đúng?

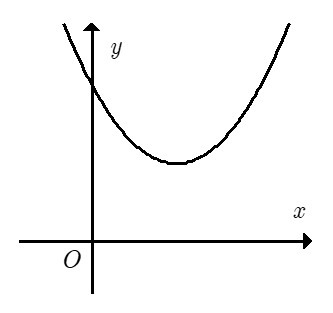
A. a > 0, b < 0, c < 0;

B. a > 0, b < 0, c > 0;

C. a > 0, b > 0, c > 0;

D. a < 0, b < 0, c > 0.

Hướng dẫn giải

Đáp án đúng là: B

Bề lõm hướng lên nên a > 0.

Hoành độ đỉnh parabol $\mathrm{x}=-\frac{\mathrm{b}}{2\mathrm{a}}>0$ nên b < 0.

Parabol cắt trục tung tại điểm có tung độ dương nên c > 0.

Xem thêm các bài giải Toán lớp 10 Cánh diều hay, chi tiết khác:

Câu hỏi khởi động trang 39 Toán lớp 10: Cầu cảng Sydney là một trong những hình ảnh biểu tượng của thành phố Sydney và nước Australia....

Hoạt động 1 trang 39 Toán lớp 10: Cho hàm số...

Luyện tập vận dụng 1 trang 39 Toán lớp 10: Cho hai ví dụ về hàm số bậc hai....

Hoạt động 2 trang 39 Toán lớp 10: Cho hàm số...

Hoạt động 3 trang 40 Toán lớp 10: Cho hàm số ...

Luyện tập vận dụng 2 trang 41 Toán lớp 10: Vẽ đồ thị mỗi hàm số bậc hai sau:...

Hoạt động 4 trang 41 Toán lớp 10: a) Quan sát đồ thị hàm số bậc hai ...

Luyện tập vận dụng 3 trang 42 Toán lớp 10: Lập bảng biến thiên của mỗi hàm số sau:...

Luyện tập vận dụng 4 trang 43 Toán lớp 10: Trong bài toán ở phần mở đầu, độ cao y (m) của một điểm thuộc vòng cung thành cầu cảng Sydney đạt giá trị lớn nhất là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?...

Bài 1 trang 43 Toán lớp 10: Trong các hàm số sau, hàm số nào là hàm số bậc hai?...

Bài 2 trang 43 Toán lớp 10: Xác định parabol...

Bài 3 trang 43 Toán lớp 10: Vẽ đồ thị của mỗi hàm số sau:...

Bài 4 trang 43 Toán lớp 10: Cho đồ thị hàm số bậc hai ở Hình 15.....

Bài 6 trang 43 Toán lớp 10: Khi du lịch đến thành phố St. Louis (Mỹ), ta sẽ thấy một cái cổng lớn có hình parabol hướng bề lõm xuống dưới, đó là cổng Arch.....

Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

Bài 3: Dấu của tam thức bậc hai

Bài 4: Bất phương trình bậc hai một ẩn

Bài 5: Hai dạng phương trình quy về phương trình bậc hai