Với giải HĐ3 trang 22 Toán lớp 10 Kết nối tri thức với cuộc sống trong Bài 3: Bất phương trình bậc nhất hai ẩn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 3: Bất phương trình bậc nhất hai ẩn
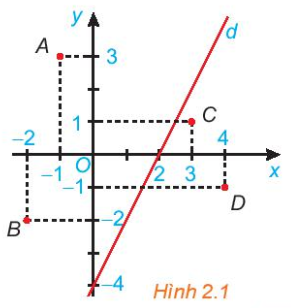
HĐ3 trang 22 Toán lớp 10: Cho đường thẳng d: 2x - y = 4 trên mặt phẳng toạ độ Oxy (H.2.1). Đường thẳng này chia mặt phẳng thành hai nửa mặt phẳng.
a) Các điểm 0,0; 0), A(-1; 3) và B(-2; -2) có thuộc cùng một nửa mặt phẳng bờ là đường thẳng d không?
Tính giá trị của biểu thức 2x - y tại các điểm đó và so sánh với 4.
b) Trả lời câu hỏi tương tự như câu a với các điểm C(3; 1), D(4; -1).
Phương pháp giải:
a)
Bước 1: Quan sát hình vẽ, nếu O, A, B nằm cùng một phía so với đường thẳng d thì 3 điểm đó cùng thuộc một nửa mặt phẳng bờ là đường thẳng d.
Bước 2: Thay tọa độ các điểm O, A, B vào biểu thức 2x-y và so sánh các giá trị tìm được với 4.
b)
Bước 1: Quan sát hình vẽ, nếu C, D nằm cùng một phía so với đường thẳng d thì 2 điểm đó cùng thuộc một nửa mặt phẳng bờ là đường thẳng d.
Bước 2: Thay tọa độ các điểm C, D vào biểu thức 2x-y và so sánh các giá trị tìm được với 4.
Lời giải:
a)
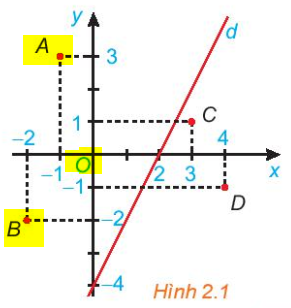
Bước 1:
Quan sát hình trên, các điểm A, O, B là các điểm được bôi vàng, và các điểm đó cùng nằm một phía (bên trái) nên chúng thuộc cùng một nửa mặt phẳng bờ là đường thẳng d.
Bước 2:
+) Thay tọa độ của điểm O(0;0) vào biểu thức 2x-y ta được: 2.0-0=0.
Như vậy giá trị của biểu thức 2x-y tại O là 0 và 0<4.
+) Thay tọa độ của điểm A(-1;3) vào biểu thức 2x-y ta được: 2.(-1)-3=-5.
Như vậy giá trị của biểu thức 2x-y tại A là -5 và -5<4
+) Thay tọa độ của điểm B(-2;-2) vào biểu thức 2x-y ta được: 2.(-2)-(-2)=-2.
Như vậy giá trị của biểu thức 2x-y tại B là -2 và -2<4.
b)
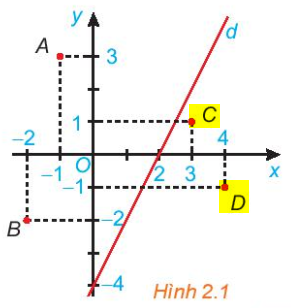
Bước 1:
Quan sát hình trên, các điểm C, D là các điểm được bôi vàng, và các điểm đó cùng nằm một phía (bên phải) nên chúng thuộc cùng một nửa mặt phẳng bờ là đường thẳng d.
Bước 2:
+) Thay tọa độ của điểm C(3;1) vào biểu thức 2x-y ta được: 2.3-1=5.
Như vậy giá trị của biểu thức 2x-y tại C là 5 và 5>4.
+) Thay tọa độ của điểm D(4;-1) vào biểu thức 2x-y ta được: 2.4-(-1)=9.
Như vậy giá trị của biểu thức 2x-y tại D là 9 và 9>4
Chú ý:
Khi thay tọa độ các điểm vào biểu thức 2x-y, nếu y là một giá trị âm thì cần đưa nguyên dấu vào trong biểu thức.
Lý thuyết Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ
- Trong mặt phẳng tọa độ Oxy, tập hợp các điểm có tọa độ là nghiệm của bất phương trình được gọi là miền nghiệm của bất phương trình đó.
- Người ta chứng minh được rằng đường thẳng d có phương trình chia mặt phẳng tọa độ Oxy thành 2 nửa mặt phẳng bờ d:
+ Một nửa mặt phẳng (không kể bờ d) gồm các điểm có tọa độ thỏa mãn ;
+ Một nửa mặt phẳng (không kể bờ d) gồm các điểm có tọa độ thỏa mãn ;
Bờ d gồm các điểm có tọa độ thỏa mãn .
- Cách biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn :
+ Vẽ đường thẳng trên mặt phẳng tọa độ Oxy.
+ Lấy một điểm không thuộc d.
+ Tính và so sánh với c.
+ Nếu thì nửa mặt phẳng bờ d chứa là miền nghiệm của bất phương trình. Nếu thì nửa mặt phẳng bờ d không chứa là miền nghiệm của bất phương trình.
Chú ý: Miền nghiệm của bất phương trình là miền nghiệm của bất phương trình bỏ đi đường thẳng và biểu diễn đường thẳng bằng nét đứt.
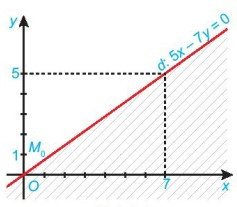
Ví dụ: Biểu diễn miền nghiệm của bất phương trình trên mặt phẳng tọa độ:
Bước 1: Vẽ đường thẳng trên mặt phẳng tọa độ Oxy.
Bước 2: Lấy điểm không thuộc d và thay x = 0 và y = 1 vào biểu thức ta được là mệnh đề đúng.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng bờ d chứa điểm (miền không bị gạch)
Xem thêm các bài giải Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:
Luyện tập 1 trang 23 Toán lớp 10: Cho bất phương trình bậc nhất hai ẩn ...
Luyện tập 2 trang 24 Toán lớp 10: Biểu diễn miền nghiệm của bất phương trình 2x+y...
Bài 2.1 trang 25 Toán lớp 10: Bất phương trình nào sau đây là bất phương tình bậc nhất hai ẩn?...
Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 3: Bất phương trình bậc nhất hai ẩn
Bài 4: Hệ bất phương trình bậc nhất hai ẩn
Bài 5: Giá trị lượng giác của một góc từ 0 đến 180