Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài 2: Tập hợp. Các phép toán trên tập hợp chi tiết sách Toán 10 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 2: Tập hợp. Các phép toán trên tập hợp
Video giải Toán 10 Bài 2: Tập hợp. Các phép toán trên tập hợp - Cánh diều
Lời giải:
Vì các học sinh tổ I đều là các học sinh lớp 10D nên tập hợp B là tập con của tập hợp A.
Kí hiệu:
I. Tập hợp
Lời giải:
Có hai cách cho một tập hợp:
+) Liệt kê các phần tử của tập hợp.
Chẳng hạn: A = {0; 1; 2; 3; 4; 5}
+) Chỉ ra tính chất đặc trưng của tập hợp đó.
Chẳng hạn: A = {}
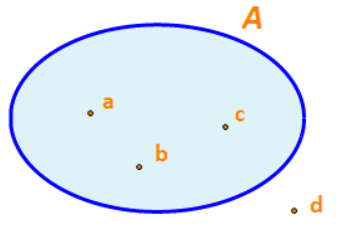
a) Viết tập hợp A trong Hình 1 bằng cách liệt kê các phần tử của các tập hợp đó.
b) Nêu phần tử không thuộc tập hợp A
Phương pháp giải:
a) Liệt kê các phần tử biểu thị bởi chấm bên trong vòng kín.
b) Xác định các phần tử không thuộc A (các chấm bên ngoài vòng kín)
Lời giải:
a) Tập hợp A là: A = {a; b; c}
b) Phần tử không thuộc tập hợp A là: d.
Hoạt động 3 trang 12 Toán lớp 10: Nêu số phần tử của mỗi tập hợp sau:
Phương pháp giải:
Viết lại tập hợp bằng cách liệt kê các phần tử, đếm số phần tử của tập hợp đó.
Lời giải:
. Tập hợp C không chứa phần tử nào vì bình phương mọi số thực đều không âm.
tập hợp D có duy nhất 1 phần tử là a.
tập hợp E có 3 phần tử.
: tập hợp N có vô số phần tử.
Luyện tập vận dụng 1 trang 13 Toán lớp 10: Nêu số phần tử của mỗi tập hợp sau:
Phương pháp giải:
Viết lại tập hợp bằng cách liệt kê các phần tử, đếm số phần tử của tập hợp đó.
Lời giải:
. Tập hợp G không chứa phần tử nào vì .
: tập hợp N* có vô số phần tử.
II. Tập con và tập hợp bằng nhau
Hoạt động 4 trang 13 Toán lớp 10: Cho hai tập hợp:
a) Viết tập hợp A, B bằng cách liệt kê các phần tử của tập hợp.
b) Mỗi phần tử của tập hợp A có thuộc tập hợp B không?
Lời giải:
a)
b) Mỗi phần tử của tập hợp A đều thuộc tập hợp B.
Luyện tập vận dụng 2 trang 13 Toán lớp 10: Cho hai tập hợp:
chia hết cho 3},
chia hết cho 9}.
Chứng tỏ rằng
Phương pháp giải:
Lấy một phần tử bất kì của tập hợp B, chứng minh phần tử đó thuộc A.
Lời giải:
Lấy n bất kì thuộc tập hợp B.
Ta có: n chia hết cho 9
Như vậy, mọi phần tử của tập hợp B đều là phần tử của tập hợp A hay
Hoạt động 5 trang 14 Toán lớp 10: Cho hai tập hợp:
là bội chung của 2 và 3},
là bội của 6}.
Các mệnh đề sau có đúng không?
a)
b)
Phương pháp giải:
a)
b)
Lời giải:
a) Nếu n là bội chung của 2 và 3 thì n là bội của 6, hay
Vậy mệnh đề đúng.
b) Nếu n là bội 6 thì n vừa là bội của 2 vừa là bội của 3.
Do đó n là bội chung của 2 và 3 hay .
Vậy mệnh đề đúng.
Luyện tập vận dụng 3 trang 14 Toán lớp 10: Cho hai tập hợp:
chia hết cho 3 và 4}, và chia hết cho 12}.
Chứng tỏ rằng E = G.
Phương pháp giải:
Ta chứng minh và .
Chỉ ra mọi phần tử của tập hợp E đều là phần tử của tập hợp G và ngược lại.
Lời giải:
Ta có:
n chia hết cho 3 và 4 n chia hết cho 12 (do (3,4) =1)
Do đó: nếu n là phần tử của tập hợp A thì n cũng là phần tử của tập hợp B và ngược lại.
Hay mọi phần tử của tập hợp A đều là phần tử của tập hợp B và ngược lại.
Vậy và hay E = G.
III. Giao của hai tập hợp
- Bóng đá gồm: An, Bình, Chung, Dũng, Minh, Nam, Phương.
- Bóng rổ gồm: An, Chung, Khang, Phong, Quang, Tuấn.
Hãy liệt kê danh sách các bạn đăng kí tham gia cả hai câu lạc bộ.
Lời giải:
Danh sách các bạn đăng kí tham gia cả hai câu lạc bộ là: An, Chung.
IV. Hợp của hai tập hợp
Hoạt động 7 trang 15 Toán lớp 10: Hai trường dự định tổ chức giải thi đấu thể thao cho học sinh lớp 10. Trường thứ nhất đề xuất ba môn thi đấu là: Bóng bàn, Bóng đá, Bóng rổ. Trường thứ hai đề xuất ba môn thi đấu là: Bóng đá, Bóng rổ, Cầu lông. Lập danh sách những môn thi đấu mà cả hai trường đã đề xuất.
Lời giải:
Danh sách những môn thi đấu mà cả hai trường đã đề xuất là: Bóng bàn, Bóng đá, Bóng rổ, Cầu lông.
Luyện tập vận dụng 4 trang 15 Toán lớp 10: Cho hai tập hợp:
Tìm
Phương pháp giải:
Lời giải:
V. Phần bù. Hiệu của hai tập hợp
Lời giải:
Tập hợp các số thực không phải là số vô tỉ chính là tập hợp các số hữu tỉ.
Hoạt động 9 trang 16 Toán lớp 10: Cho hai tập hợp: A = {2; 3; 5; 7; 14}, B = {3; 5; 7; 9; 11}.
Liệt kê các phần tử thuộc tập hợp A nhưng không thuộc tập hợp B.
Phương pháp giải:
Lần lượt kiểm tra mỗi phần tử của A xem phần tử đó có thuộc B hay không. Ghi lại các phần tử không thuộc tập hợp B.
Lời giải:
Các phần tử thuộc tập hợp A nhưng không thuộc tập hợp B là: 2; 14.
Luyện tập vận dụng 5 trang 16 Toán lớp 10: Cho hai tập hợp:
Tìm và .
Phương pháp giải:
Viết lại hai tập hợp dưới dạng liệt kê các phần tử.
Xác định và
Lời giải:
Ta có:
Và
Khi đó:
Tập hợp gồm các phần tử thuộc A mà không thuộc B. Vậy.
Tập hợp gồm các phần tử thuộc B mà không thuộc A. Vậy
Bài tập
Bài 1 trang 18 Toán lớp 10: Cho tập hợp . Viết tất cả các tập con của tập hợp X.
Phương pháp giải:
+) tập hợp rỗng:
+) Liệt kê các tập con chứa 1, 2 hoặc 3 phần tử của tập hợp X
Lời giải:
Các tập con của tập hợp X là:
+) tập hợp rỗng:
+) Các tập con chỉ chứa 1 phần tử của tập hợp X: {a}, {b}, {c}.
+) Các tập con chứa 2 phần tử của tập hợp X: {a; b}, {b; c}, {c; a}
+) Tập con chứa 3 phần tử của tập hợp X: là tập hợp X = {a; b; c}
Chú ý:
+) Mọi tập hợp X đều có 2 tập con là: và X.
Bài 2 trang 18 Toán lớp 10: Sắp xếp các tập hợp sau theo quan hệ "":
[2; 5], (2; 5), [2; 5), (1; 5].
Phương pháp giải:
Lời giải:
Bài 3 trang 18 Toán lớp 10: Xác định các tập hợp sau và biểu diễn chúng trên trục số:
a)
b)
c)
d)
Phương pháp giải:
Biểu diễn các tập hợp trên cùng 1 trục số.
Lời giải:
a) Đặt
Tập hợp A là khoảng (2; 5) và được biểu diễn là:

b) Đặt
Tập hợp B là khoảng và được biểu diễn là:

c) Đặt
Tập hợp C là nửa khoảng và được biểu diễn là:

d) Đặt
Tập hợp D là khoảng và được biểu diễn là:

Bài 4 trang 18 Toán lớp 10: Gọi A là tập nghiệm của phương trình ,
B là tập nghiệm của phương trình
Tìm .
Phương pháp giải:
Liệt kê các phần tử của A và B.
Lời giải:
Ta có:
Ta có:
Vậy .
a) và
b) và
Phương pháp giải:
Bước 1: Giải hai bất phương trình, xác định hai tập hợp E và G.
Bước 2: Xác định
Lời giải:
a) Ta có:
Tập hợp E là:
và
Tập hợp G là
{ và }
Vậy tập hợp D
Phương pháp giải:
+) Điều kiện xác định của biểu thức là:
Lời giải:
Ta có: A là tập nghiệm của đa thức P(x)
Để biểu thức xác định thì hay .
Gọi B là tập hợp các số thực x sao cho biểu thức xác định.
a) Có bao nhiêu học sinh ở lớp 10B tham gia câu lạc bộ thể thao và không tham gia câu lạc bộ âm nhạc?
b) Có bao nhiêu học sinh ở lớp 10B tham gia ít nhất một trong hai câu lạc bộ trên?
c) Biết lớp 10B có 40 học sinh. Có bao nhiêu học sinh không tham gia câu lạc bộ thể thao? Có bao nhiêu học sinh không tham gia cả hai câu lạc bộ?
Lời giải:
a) Trong 28 học sinh tham gia câu lạc bộ thể thao có 10 học sinh tham gia cả câu lạc bộ âm nhạc
Vậy có 28-10=18 học sinh chỉ tham gia câu lạc bộ thể thao và không tham gia câu lạc bộ âm nhạc
b) Số học sinh tham gia ít nhất một trong hai câu lạc bộ trên là: 28 + 19 – 10 = 37 (học sinh)
c) Cả lớp có 40 học sinh, trong đó có 28 học sinh tham gia câu lạc bộ thể thao.
Do đó số học sinh không tham gia câu lạc bộ thể thao là: 40 – 28 = 12 (học sinh)
Cả lớp có 40 học sinh, trong đó có 37 học sinh tham gia ít nhất một trong hai câu lạc bộ.
Vậy số học sinh không tham gia cả hai câu lạc bộ là: 40 – 37 = 3 (học sinh)
Bài 8 trang 18 Toán lớp 10: Một nhóm có 12 học sinh chuẩn bị cho hội diễn văn nghệ. Trong danh sách đăng kí tham gia tiết mục múa và tiết mục hát của nhóm đó, có 5 học sinh tham gia tiết mục múa, 3 học sinh tham gia cả hai tiết mục. Hỏi có bao nhiêu học sinh trong nhóm tham gia tiết mục hát? Biết có 4 học sinh của nhóm không tham gia tiết mục nào.
Lời giải:
Vì nhóm có 12 học sinh, trong đó có 4 học sinh không tham gia tiết mục nào nên tổng số học sinh tham gia hai tiết mục múa và hát là: 12 – 4 = 8 (học sinh)
Lại có: Trong 5 học sinh tham gia tiết mục múa, có 3 học sinh tham gia cả hai tiết mục
Vậy số học sinh chỉ tham gia tiết mục múa là: 5 – 3 = 2 (học sinh)
Do đó số học sinh tham gia tiết mục hát là: 8 – 2 = 6 (học sinh)
Vậy trong nhóm có 6 học sinh tham gia tiết mục hát.
Lý thuyết Hình hộp chữ nhật. Hình lập phương
1. Tập hợp
• Tập hợp (còn gọi là tập) là một khái niệm cơ bản trong toán học.
Để chỉ x là một phần tử của tập hợp A, ta viết x ∈ A (đọc là x thuộc A).
Để chỉ x không phải một phần tử của tập hợp A, ta viết x ∉ A (đọc là x không thuộc A).
• Biểu diễn tập hợp bằng một trong 2 cách:
+ Liệt kê các phần tử của tập hợp.
+ Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
Ví dụ: Biểu diễn tập hợp B gồm các số tự nhiên có một chữ số và chia hết cho 3.
+ Liệt kê các phần tử: B = {0; 3; 6; 9}
+ Chỉ ra tính chất đặc trưng của các phần tử: B = {x ∈ ℕ | 0 ≤ x ≤ 9 và x ⁝ 3}
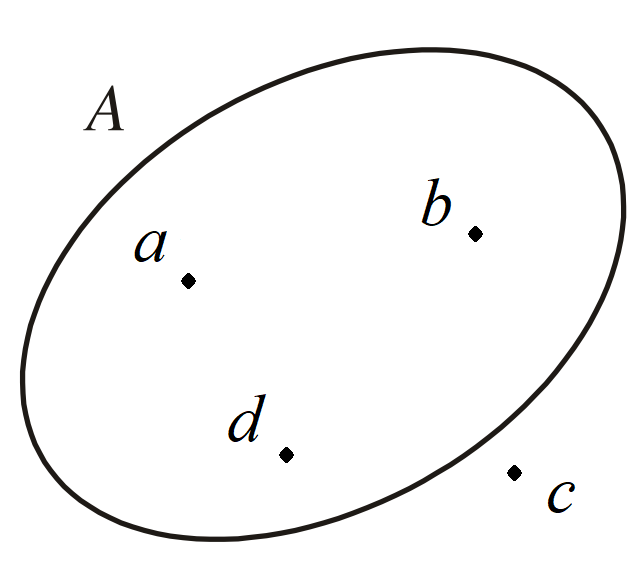
• Minh hoạ tập hợp bằng biểu đồ Ven. Mỗi phần tử thuộc tập hợp được biểu diễn bởi một chấm bên trong vòng kín, còn phần tử không thuộc tập hợp được biểu diễn bởi một chấm bên ngoài vòng kín.
Ở hình dưới, các phần tử thuộc tập hợp A là a, b, d; phần tử không thuộc tập hợp A là c.
• Một tập hợp có thể không có phần tử nào, có một phần tử, có nhiều phần tử, có vô số phần tử. Tập hợp không chứa phần tử nào được gọi là tập hợp rỗng, kí hiệu là .
Chú ý: Khi C là tập hợp rỗng, ta viết C =, không được viết .
2. Tập hợp con và tập hợp bằng nhau
• Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập con của tập B, kí hiệu là A ⊂ B. Ta còn đọc là A chứa trong B.
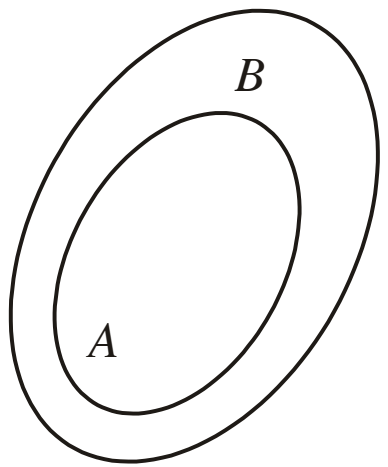
Quy ước: Tập hợp rỗng là tập con của mọi tập hợp.
+ A ⊂ B ⇔ (∀x, x ∈ A ⇒ x ∈ B).
+ Khi A ⊂ B, ta cũng viết B ⊃ A, đọc là B chứa A.
+ Nếu A không phải tập con của B, ta viết A ⊄ B.
Ví dụ: Cho hai tập hợp A = {n ∈ ℕ | n ⁝ 9} và B = {n ∈ ℕ | n ⁝ 3}. Chứng minh A ⊂ B.
Hướng dẫn giải
Với mọi số tự nhiên n ∈ A thì n chia hết cho 9
⇒ n = 9k = 3.(3k) (k ∈ ℕ)
⇒ n cũng chia hết cho 3, tức là n ∈ B.
Do đó A ⊂ B.
+ A ⊂ A với mọi tập hợp A.
+ Nếu A ⊂ B và B ⊂ C thì A ⊂ C.
• Khi A ⊂ B và B ⊂ A thì ta nói hai tập hợp A và B bằng nhau, viết là A = B.
Ví dụ: Cho tập hợp C gồm các tứ giác có 4 cạnh bằng nhau và tập hợp D gồm các hình thoi. Ta thấy:
+ Mọi tứ giác có 4 cạnh bằng nhau đều là hình thoi, tức là C ⊂ D.
+ Ngược lại, mọi hình thoi đều có 4 cạnh bằng nhau, tức là D ⊂ C.
Do đó hai tập hợp C và D bằng nhau.
3. Giao của hai tập hợp:
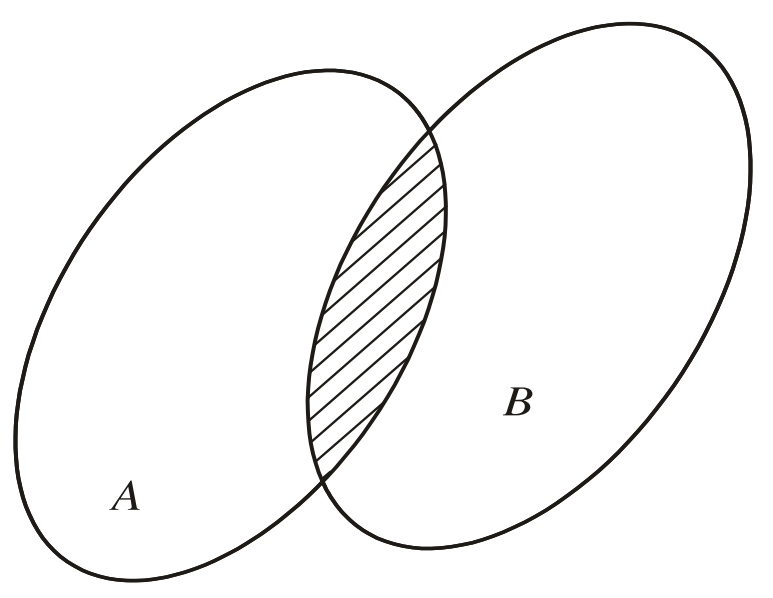
• Tập hợp gồm tất cả các phần tử vừa thuộc A vừa thuộc B được gọi là giao của A và B, kí hiệu A ∩ B.
Vậy A ∩ B = {x | x ∈ A và x ∈ B}.
Tập hợp A ∩ B được minh hoạ bởi phần gạch chéo trong hình dưới.
Ví dụ:
Tìm giao của tập hợp A = {x ∈ ℕ | 18 ⁝ x} và B = {x ∈ ℕ | 30 ⁝ x}
Hướng dẫn giải
Tập hợp A gồm các số tự nhiên thỏa mãn là ước của 18. Khi đó A = {1; 2; 3; 6; 9; 18}.
Tập hợp B gồm các số tự nhiên thỏa mãn là ước của 30. Khi đó B = {1; 2; 3; 5; 6; 10; 15; 30}.
Vậy A ∩ B = {1; 2; 3; 6}.
4. Hợp của hai tập hợp
• Tập hợp gồm tất cả các phần tử thuộc A hoặc thuộc B được gọi là hợp của A và B, kí hiệu A ∪ B.
Vậy A ∪ B = {x | x ∈ A và x ∈ B}.
Tập hợp A ∩ B được minh hoạ bởi phần gạch chéo trong hình dưới.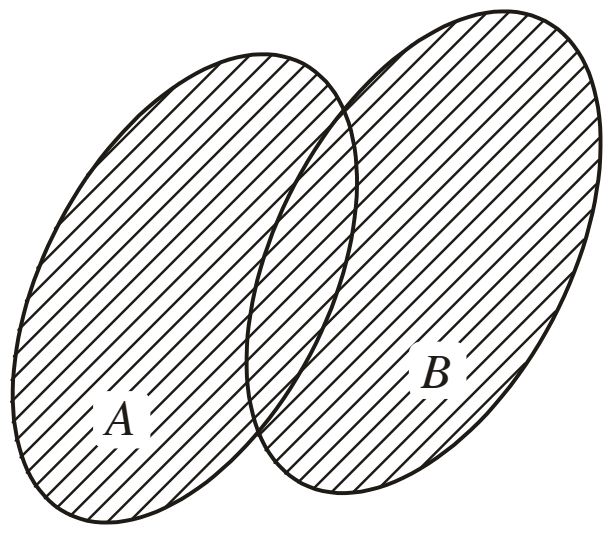
Ví dụ: Tìm hợp của tập hợp A = {x ∈ ℕ | 18 ⁝ x} và B = {x ∈ ℕ | 30 ⁝ x}
Hướng dẫn giải
Tập hợp A gồm các số tự nhiên thỏa mãn là ước của 18. Khi đó A = {1; 2; 3; 6; 9; 18}.
Tập hợp B gồm các số tự nhiên thỏa mãn là ước của 30. Khi đó B = {1; 2; 3; 5; 6; 10; 15; 30}.
Vậy A ∪ B = {1; 2; 3; 5; 6; 9; 10; 15; 18; 30}.
5. Phần bù và hiệu của hai tập hợp:
• Cho A ⊂ B. Tập hợp những phần tử của B mà không phải phần tử của A được gọi là phần bù của A trong B, kí hiệu CBA.
Vậy, khi A ⊂ B ta có CBA = {x | x ∉ A và x ∈ B}.
Tập hợp CBA được mô tả bằng phần gạch chéo trong hình dưới.
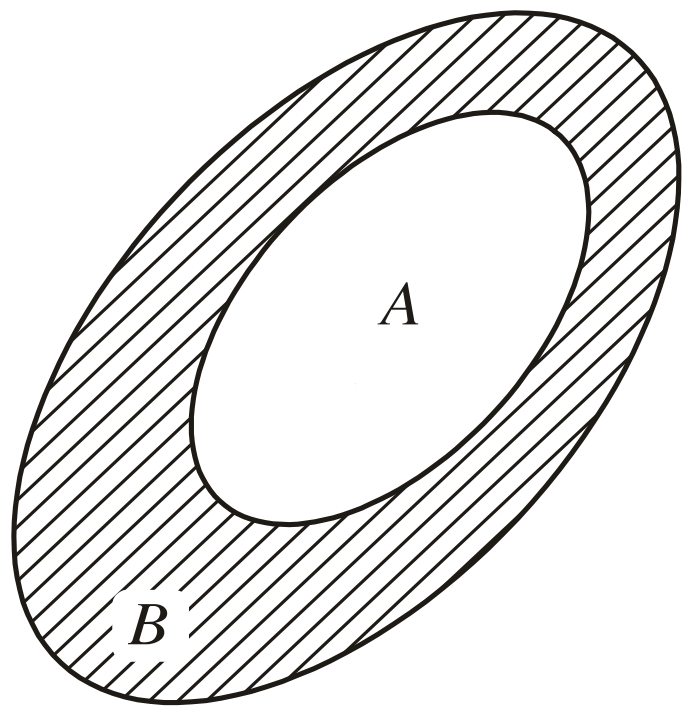
Ví dụ: Tìm phần bù của tập hợp A = {x ∈ ℕ | 10 ⁝ x} và B = {x ∈ ℕ | 30 ⁝ x}
Hướng dẫn giải
Tập hợp A là tập các số tự nhiên thỏa mãn là ước của 10. Khi đó A = {1; 2; 5; 10}.
Tập hợp B là tập các số tự nhiên thỏa mãn là ước của 30. Khi đó B = {1; 2; 3; 5; 6; 10; 15; 30}
Vậy CBA = {3; 6; 15; 30}.
• Tập hợp gồm các phần tử thuộc A nhưng không thuộc B được gọi là hiệu của A và B, kí hiệu A \ B.
Vậy A \ B = {x | x ∈ A và x ∉ B}.
Tập hợp A \ B được minh hoạ bởi phần gạch chéo trong hình dưới.
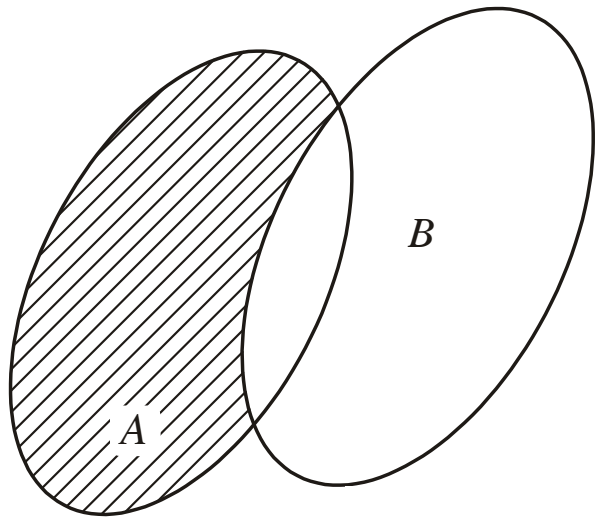
Ví dụ: Tìm phần bù của tập hợp A = {x ∈ ℕ | 20 ⁝ x} và B = {x ∈ ℕ | 30 ⁝ x}
Hướng dẫn giải
Tập hợp A là tập các số tự nhiên thỏa mãn là ước của 20. Khi đó A = {1; 2; 4; 5; 10; 20}.
Tập hợp B là tập các số tự nhiên thỏa mãn là ước của 30. Khi đó B = {1; 2; 3; 5; 6; 10; 15; 30}.
Vậy A \ B = {4; 20}.
• Các tập hợp ℕ, ℤ, ℚ, ℝ lần lượt là tập hợp số tự nhiên, tập hợp số nguyên, tập hợp số hữu tỉ, tập hợp số thực.
Ta có quan hệ sau: ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ.
• Một số tập con thường dùng của tập số thực:
|
Tập hợp |
Tên gọi và kí hiệu |
Biểu diễn trên trục số |
|
ℝ |
Tập hợp số thực (−∞; +∞) |
|
|
{x ∈ ℝ | a ≤ x ≤ b} |
Đoạn [a; b] |
|
|
{x ∈ ℝ | a < x < b} |
Khoảng (a; b) |
|
|
{x ∈ ℝ | x > a} |
Khoảng (a; +∞) |
|
|
{x ∈ ℝ | x < b} |
Khoảng (−∞; b) |
|
|
{x ∈ ℝ | a ≤ x < b} |
Nửa khoảng [a; b) |
|
|
{x ∈ ℝ | a < x ≤ b} |
Nửa khoảng (a; b] |
|
|
{x ∈ ℝ | x ≥ a} |
Nửa khoảng [a; +∞) |
|
|
{x ∈ ℝ | x ≤ b} |
Nửa khoảng (−∞; b] |
|
Kí hiệu −∞ đọc là âm vô cực (âm vô cùng), kí hiệu +∞ đọc là dương vô cực (dương vô cùng), a và b là các đầu mút của các đoạn, khoảng, nửa khoảng.
Ví dụ: Đọc tên, kí hiệu và biểu diễn mỗi tập hợp sau trên trục số:
a) A = {x ∈ ℝ | −1 ≤ x < 2};
b) B = {x ∈ ℝ | 3x − 4 < 0}.
Hướng dẫn giải
a) Tập A là nửa khoảng [−1; 2) và được biểu diễn là:
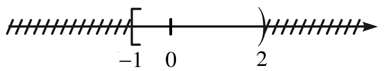
b) Ta có: 3x − 4 < 0 ⇔ x < .
Tập B là khoảng và được biểu diễn là:
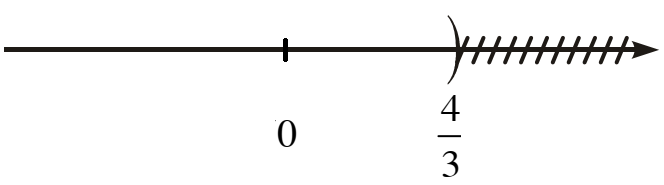
Bài giảng Toán 10 Bài 2: Tập hợp. Các phép toán trên tập hợp - Cánh diều
Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:
Bài 1: Bất phương trình bậc nhất hai ẩn
Bài 2: Hệ bất phương trình bậc nhất hai ẩn