Đồ thị của hàm số y = f(x) đi qua ba điểm có toa độ là (0;

Đồ thị của hàm số y = f(x) đi qua ba điểm có toa độ là (0; –2), (2; 6) và (3; 13)

Với giải ý b Bài 8 trang 10 SBT Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài 1: Dấu của tam thức bậc hai giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải sách bài tập Toán lớp 10 Bài 1: Dấu của tam thức bậc hai

Bài 8 trang 10 SBT Toán 10 Tập 2: Xác định giá trị của các hệ số a, b, c và xét dấu của tam thức bậc hai $f (x) {=ax}^{2} + b x + c$ trong mỗi trường hợp sau:

b) Đồ thị của hàm số y = f(x) đi qua ba điểm có toa độ là (0; –2), (2; 6) và (3; 13);

c) f(– 5) = 33, f (0) = 3 và f(2) = l9.

Lời giải:

b) Ta có:

Đồ thị của hàm số $y = f (x)$ đi qua điểm có toạ độ là (0; – 2) nên –2 = c (1)

Đồ thị của hàm số $y = f (x)$ đi qua ba điểm có toạ độ là (2; 6) nên 6 = 4a + 2b + c (2)

Đồ thị của hàm số $y = f (x)$ đi qua ba điểm có toạ độ là (3; 13) nên 13 = 9a + 3b + c (3).

Thay (1) vào phương trình (2) và (3) ta có:

$\{\begin{cases} 4a + 2 b = 8 \\ 9a + 3 b = 15 \end{cases} \Leftrightarrow \{\begin{cases} 2a + b = 4 \\ 3a + b = 5 \end{cases} \Leftrightarrow \{\begin{cases} a = 1 \\ 3.1 + b = 5 \end{cases} \Leftrightarrow \{\begin{cases} a = 1 \\ b = 2 \end{cases}$

Do đó f (x) = x² + 2x – 2.

Xét f ( x ) = x² + 2x – 2 có ∆ = 2² – 4.( –2 ).1 = 12 nên f ( x ) có hai nghiệm phân biệt lần lượt là:

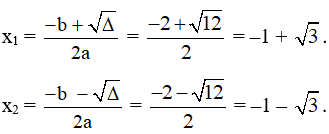
Sách bài tập Toán 10 Bài 1: Dấu của tam thức bậc hai - Chân trời sáng tạo (ảnh 1)

Như vậy, f (x) có a = 1 > 0, ∆ > 0 và có hai nghiệm x₁ = –1 + $\sqrt{3}$ , x₂ = –1 – $\sqrt{3}$ nên:

f (x) âm trong khoảng ( –1 – $\sqrt{3}$ ; –1 + $\sqrt{3}$ ).

f (x) dương trong khoảng Sách bài tập Toán 10 Bài 1: Dấu của tam thức bậc hai - Chân trời sáng tạo (ảnh 1)

c) Ta có:

f(– 5) = 33 nên 33 = 25a – 5b + c (1)

f (0) = 3 nên 3 = c (2)

f(2) = 19 nên 19 = 4a + 2b + c (3)

Thay (2) vào phương trình (1) và (3) ta có $\{\begin{cases} 25 a - 5 b = 30 \\ 4a + 2 b = 16 \end{cases}$ . Giải hệ phương trình ta được a = 2 và b = 4.