Với giải Bài 4.34 trang 65 SBT Toán lớp 7 Kết nối tri thức chi tiết trong Bài 15: Các trường hợp bằng nhau của tam giác vuông giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải sách bài tập Toán lớp 7 Bài 15: Các trường hợp bằng nhau của tam giác vuông
Bài 4.34 trang 65 SBT Toán 7 Tập 1: Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm của AB và AD (H.4.36). Chứng minh rằng BN = CM và BN ⊥ CM.
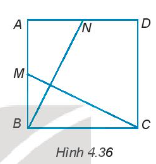
Hướng dẫn giải
Vì ABCD là hình vuông nên AB = BC = CD = DA.
Vì N là trung điểm của AD nên AN = ND = .
Vì M là trung điểm của AB nên AM = MB = .
Mà AB = AD nên AN = BM.
Xét ∆ANB và ∆BMC có:
AN = BM (chứng minh trên)
AB = BC (chứng minh trên)
= = 90° (do ABCD là hình vuông)
Do đó, ∆ANB = ∆BMC (hai cạnh góc vuông)
Suy ra, BN = CM (hai cạnh tương ứng).
Gọi E là giao điểm của BN và CM.
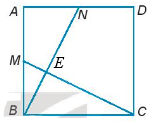
Do ∆ANB = ∆BMC nên .
Từ định lí tổng ba góc trong tam giác BME và tam giác ABN, ta suy ra:
.
Vậy BN vuông góc với CM tại E.
Xem thêm các bài giải SBT Toán 7 Kết nối tri thức hay, chi tiết khác:
Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác
Bài 15: Các trường hợp bằng nhau của tam giác vuông
Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
Bài 17: Thu thập và phân loại dữ liệu
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
